1.8 Successions i progressions
Una successió és una llista,
possiblement infinita, de nombres reals, cada un dels quals ocupa un lloc
en la successió a partir del lloc 1. Els nombres que apareixen en
una successió s'anomenen els seus termes.
El terme de posició n s'escriu an
i la successió com un tot s'escriu { an }.
Hi ha dos procediments principals de definir una
successió:
* donar una fórmula que per a cada n produeixi
an. Aquesta fórmula és el terme general
de la successió.
* donar una regla de construcció que relacioni
un terme amb els anteriors i permeti obtenir-lo a partir d'ells. Aquesta
regla que expressa an a partir d'an-1, an-2,
etc. és una relació de recurrència.
Coneixent una relació de recurrència i el terme o els termes inicials es poden obtenir d'un en un tots els termes.
Les successions més corrents a les ciències naturals o socials són les formades pels valors d'una magnitud que varia amb el temps, i que es prenen al cap de 1, 2, 3, ... intervals de temps iguals.
La successió més important a les matemàtiques
és la que té per terme general an =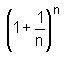 
.
Els seus termes s'estabilitzen al voltant de e = 2,71828...
Un tipus especial de successions són les progressions.
Una successió és una progressió aritmètica si ve definida per una relació de recurrència de la forma an = an-1 +d, on d és constant (positiva o negativa) i s’anomena la diferència de la progressió.
El terme general d'una progressió aritmètica és an = a1+(n-1)d
La suma dels termes d'una progressió aritmètica
compresos entre els llocs 1 i n rep el nom de suma parcial de lloc
n i es designa per Sn. Es calcula fent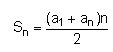 
El càlcul d'un nombre determinat de termes
situats entre dos de donats d’una progressió aritmètica s’anomena
interpolació
lineal.
Per interpolar n termes entre a i b (a <
b), de manera que formin progressió aritmètica, hem de calcular
la diferència, que serà d=
i després anar afegint aquesta quantitat al més petit dels
dos nombres donats.
Una successió és una progressió geomètrica si ve definida per una relació de recurrència de la forma an = an-·r, on r és constant i s'anomena la raó de la progressió.
El terme general d'una progressió geomètrica és an = a1·rn-1
La suma dels termes d'una progressió geomètrica
compresos entre els llocs 1 i n rep el nom de suma parcial de lloc
n i es designa per Sn. Es calcula fent 
Quan la raó és un nombre menor de
la unitat, la progressió geomètrica és decreixent
i aleshores es pot trobar el valor al qual s’acosta tant com es vulgui
la suma de tots els seus termes, que seria: 
Les progressions geomètriques més
importants són les formades pels valors d'una magnitud que varia
amb ritme constant durant successius períodes de temps. Si el valor
inicial és a1 i en cada període augmenta p%, el
valor al cap de n períodes és el que correspon a una progressió
geomètrica de raó 1+p/100: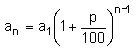 
