Exercicis d'Àlgebra

2.4 Funcions racionals

Els exercicis els has de respondre en suport paper.

25. Simplifica aquestes fraccions algebraiques: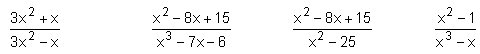 

26. Fes aquestes operacions amb fraccions algebraiques i deixa el resultat simplificat:

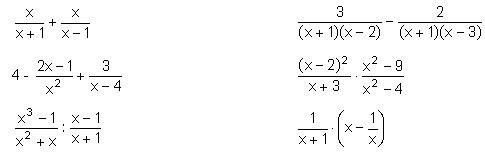
Pots comprovar els resultats amb Wiris.

27. Resol les equacions racionals: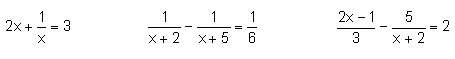 

28. Resol (amb Graphmatica) per superposició de dos gràfics l'equació   . Busca'n les tres solucions.

29. Calcula el domini de les funcions racionals: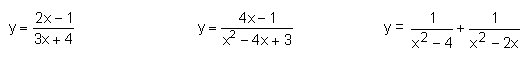 

TREBALL ESPECIAL
 

30. Aquest treball tracta de les funcions homogràfiques, que són les que tenen una fórmula com  Depenen, doncs, de 4 paràmetres a, b, c, d. Les seves gràfiques s'anomenen hipèrboles. A partir d'ara i en aquest enunciat escriurem les fórmules "en horitzontal" o sigui y=(ax+b)/(cx+d)

1. Les asímptotes Dibuixa amb Graphmatica el gràfic de y = (x+2)/(x-4) . Afegeix-li les rectes y = 1, x = 4.  Aquestes rectes "emmarquen" el gràfic, que no les arriba a tocar mai. S'anomenen asímptotes de la funció (asímptota horitzontal i asímptota vertical). Dibuixa el gràfic de vàries funcions y = (x+b)/(x+d)  amb b i d positius o negatius. Veuràs que totes tenen la mateixa asímptota horitzontal. Intenta, però, descobrir quina és la posició de l'asímptota vertical. Té relació amb b? Té relació amb d? Dibuixa el gràfic de y = (4x-1)/(2x-6). Afegeix-li les asímptotes. Sabries endevinar, només amb la fórmula, perquè l'asímptota vertical és la que és? Comprova la teva idea posant-te a tu mateix exemples de la forma y = (x+b)/(cx+d), amb b, c i d positius o negatius. Té relació amb b? Té relació amb c? Té relació amb d? Suposem que ja saps descobrir l'asímptota vertical i passem a l'horitzontal. Torna a y = (4x-1)/(2x-6). Posa-li l'asímptota horitzontal. Ara varia una mica: prova les y = (4x+b)/(2x+d), per a diferents b i d positius o negatius. Què passa amb l'asímptota horitzontal? Prova ara les y = (6x+b)/(2x+d). Ja tens alguna idea d'on es posa l'asímptota horitzontal? Si no la tens, segueix fent proves. Si ja la tens, comprova que la teva idea sigui correcta amb més exemples.

2. La posició respecte les asímptotes Les asímptotes divideixen l'espai en quatre quadrants. Alguns gràfics ocupen el primer i el tercer; els direm "gràfics 1-3" i alguns ocupen el segon i el quart; són els "gràfics 2-4". Es tracta de que, després de posar-te molts exemples, descobreixis, a partir de la fórmula, de quin dels dos tipus serà el gràfic. Prova si sempre són del mateix tipus: 1. les y = 1(x+d) , variant d  2. les y = b/x , variant b 3. les y = 1/(cx+d), variant c i d 4. les y = b/(x+d) , variant b i d 5. les y = ax/(x+d) , variant a i d 6. les y = (ax+b)/(x+d), variant a, b i d .... En cada cas, "variant" significa anar provant valors positius i negatius. Veuràs que el tipus depèn del signe, positiu o negatiu, d'un dels paràmetres (casos 2, 3, 4) o de dos d'ells (cas 5).  El cas 6 és més complicat. Veuràs que encara que en facis proves amb els tres paràmetres positius, a vegades serà d'un tipus i a vegades d'un altre. De què depèn, doncs?. Una pista: mira si b és més gran o més petit que el producte a·d. REDACTA ARA TOT ALLÒ QUE HAGIS DESCOBERT I TOTES LES CONCLUSIONS A QUÈ HAGIS ARRIBAT.