1.6 Sèries dobles
Són les sèries formades per l'observació
de dues característiques numèriques dels individus d'un conjunt.
Habitualment aquestes sèries es presenten
en forma de taules de tres columnes:
1. Individus (a vegades s'ometen)
2. Valors de la primera variable (x)
3. Valors de la segona variable (y)
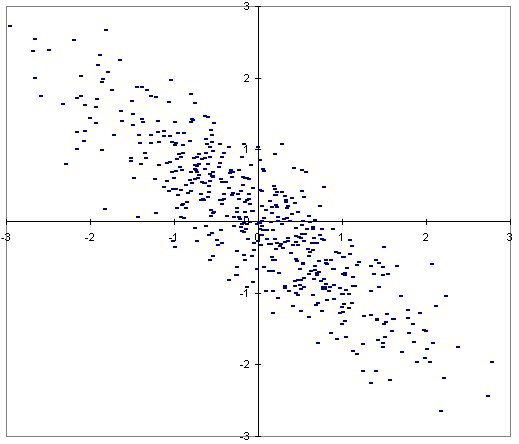
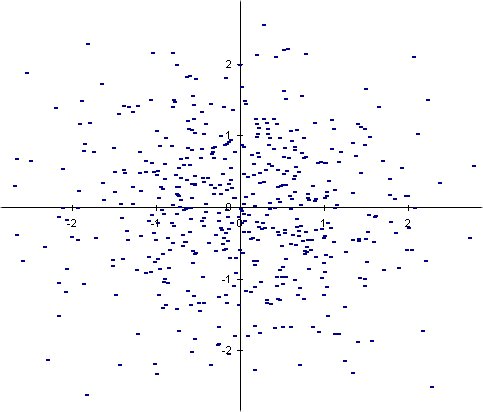
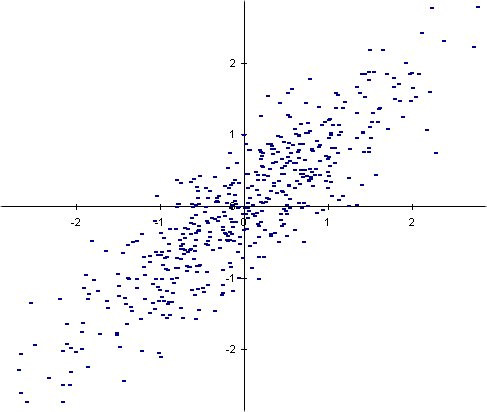
El gràfic d'una sèrie doble és un diagrama de dispersió (núvol de punts), i es forma representant en un sistema de coordenades els valors que prenen les variables x i y per a cada individu.
Quan els punts d'un núvol estan disposats
en forma aproximadament rectilínia direm que existeix correlació
lineal entre les dues variables. La correlació és positiva
o negativa segons ho sigui el pendent de la recta a què s'aproximen.
 |
 |
 |
|
|
|
|
La correlació positiva denota l'existència
entre les variables d'una relació que les porta a variar en un mateix
sentit: els individus en què x és alta són generalment
els individus en què y és alta, etc.
La correlació negativa denota l'existència
entre les variables d'una relació que les porta a variar en sentit
contrari: els individus en què x és alta són generalment
els individus en què y és baixa, etc.
És possible l'existència de correlacions altres que la lineal, si els punts d'un núvol es disposen seguint una corba d'un altre tipus.
Quan els punts d'un núvol estan molt dispersos diem que les variables són incorrelacionades.
L'existència d'una correlació entre dues variables no indica que hi hagi entre elles cap relació causal.
El grau de correlació lineal es mesura amb
el coeficient de correlació r . Es un nombre entre -1 i 1,
essent:
r = 1 : correlació positiva perfecta
r = -1 : correlació negativa perfecta
r = 0 : variables incorrelacionades
Es considera que hi ha una relació significativa
quan la correlació és més gran que 0,7.
Veure: Excel: Estadística bivariant
Veure: Exemples de núvols de punts