1.10 Exemples de variables aleatòries
A) Variable uniforme
Una experiència segueix el model uniforme si tots els resultats tenen la mateixa probabilitat.
Corresponen a la variable uniforme tots els jocs d'atzar equitatius.
B) Variable binomial
Un experiment aleatori s'anomena experiment de Bernoulli si només té dos resultats possibles. Diem 0 (èxit) i 1 (fracàs) als dos valors i p i q a les seves probabilitats: p+q=1.
Si es fan n proves d'un experiment de Bernoulli i X és la variable “nombre d’éxits” direm que X és una variable binomial B(n,p)
La probabilitat de cada valor de X és
.
Té mitjana E(X) = np i desviació tipus 
.
 |
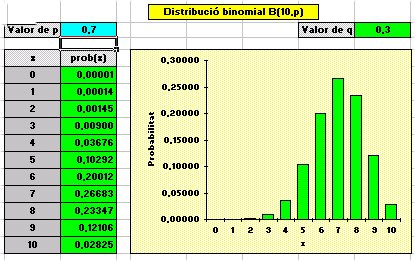Taula i gràfic de la distribució binomial B(10, 0,7) |
C) Variable de Poisson
Un experiment aleatori s'anomena experiment de Poisson si consisteix en observar l'aparició independent de successos en el temps. El nombre de successos observats en un determinat interval de temps és una variable aleatòria discreta que és la variable de Poisson.
La seva densitat és 
,
on k és un paràmetre propi de la situació. Té
mitjana E(X) = k, desviació tipus 
.
Es pot pensar que una variable estadística
segueix la distribució de Poisson quan té un perfil en forma
de L i la mitjana molt semblant a la variància.
 |
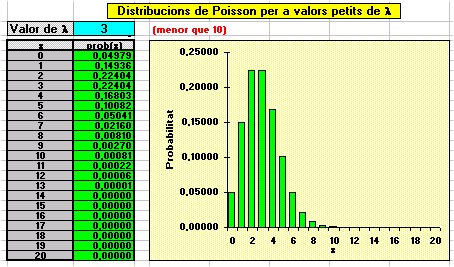Taula i gràfic de la distribució de Poisson de paràmetre 3 |
D) Variable normal
És una variable contínua que té
densitat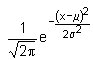 
.
S'anomena la normal N(µ ; 
).
La seva mitjana és µ i la seva desviació tipus és .
Per a una distribució N(µ ; )
l'interval [µ - ,
µ + ]
conté el 68,3% de les dades, l'interval [µ - 2,
µ + 2] el
95,4% i l'interval [µ - 3,
µ + 3] el
99,7%.
Hi ha molts processos reals de mesura i observació
que segueixen un model normal: en principi això té lloc si
els resultats de l'experiment depenen de moltes causes independents, cadascuna
de poca importància considerada aïlladament.
 |
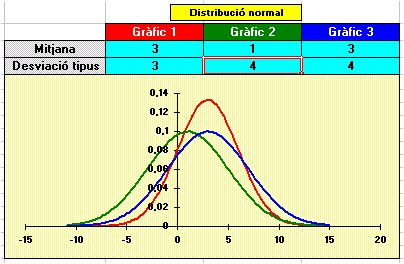Gràfics de les tres distribucions normals N(3,3) (en vermell), N(1,4) (en verd) i N(3,4) (en blau) |
Malgrat ser pròpia de les variables contínues,
també es pot aplicar la distribució normal a variables discretes.
En aquest cas per obtenir P(a 
X b) i si la separació
entre valors successius de la variable discreta és 1, es calcula
P(a-0,5 X
b+0,5). Aquesta adaptació s'anomena la
correcció de continuïtat.
Veure: Excel: Distribucions
Veure: Un exemple
