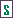Material per a l'alumnat	[Crèdit 5]
12

 

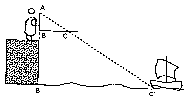
Tales ja ho feia Conten que Tales de Milet (un savi grec de la biblioteca d'Alexandria) ja feia servir un instrument semblant per saber on estaven els vaixells per fer-los senyals. Va arribar a formular l'equivalència de les fraccions següents: AB/AB' = BC/B'C' = AC/AC' Explica per què una fórmula com aquesta permet calcular la distància als vaixells. Pots fer de grec i calcular en cada cas la distància al vaixell: AB BC AB' B'C' 30 cm 60 cm 25 m 50 m   70 cm       110 cm       45 cm     Recorda Sempre que dues rectes es tallen per paral·leles, els segments corresponents són proporcionals. Això s'anomena Teorema de Tales. Problemes Constata que en una situació com la del dibuix, on hi ha triangles semblants (amb els mateixos angles), els segments corresponents són proporcionals. 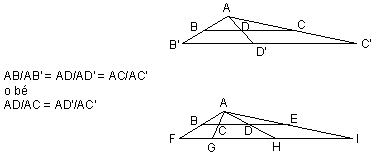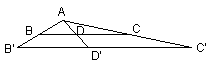Comprova que si AB/AB'=AD/AD' aleshores tambés és cert (AB'-AB)/(AB') = (AD'-AD)/(AD') Més coses Escriu totes les proporcions que es poden escriure a partir d'un dibuix com aquest. Justifica-ho.
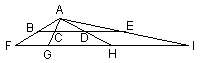