Material per a l'alumnat

 [Crèdit 6]
 
  
  
31  Sumant quadrats, utilitzem expressions
 		a b s p
 
Bon dia mates
 Recorda que
1+2+3+...+n = (1+n)·n/2

Analitza el procés següent i comprova que ens demostra que
1+4+32+...+n2 = n(n+1)(2n+1)/6

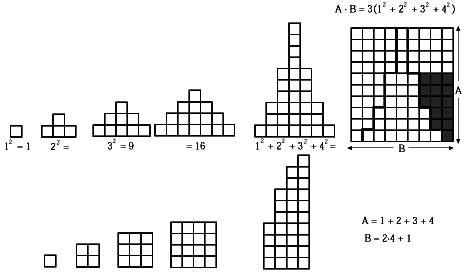
Procés

Suma dels
nombres quadrats		 Àrea del
rectangle		 Dimensió d'A Dimensió de B
12+22
12+22+32
12+22+32+42
12+22+32+42+52
12+22+32+42+52+62 		3(12+22+32+42) 1+2+3+4 2·4+1

Per a determinar-lo en el cas de n, observa que:

A·B = 3(12+22+32+42)

i tindrem que A = 1+2+3+...+n = n(n+1)/2
i B = 2·n+1
D'aquí surt el resultat volgut, fent simples operacions.