|
Del gràfic a l'optimització
Cal llegir la notícia i les seves condicions
| Un terratrèmol deixa la població de Cochabamba amb dificultats de supervivència. Unes 3.000 persones i 3.500 tones de material han de salvar-se el més ràpidament possible de la desfeta. El cost de l'evacuació és monumental. El cost d'un viatge des del lloc d'evacuació a la capital és de 50 milions amb un "Hèrcules" que transporta 60 persones i 10 tones de material, o bé seria de 40 milions amb un DC8 que portaria 30 persones i 14 tones de material. Davant les despeses, el govern decideix deixar 2.800 tones als serveis d'ajut d'altres països. Sabem que es compta amb 57 Hèrcules i 42 DC8, i cal ajustar les despeses. |
10x = càrrega Hèrcules (tm)
14y = càrrega DC8 (tm)
Si x = nombre d'Hèrcules (A)
y = nombre de DC8 (B)
60x = nombre de persones Hèrcules
30y = nombre de persones DC8
Condició pes: 14y+10x£700
Condició persones: 60x+30y£3000
Què podria representar 50x+40y < 240?
Com es "veuen" les condicions en un diagrama cartesià?
Si ens diuen que l'avió A porta 40 persones i 300 tones i l'avió B porta 30 persones i 200 tones,
- Què pot significar en nombre de persones x=30? I y<80 què pot significar pel que fa a material?
- Dibuixa les condicions corresponents a salvar 4.000 persones i 5.000 tones de material i justifica la frase: "les solucions estan dins un polígon de condicions".
Com obtenir, doncs, entre les línies paral·leles, la línia de cost òptim que compleixi condicions donades per un polígon?
Recorda
Un conjunt de condicions es tradueix algèbricament en un sistema d'equacions amb diverses lletres o gràficament en línies rectes. Els possibles resultats d'un problema de dues variables i diverses condicions acostuma a ser un polígon limitat per rectes que indiquen les condicions. L'optimització lineal de cost consisteix a trobar els punts de la funció cost que toquin el mínim el polígon de condicions en el sentit més favorable.
|
 Problemes
Problemes
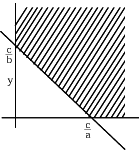
Una agència de comerç tracta dues mercaderies A i B. Per cada unitat de A obté un guany a i per cada una de B un guany b. Les despeses fixes són c. Justifica que el diagrama de la dreta explica els valors que aporten beneficis a l'agència.
Més coses
Inventa o busca un problema de condicions i procura resoldre'l.
|