|
- Per cada situació a), b) i c) anterior calcula les raons: altura de la visual/distància al punt 0. I sobre els corresponents esquemes mesura amb un transportador les inclinacions en graus de les visuals. Completa la taula següent:
| |
Angle de la visual |
Tangent de l'angle:
altures de la visual/distància al punt d'observació |
| a |
|
|
| b |
|
|
| c |
|
|
- Utilitza una calculadora científica, prem la tecla tan i completa les dades anteriors.
- Completa la següent taula amb la calculadora cinetífica:
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Angle |
0º |
1º |
2º |
3º |
4º |
5º |
10º |
15º |
25º |
30º |
|
|
|
|
|
|
|
| tangent |
|
|
|
|
|
|
|
|
|
|
0,25 |
0,5 |
0,75 |
1 |
1,2 |
1,5 |
1,7 |
- Expressa, mitjançant una fórmula que relacioni l'altura d'una muntanya, la distància al punt d'observació de l'angle
a de la inclinació de la visual.
Recorda
La raó a/b entre l'altura i la distància s'anomena tangent de l'angle d'inclinació a

|
Problemes
- Dibuixa un triangle rectangle ABC amb B=90º i la tangent de A igual a 3/5. Quina longitud té BC si AB mesura 10 cm? Utilitzant la taula anterior, determina aproximadament el valor de l'angle A.
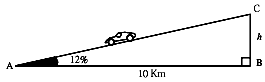
- Calcula l'altura de la carretera en el punt C. Pendent del 12%.
- Un planejador té una raó d'aterratge de 1:40. Està volant a 230 m sobre una ciutat i l'aeroport és a 9 km. Podrà aterrar?
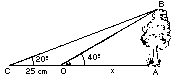
- Observant aquest esquema, descriu com determina l'altura de l'arbre. Calcula'ls utilitzant la taula o fent servir una calculadora.
Més coses
Fes un inventari de diferents instruments de mesura indirecta d'altures. Per cada instrument justifica la tècnica en què es basa.
Llegeix en el manual d'una calculadora científica l'ús de les funcions sin, cos, tan. Fes-ne un resum.
|