
|
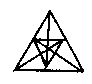
- Quantes triangles equilàters pots identificar? Agrupa'ls segons la mida.
- En un dau amb cares blanques, quins números posaries a les cares perquè sempre sortís un nombre senar?
- Un canal té una secció transversal en forma de trapezi de 8 m de profunditat, 14 m al llarg de la base i amb les parets formant un angle de 45º. Quina serà l'amplada superior del canal?
- Com s'ha de col·locar 10 espectadors per veure l'escenari d'un teatre amb un angle de 90º? Raona la teva resposta.
- Escull el resultat corresponent amb la calculadora
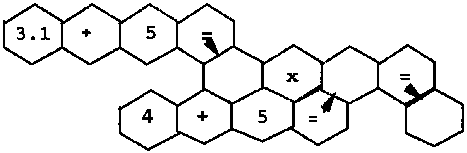
a) (5 + 4) x 3,1
b) 3,1 x (5 + 4)
c) (4 + 3,1) x 5
d) (4 + 3,1) x (4 + 5)
e) 4 + 3,1 + 4,5
- Omple les caselles amb nombres enters de manera que els totals per files i columnes sempre siguin 0.
- Raona si són correctes o no les desigualtats següents:
- 2x3x5 < 3x3x5
- 3x2x5x7 > 2x10x7
- "Si 1.000 = 2x5x2x5x2x5, aleshores 2x3x5x2x5x5 > 1.000".
- En una ciutat la temperatura augmenta a raó d'un grau per hora des de les 10 fins a les 19 hores; a partir d'aquesta hora disminueix a raó de 2 graus fins a les hores del dia següent. Fes una gràfica i una taula per representar aquestes variacions.
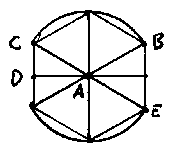
- Dibuixa amb regle i compàs aquesta figura. Expressa de la manera més precisa possible un itinerari que passi pels punts A, B, C, D i E.
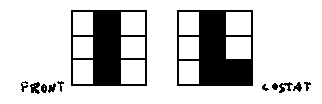
- Quants edificis podem construir que tingui les vistes següents?
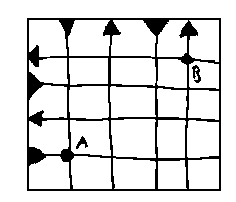
- Aquesta cuadrícula representa carrers amb els corresponents sentits de circulació. Descriu de la manera més acurada possible els camins possibles per anar en cotxe d'A a B. Raona quins són els més curts i els més llargs.
- Desxifra la paraula següent:
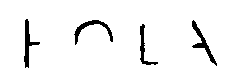
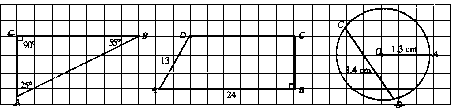
- Mira aquestes figures, algunes de les quals no estan dibuixades a escala, i investiga els errors possibles. Redacta breument els teus descobriments i dóna les explicacions corresponents.
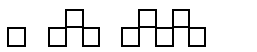
- Continua aquesta sèrie i expressa el procés de construcció general:
|