Imaginem
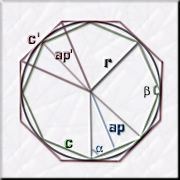
d'entrada, i per a començar, un triangle equilàter inscrit
en un cercle de radi, per exemple, igual a 1.
Imaginem
d'entrada, i per a començar, un triangle equilàter inscrit
en un cercle de radi, per exemple, igual a 1.
Ara es podrien plantejar una sèrie de qüestions:
- Quant mesuren els costats i els angles del triangle?
- Quina àrea ocupa aquest triangle?
- Quina àrea queda entre el cercle i el triangle?
Imaginem un quadrat o d'altres polígons:
- Podem trobar una norma per a resoldre aquests problemes?
De fet us recomano, si us motiva aquest tema, que tracteu de trobar algunes de les respostes a les qüestions proposades abans de seguir endavant.
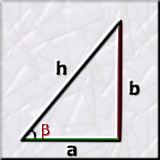 -
Les funcions trigonomètriques bàsiques, sempre aplicades
als triangles rectangles, són:
-
Les funcions trigonomètriques bàsiques, sempre aplicades
als triangles rectangles, són:
 La longitud de la circumferència, com ja sabeu, és
L =
2 · p·
r
La longitud de la circumferència, com ja sabeu, és
L =
2 · p·
r