Els comencem a conèixer des de ben joves, un bon dia arriba algun amic o conegut amb ganes de fer-nos rumiar una mica o de deixar-nos en evidència i ens proposa resoldre, al temps que dibuixa un quadrat dividit en tres parts horitzontals i verticals, el següent:
     ”A veure si ets capaç de situar els nombres de l’1 al 9 en aquesta graella de 3 per 3 caselles de manera que totes les files, columnes i diagonals sumin 15”
com si això fos la última novetat en passatemps... (Pobre infeliç!!)
    I tu que potser desconeixies el “problemeta” vas i t’escarrasses el cap una bona estona fins a adonar-te que el número 5 ha d’anar al centre del quadrat i llavors, sense masses dificultats, s’arriba a una de les moltes solucions possibles. Suposo que la majoria de nosaltres hem acabat sortint airosos d’aquesta experiència, que més o menys va ocórrer d’aquesta manera...
    En el meu cas recordo que quan vaig veure la seva solució i em vaig assabentar que els hi deien “quadrats màgics”, em va provocar, des del primer moment, una gran curiositat. Així que no en vaig tenir prou i vaig buscar, dedicant unes bones hores, de resoldre el “quadrat màgic de 4 per 4”.
    Des de llavors he sentit una gran fascinació per aquest tema, però no ha estat fins a recentment que he fet una investigació més seriosa dels “quadrats màgics”, fruit de la qual és aquest article que he dividit en quatre seccions:
        1. Història i curiositats dels quadrats màgics.
        2. Característiques dels quadrats màgics i algoritmes de càlcul.
        3. Estratègies de resolució dels quadrats màgics, d’ordre senar o parell.
        4. Galeria de quadrats màgics.

1. HISTÒRIA i CURIOSITATS DELS QUADRATS MÀGICS

    Sembla que els xinesos foren els primers en descobrir les curioses propietats dels quadrats màgics, que ells anomenaven “Lo Shu”, i, probablement, foren també els seus inventors al menys uns cinc segles abans de la nostre era.
    Una llegenda explica que el primer Lo Shu fou revelat als homes dibuixada a la closca d’una extranya tortuga que va emergir del riu Lo, d’aquí el seu nom ja que Shu vol dir “riu”.
    En el I Ching, el clàssic llibre xinès de les Mutacions i endevinació, apareix aquesta imatge del Lo Shu:

                (imatge del Lo Shu)                                                       (Lo Shu en xifres modernes)

     Els xinesos, per tant, els hi van atribuir un caràcter místic i creien que era un símbol que reunia els principis bàsics que formaren l’Univers.
     · Els nombres parells simbolitzaven el principi femení o Yin.
     · Els nombres senars simbolitzaven el principi masculí o Yang.
     · El número 5 representa la Terra, al seu voltant estan distribuïts els quatre elements principals, l’aigua 1 i 6, el foc 2 i 7, la fusta 3 i 8, els metalls 4 i 9.
     A més van construir quadrats màgics de més grandària, n’hi documentats alguns d’ordre 6, és a dir, que tenen un engraellat de 6 per 6.

     A Khajuraho (Índia) un temple construït entre els segles XI i XII té un pilar rodejat per una quadrícula amb un quadrat màgic d’ordre 4 el qual seria equivalent –traduint els caràcters- a la següent imatge:
 

     Com es pot observar fàcilment, totes les seves files, columnes i diagonals sumen 34. Però a més, les seves diagonals “trencades” (les línies imaginaries traçades des de cada número de la primera fila), les seves cantonades, els seus quatre quadrants i el quadrat central també sumen 34. Sens dubte, un treball impressionant d’algun matemàtic hindú!
    Els matemàtics àrabs van descobrir els quadrats màgics per contacte amb aquesta tradició hindú i també es van fascinar per les seves característiques i, probablement els van difondre per Occident durant l’Edat Mitjana.
L’engraellat d’aquest quadrat màgic àrab està format per les lletres de la paraula Alà. Totes les seves files, columnes i diagonals sumen 66, xifra que en el Islam correspon al valor numèric d’Alà.

( imatge del quadrat màgic d’Alà)

    El matemàtic Cornelio Agrippa (1486-1555) va construir quadrats màgics d’ordres 3 al 9 i els hi va atribuir un significat astronòmic, segons ell, representaven simbòlicament els planetes Mercuri, Venus, Mart, Júpiter, Saturn més el Sol i la Lluna, respectivament.
    Durant l’Edat Mitjana els quadrats màgics es gravaven en làmines de plata com amulets contra la pesta negra.
    El gran artista Albert Dürer fou també un distingit matemàtic que va publicar el 1.525 un tractat sobre la perspectiva, la geometria en tres dimensions i les seccions còniques titulat “Introducció a la mesura amb compàs i regla”, en el qual es descriu una cicloide per primera vegada.
    A més va incloure a la seva obra “Melencolia-1” un dels quadrats màgics més coneguts i que més han fascinat als estudiosos d’arreu.

    La gran varietat de detalls que apareixen en aquest gravat fan pensar que representa la insuficiència del coneixement humà per abastar la saviesa o per aprofundir en els secrets de la Natura. En  aquest gravat apareix també un sòlid insòlit, probablement, de la seva invenció.
    La característica més visible d’aquest superquadrat màgic és que l’any en que fou gravat, el 1.514, apareix a la seva part inferior. Totes les seves files, columnes i diagonals; les seves cantona-des, el quadrat central, els seus quatre quadrants, i les seves diagonals “trencades” sumen 34.
    Alguns matemàtics han volgut veure més propietats en el seu interior com, per exemple:

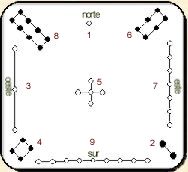
    · Si unim amb línies els nombres parells per una banda i els senars per l’altre, es formen estructures hexagonals!!

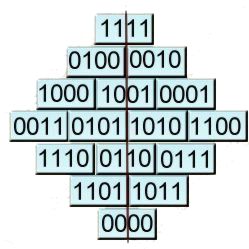
    · Si es tradueixen les seves xifres –restant-les una unitat a cadascuna, és a dir, quedarien les xifres del sistema hexadecimal (del 0 al 15)- a nombres binaris i girem el quadrat màgic 45º a la dreta apareix una simetria vertical perfecta de zeros i uns, com si aquests es reflectissin en un mirall!!
 

                                                   (imatge del quadre màgic binari) >>
 

    N’hi ha que pensen que el quadrat màgic de Dürer és un “arquetip ple de significat i misticisme”.
    Els astròlegs els aconsellaven com amulets protectors, precisament, contra la malenconia!

2. CARACTERÍSTIQUES DELS QUADRATS MÀGICS i ALGORITMES DE CÀLCUL

      Els quadrats màgics són estructures numèriques situades en una graella de n files per n columnes, per la qual cosa, n es denomina ordre del quadrat, així, per exemple, el Lo Shu és un quadrat màgic d’ordre 3; el del temple de Khajuraho i el de Dürer són d’ordre 4.

    Un quadrat màgic es diu que és “pandiagonal” quan totes les seves diagonals –les dues principals i les “trencades” en tots dos sentits-  sumen la xifra buscada o proposada.
    Pels musulmans, durant l’Edat Mitjana, els quadrats màgics “pandiagonals” d’ordre 5 amb la xifra 1 situada en el centre tenien una significació mística especial, donat que el número 1 és el símbol d’Alà, Ser Suprem i Únic.
 

    Observem, a més, que les quatre cantonades i el centre d’aquest quadrat també sumen 65.
    Un quadrat màgic es denomina “associatiu” quan les parelles de nombres oposades al centre sumen n² + 1. Aquesta és una característica més pròpia dels quadrats d’ordre senar.
    El Lo Shu, presentat anteriorment, és "associatiu" perquè, sumant les parelles oposades al centre, observem:

     “Lo Shu”:  Ordre 3;  nombres de l’1 al 9;  S(x) =  (33  + 3) / 2 = (27 + 3) / 2 = 15
     “Dürer”:    Ordre 4;  nombres de l’1 al 16;  S(x) =  (43  + 4) / 2 = (64 + 4) / 2 = 34

    Tractaré, ara, de generalitzar aquest algoritme per a qualsevol sèrie aritmètica de nombres.
    Si utilitzem una sèrie de nombres que siguin múltiples de l’l al n², o bé multipliquem tota la sèrie numèrica per la mateixa xifra, seguirem tenint un quadrat màgic, però el resultat obtingut serà també múltiple del resultat inicial.
    Així, si en el Lo Shu utilitzem les xifres parells consecutives començant pel 2, el resultat obtingut a cada línia serà 30, per ex. 2 + 10 + 18 = 30, (en lloc de 1 + 5 + 9 = 15), etc.
    Si en el “Dürer” utilitzem els múltiples de 5, el resultat obtingut serà 170:

    També podem començar la sèrie des d’un número a_i en lloc d’iniciar-la des de l’1, és a dir, si sumem (o restem) una determinada xifra t a tots els nombres de la sèrie 1 a n² el resultat augmentarà en n vegades la xifra sumada.
    Veiem-ne un parell d’exemples:
    Si sumem 10 a cada dígit del Lo Shu, llavors la sèrie comença a a₁ = 11 i acaba a a_x = 19, el resultat a obtenir és: 14 + 19 + 12 = 45 (en lloc de 4 + 9 + 2 = 15)
    Hem sumat 10 a cada una de les tres xifres i, per tant, el resultat augmenta 30 unitats.
    Si sumem 4 a cada dígit del Dürer, la sèrie comença a a₁ = 5 i acaba a a_x = 20, el resultat obtingut és:

    Generalitzant tots aquests casos, trobem que l’algoritme de càlcul ve donat per l’expressió:

    En la qual, n és l’ordre del quadrat, k és la constant del producte i t és la constant de l’addició.
    Aquest algoritme ens pot resultar de gran utilitat si volem definir o construir un quadrat màgic
de qualsevol mida i utilitzant sèries de nombres diverses.

    · Qüestió: Tenint en compte tot això, podríeu calcular per a un quadrat màgic d’ordre n:

3. ESTRATÈGIES PER LA RESOLUCIÓ DELS QUADRATS MÀGICS

    En aquest capítol us explicaré com resoldre correctament quadrats màgics de qualsevol ordre utilitzant estratègies o tècniques força senzilles, i probablement innovadores (cas de l’ordre parell), que són el fruit d’una recent investigació meva.
    El meu objectiu era establir un sistema manual, és a dir, sense l’ajut de l’ordinador, de normes per a resoldre o crear quadrats màgics de qualsevol mida amb les següents condicions d’ús: rapidesa, senzillesa, mecanització, seguretat i correcció. Aquests mètodes són el que presentaré a continuació.
    És cert que existeixen moltes altres solucions alternatives i de més dificultat o bellesa a les que trobarem aplicant aquestes tècniques, però es pot considerar que, aquest, és un “sistema bàsic”.
    Hem de distingir, a l’hora de l’estratègia a emprar per a la seva construcció, entre els quadrats màgics d’ordre parell i els d’ordre senar.
    Començarem per aquests últims donat que la dificultat per resoldre’ls és menor.
    El mètode bàsic consisteix en afegir lateralment als quatre costats sèries virtuals de caselles, de forma triangular, de manera que ens quedi la figura d’un rombe. (Pas número 1)
    Llavors, i començant des de l’extrem superior, situem totes les xifres –a partir de l’1- seguint només les diagonals alternes formades en el rombe, observeu que queden, per tant, línies diagonals i caselles interiors del quadrat en blanc. (Pas número 2)
    El quadrat màgic es completa situant els nombres que han quedat a les caselles “virtuals” exteriors del quadrat, a les caselles interiors en blanc, seguint primer una simetria horitzontal, les del triangle superior passen a completar la part inferior, com si el retalléssim i enganxéssim sense girar-lo i les del triangle inferior a la part superior; i una simetria vertical, les de la part exterior dreta a l’interior esquerra i a l’inrevés. (Pas número 3)
    Aquesta imatge il·lustra clarament aquest procediment:

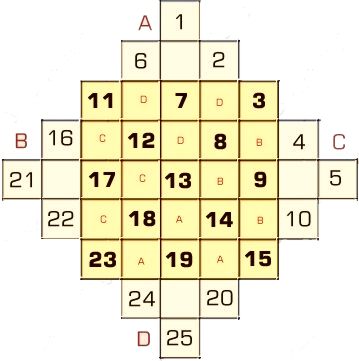
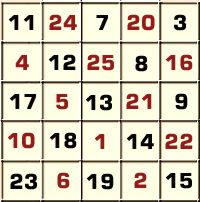
            És increïblement senzill!!
 

     Per a resoldre quadrat màgics d'ordre parell seguirem els següents passos, que són molt més fàcils d'aplicar del que pot semblar en un primer moment:
    Utilitzaré, en primer lloc, un quadrat d'ordre 4, que és el més petit dels d'ordre parell, per a aclarir-ho millor.
    · 1. Començarem per escriure el número 1 (o la 1ª xifra de la sèrie) a l'extrem superior esquerra i llavors escriurem, anant d’esquerra a dreta, només les xifres corresponents a les caselles que formen les dues diagonals principals.

    · 2. Ara ens situarem a la primera casella inferior dreta en blanc, veïna de la del extrem, on posarem el número 2 (o la 2ª xifra de la sèrie) i anirem desplaçant-nos cap a dalt en sentit de dreta a esquerra per anar completar, en estricte ordre, les caselles que faltes, és a dir, les que formen els interiors de les diagonals principals i les dues caselles exteriors de les files centrals.
    És a dir, posem el 2 i anem comptant d’un en un fins a arribar a una de les caselles esmentades, llavors escrivim aquesta xifra i seguim comptant, si s’acaba una fila pugem a l’anterior i canviem de sentit (ziga-zaga), fins a arribar a l’extrem superior esquerra.
    De fet, com es pot observar, el quadrat màgic d'ordre 4 ja ha quedat completament resolt.
 

    Extrapolaré, tot seguit, aquest mètode a quadrats màgics més grans d'ordre parell.
    Passarem, doncs, al quadrat d'ordre 6 i aplicarem els dos passos descrits anteriorment:
 

    · 3b. Finalment ens situarem a l'extrem inferior dret i amb un desplaçament de dreta a esquerra, anirem comptant d’un en un i escriurem només els nombres senars a les caselles corresponents que han de coincidir exactament amb les caselles que encara quedaven en blanc.
    (Els passos 3a i 3b poden invertir-se d’ordre sense afectar el resultat final)

   Un cop completat aquest quadrat màgic d'ordre 6 es poden extreure algunes conclusions, donat que aquest mètode és recurrent i només varien alguns detalls depenent de l'ordre del quadrat.
Hi ha tres factors determinants o que defineixen cada pas:
· El primer és indicar l’extrem d’inici: Superior (S) / Inferior (I), Dreta (D) / Esquerra (E)
· El segon el tipus de desplaçament a seguir: d’esquerra a dreta (E-D), de dreta a esquerra (D-E) o ziga-zaga (Z-Z)
· El tercer és l’acció a aplicar: completar diagonals (DG), interior diagonals(DGI), exterior diagonals centre (DGE), escriure parells (EP), escriure senars (ES), completar nombres restants (NR)
Definides les normes d’aplicació i la nomenclatura abreviada a utilitzar, acabaré aquest capítol amb unes taules de treball abreujades per a completar quadrats màgics d’ordre parell (4 al 12).
 

    Existeixen solucions alternatives o simètriques, però aquest mètode és bàsic, correcte i bastant senzill.

4. GALERIA DE QUADRATS MÀGICS

       Per acabar amb aquesta exposició, presentaré una modesta col·lecció de quadrats màgics, a afegir amb els anteriors, que em semblen molt interessants, curiosos o, fins i tot, petites obres d’art. D’exemples n’hi ha milers, i més actualment ja que amb els ordinadors es troben meravelles, però he donat preferència als composats manualment, digueu-me romàntic, o que aporten una idea original o estèticament brillant.
    Alguns són de collita pròpia, altres els he trobat durant la meva investigació...

    Aquest quadrat màgic d'ordre 10 (Déu), està format pels 100 primers nombres parells.
    Té la propietat de que la suma de les seves files, columnes i diagonals és igual a 1010 (Déu-Déu).
    Per cert, el nombre 1010 en sistema binari és igual al 10 en sistema decimal!!     1010₂ = 10₁₀

    Aquest quadrat màgic està compost exclusivament pels múltiples de 6 en un engrellat de 6 x 6 >> (666)
    Té la característica principal de que la suma de les seves files, columnes i diagonals és igual a 666.

    Aquest quadrat màgic d'ordre 12, està format pels 144 primers nombres senars, des de l'1 fins al 287.
    Té la propietat de que la suma de les seves files, columnes i diagonals és igual a 1728 = 12³.

    Aquest quadrat màgic d'ordre 8, està format pels nombres de l'1 al 64.
    Té la propietat de que la suma de les seves files, columnes i diagonals és igual a 260, però també ho és la suma de les seves quatre cantonades amb els quatre nombres centrals. La suma total de les caselles blanques i negres és idèntica, les forces es mantenen equilibrades, i igual a 1040.

    Aquest meravellós quadrat màgic d'ordre 4, té la sorprenent característica de ser pandigital, és a dir, que cada element està format per les deu xifres decimals sense repetir-ne cap i a més la suma de les seves files, columnes i diagonals és també pandigital S(x) = 4129607358.
    Probablement és la matriu pandigital d’ordre 4 més petita possible, donat que se’n poden construir d’altres amb nombres més grans.

    Aquest fantàstic quadrat màgic d'ordre 6 està compost exclusivament per nombres primers.
    La suma de les seves files, columnes i totes les seves diagonals, és a dir és pandiagonal, és igual a 666.

    Hi ha quadrats màgics que poden tenir la notable propietat de contenir un altre quadrat màgic al seu interior d'ordre inferior, per tant, són quadrats màgics dobles. Fins i tot se’n poden construir alguns que contenen successius quadrats màgics al seu interior en capes concèntriques.
    Aquí us proposo un exemple de quadrat màgic doble d'ordre 5 que conté en el seu interior un altre d’ordre 3.
    La suma de les files, columnes i diagonals del quadrat màgic d’ordre 5 és igual a 75, mentre que les del quadrat menor d’ordre 3 és igual a 45.
 

    Aquests dos quadrats màgics d'ordre 4 són especulars l'un respecte l'altre, una qualitat força rara i remarcable. La suma de les seves files, columnes i diagonals és en tots dos quadrats de 242, a més tots dos són pandiagonals.