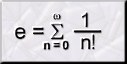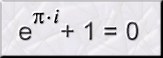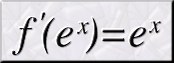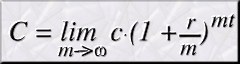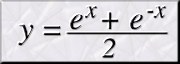De los
polígonos al círculo
Siempre me ha fascinado la imagen de un polígono regular inscrito en un
círculo que va aumentando su número de lados y se va acercando progresivamente a la figura del
círculo hasta, prácticamente, convertirse o
confundirse con él.
Por
ello quería hacer un pequeño estudio de este proceso, analizándolo de un modo gradual,
hasta llegar a diversas conclusiones de como se produce, de los cambios que
tienen lugar y obtener,
finalmente, una serie de resultados que simplifiquen el cálculo de las cuestiones implícitas en él.
 Imaginemos
de entrada, y para comenzar, un triángulo equilátero inscrito en un círculo de radio, por ejemplo, igual a 1.
Imaginemos
de entrada, y para comenzar, un triángulo equilátero inscrito en un círculo de radio, por ejemplo, igual a 1.
Ahora se podrían plantear una serie de
cuestiones:
- ¿Cuánto miden los lados y los ángulos del triángulo?
- ¿Qué área ocupa este triángulo?
- ¿Qué área queda entre el círculo y el triángulo?
Imaginemos un cuadrado u otros polígonos:
- ¿Podemos encontrar una norma para resolver estos problemas?
De hecho os recomiendo, si os motiva
este tema, que tratéis de hallar algunas
de las respuestas a las cuestiones propuestas antes de seguir adelante.
-
Dado que algunos de vosotros
podríais ser profanos en esta materia, de entrada, definiré algunos aspectos geométricos
de forma
breve.
-
-
(saltar conceptos básicos)
-
-
Conceptos básicos
-
-
Para calcular lo que miden los ángulos interiores de un polígono
regular se procede así:
· La suma total de los ángulos
de un polígono es igual
al número de lados menos 2 y multiplicado por 180º, es decir: Suma de
ángulos = (n - 2)· 180º (n
es el número de lados)
· En el caso de los polígonos regulares, podemos calcular lo que mide cada
ángulo interior dividiendo el resultado anterior entre el número de ángulos o
lados que tiene, es decir:
-
ángulo
= (n - 2)· 180º / n
-
Ej. Para un octágono regular (ocho lados) la suma de sus ángulos
interiores es:
-
(8
- 2)· 180º = 6 · 180º = 1080º
-
y cada uno de sus ángulos mide: 1080º
/ 8 = 135º
- El apotema de un polígono es el altura de cada uno de los triángulos en que
podemos descomponer un polígono y que tienen por vértice
el centro del polígono y los dos extremos de cada lado.
- El perímetro de un polígono es la suma total de lo que
miden sus lados.
En el caso de los polígonos regulares se puede aplicar la siguiente
fórmula:
-
pi = n · c (n =
número
de lados, c = longitud de los lados)
-
- El área de un polígono de más de 4 lados se calcula
efectuando el semiproducto de se perímetro pi por
el apotema ap:
A = pi · ap / 2
-
La longitud de una circunferencia es igual al doble del radi per
PI:
L = 2 · PI · r
-
El área de un círculo es igual al producte de PI por el radio al
cuadrado: A = PI · r2
-
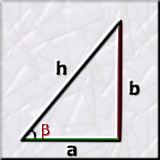 -
Les funciones trigonométricas básicas, siempre aplicadas a los triángulos rectángulos, son:
-
Les funciones trigonométricas básicas, siempre aplicadas a los triángulos rectángulos, son:
· El seno del ángulo, que es el cociente entre el cateto
b
opuesto al ángulo y la hipotenusa
h:
sin ß = b / h
· El coseno del ángulo, que
es el cociente entre el cateto a contiguo
al ángulo y la hipotenusa h:
cos ß = a / h
· La tangente del ángulo, que es el cociente entre el cateto
b
opuesto al ángulo y el cateto a contiguo, o
bien el cociente
entre el seno y el coseno del ángulo: tg ß
= b / a o bien tg ß
= sin ß / cos ß
-
Gracias
a las calculadoras científicas el cálculo de estas funciones es muy sencillo
y su aplicación en la resolución de problemes geométricos puede simplificar
mucho la cuestión.
-
-
-
¥
-
NÚMEROS TRASCENDENTES
-
-
Historia del número
p
-
-
El número pi ha fascinado a lo largo de
los tiempo a numerosos matemáticos, científicos
o simples aficionados al cálculo, hasta el punto de que algunos li dedicaron gran parte de
sus vidas en hallarlo, calcularlo, etc.
El número pi no es un número entero ni se puede
expresar como el resultado de una
fracción, sino que no tiene límite, es decir, tiene infinitos decimales
y, por tanto, nunca se podrá calcular completamente, pertenece al conjunto de
los números reales, pero dado
que no es la raíz cuadrada de ningún número, se dice que es un "número transcendente".
Parece
que fue W. Jones el primero que empleó la letra griega pi para designarlo en su libro "Introducción a
las matemáticas"
(1.706), por ser la inicial de la palabra periferia (circunferencia).
Los egipcios ya conocían que la relación entre el diámetro y la longitud
de una circunferencia no se podía calcular con exactitud y la expresaron com
3 + 1/6 ó 3,16.
Muchos
siglos después el gran Arquímedes de Siracusa diseñó
el método de los polígonos inscritos y circunscritos para calcularlo,
que comentaré más adelante.
Así
obtuvo el valor de pi =
3 + 1 / 7 ó 22 / 7 = 3,1428
Ptolomeo calculó que pi =
3 + 1 / 8 + 1 / 60 = 3,14166
Los matemáticos árabes y chinos habían hallado que
pi era
igual a 3,1416
Este
procedimiento estuvo vigente hasta el siglo XVII, a partir de aquí los matemáticos comenzaron a diseñar algoritmos de
cálculo, en los que
no interviene la circunferencia, cada vez más originales y eficientes y los progresos
fueron relativamente rápidos, yo destacaría algunos como:
p =
2
x 2 x 4 x 4 x 6 x 6 x ... Algoritmo de Wallis
2
3 x 3 x 5 x 5 x 7 x 7 x ...
p =
1 + 1
+ 1
+ ... Algoritmo de Leibniz
8
1 x 3 5 x 7 9 x 11
p2
=
1 + 1 + 1 + 1
+ ... + 1 , o sea,
p2
= 6 · S (1/n2) Algoritmo
de Euler
6 4 9 25
n2
Así
el número de decimales hallados de pi fue aumentando
sin parar:
Van Ceule
encontró 35 que hizo grabar en su tumba.
Sharp halló 72,
Lagny: 127, Vega: 139, Rutherford llegó a los 208
en 1.841 y a 440 en 1.872, pero el británico William
Shanks, que dedicó 20 años de su vida, estableció la última
gran marca de los calculistas, digamos manuales, al llegar al decimal 707 en
1.874. Fue homenajeado como un héroe y se escribieron bajo la cúpula
del palacio de la Découverte de Paris.
Desgraciadamente en el año 1.947, D. F. Ferguson descubrió que el decimal 528 era
incorrecto, y obviamente todos los siguientes...
A partir
de la década de los 40, la aparición de los ordenadores ha permitido profundizar, rápidamente, en el
cálculo de pi,
así en 1.949 se llegó a los 2.036 decimales, en 1.959 ya eran 10.000, en 1.974
se consiguieron obtener 1.000.000. Uno de los últimos
récords sobrepasaba los 6 mil millones en 1.995.
Aquí
tenéis, a título informativo, los 100 primeros decimales de
pi que,
obviamente, no aplicaréis en vuestros problemas geométricos,
pero que siempre son curiosos de ver e, incluso, os pueden
servir de entrenamiento memorístico. ¿Os atrevéis?
pi = 3,1415926535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164
0628620899 8628034825 3421170679 ...
-
-
Un sencillo algoritmo de
cálculo del número
p
-
Para
acabar este capítulo dedicado al número pi,
os propongo un algoritmo bastante sencillo para calcular de manera aproximada
una buena serie de decimales.
El procedimiento está basado en el método de los
polígonos inscritos y circunscritos de Arquímedes, pero claro, con la
ventaja actual
de las calculadoras científicas.
De esta
manera nos acercaremos al método de cálculo de pi
que estuvo vigente durante casi dos mil años y lo podremos comprender mejor.
Este procedimiento consiste en calcular los perímetros de los dos
polígonos regulares uno inscrito y el otro circunscrito y compararlos con la longitud
de la circunferencia, de esta manera podemos hallar dos valores diferentes
de p,
uno inferior pi
correspondiente al polígono inscrito y el otro superior
pc
obtenido con el circunscrito.
Entonces podremos concluir que p
es la media aritmética de ambos valores hallados:
-
p
= (pi
+ pc)
/ 2
-
 La longitud de la circunferencia, como ya sabéis, es
L =
2·p·r
La longitud de la circunferencia, como ya sabéis, es
L =
2·p·r
El perímetro de un polígono regular inscrito es:
p = n · c
c = 2 · r · cos a
(expresando la medida del lado
c en función del radio
r),
n es el número de lados del
polígono.
Para simplificar el cálculo se toma como radio el valor
r = 1
Sustituyendo se obtiene:
p =
2 · n · cos a
El ángulo
a es la mitad de los ángulos interiors
b
del polígono regular que podemos obtener con la fórmula vista
anteriormente:
-
b =
(n - 2) · 180º / n, a = b
/ 2
-
Si ahora igualamos la longitud
de la circunferencia con el perímetro
del polígono inscrito, obtenemos el valor
pi, es
decir, el límite o valor inferior de p para este
polígono:
-
2
· n · cos a =
2 · pi
=>
pi
= n
· cos a
-
El perímetro
del polígono regular circunscrito es: P' = n · c'
c'
= 2 · r / tg a (fijaos
que para el polígono circunscrito el apotema ap'
es igual al radio)
Por tanto: P' = 2 · n / tg a
Igualando la longitud de la circunferencia con el perímetro del
polígono
circunscrito, se obtiene el valor pc,
es decir, el límite o valor superior de p:
-
2
· n / tg a =
2 · pc
=> pc
= n
/ tg a
-
Finalmente obtenemos que p = (pi
+ pc)
/ 2
-
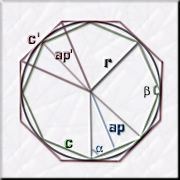
Veamos
unos ejemplos aclaratorios:
En el
caso del octágono de la figura, y con ayuda de la calculadora científica,
tenemos que:
n
= 8
b =
(8 - 2) · 180º / 8 = 135º, a = b
/ 2 = 67,5º
pi
= 8
· cos 67,5º = 3,061467458920718173827
pc=
8
/ tg 67,5º =
3,313708498984760390413
pi = (pi
+ pc)
/ 2 = 3,1875879789527392821205
Un
valor de p todavía
no muy correcto.
Pero si ahora probamos con un polígono regular de n = 10.000
lados, veremos que:
b =
(10.000 - 2) · 180º / 10.000= 179,964º, a = b / 2 = 89,982º
pi
= 10.000
· cos 89,982º = 3,14159260191266569297934647928899
pc=
10.000
/ tg 89,982º =
3,14159275694405291972467077191176
pi = (pi
+ pc)
/ 2 = 3,14159267942835930635200862560038
Un
valor que ya es correcto hasta el séptimo decimal y, por lo tanto, muy interesante...
Lógicamente se puede seguir buscando más precisión con sólo aumentar el número
de ángulos del polígono regular que tomemos como base del cálculo, pero esto, si
os ha gustado el tema, ¡ya es tarea de investigación vuestra!
-
-
-
El
número e:
Aplicaciones y curiosidades
-
-
-
Autora: Bharti Pridhnani
El número e
es un número real, dentro de estos es irracional y trascendente, lo cual
quiere decir que no es raíz de ningún polinomio con coeficientes
de números racionales.
Su valor es de 2,718281828459045...,
tiene infinitos decimales y estos no son periódicos.
El número e se define como
el límite cuando n tiende a infinito de la
sucesión (1+1/n)n, o sea:

Otra definición del número e
es el sumatorio desde 0 hasta infinito de 1/ n!. Se indica:
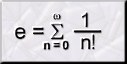
El número e
primero fue estudiado por el matemático Leonhard Euler (1720) aunque destaca más
por su trabajo John Napier, el inventor de los logaritmos
(1614).
Euler fue el primero en utilizar
la letra e en 1727 para esta constante, y también
calculó hasta 23 decimales en 1748 utilizando la fórmula del sumatorio.
Más tarde, W. Shanks llegó a los 205 decimales en 1871, número que fue superado
en 1884 por Boorman, que
calculó 346.
Con la llegada de las computadoras
el cálculo se simplificó y rápidamente los progresos fueron
enormes, así:
· J. von Neumann y su grupo utilizaron el ENIAC para obtener 2.010 decimales en 1949.
· D. Shanks y J.W. Wrench hallaron hasta
100.265 en 1961 con la fórmula de Euler con un IBM 7090. Se emplearon 2,5 horas.
· R. Nemiroff
y J. Bonnell ya llegaron a 10.000.000 decimales en 1994.
· Shigeru Kondo
y X. Gourdon obtuvieron 12.884.901.000 en agosto de 2000, usando el programa de
cálculo PiFast33 en
un Pentium III 800. Se necesitaron 167 horas.
Curiosidades sobre el número
e
· La fórmula d’Euler:
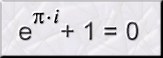
En esta fórmula se observan tres
tipos de números: e,
p y el número imaginario
i, es decir, aquí intervienen las constantes
matemáticas más importantes: 0, 1, e,
p, i
· La derivada de ex:
La derivada de ex es ella misma, es la única función real que
lo cumple, es decir:
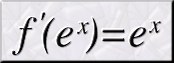
· Aproximación al número e
por medio de números racionales:
Podemos hacer una aproximación al número
e por medio de números racionales a pesar de que
éste sea irracional:
e = 2 +
1 _
1 +
1 _
2 +
1 _
1 +
1 _
1 +
1 _
4 +
1 _
1 +
1 _
1 + 1 _
6 + 1 _
1 + ...
Aplicaciones del número e
Veremos ahora varios ejemplos de aplicaciones
del número e en diversas ciencias, he escogido algunas que nos pueden
parecer más próximas
a nuestra vida cotidiana y que, quizás, os sorprenderán:
· Intervención del
número e
en un asesinato:
Una aplicación del número “e” es poder determinar en un asesinato el momento de la muerte.
Es necesario aplicar la ley de Newton sobre
el enfriamiento que establece que la velocidad a la que se enfría un cuerpo es proporcional a la diferencia entre la temperatura del objeto
y la temperatura del entorno.
Esto quiere decir que cuando un objeto está mucho más
caliente que el aire exterior, su velocidad de enfriamiento es alta, de manera
que se enfría muy rápidamente; cuando un cuerpo está un poco más caliente que su
entorno, su velocidad de enfriamiento es baja y se enfría lentamente.
Una persona viva no se enfría continuamente.
El metabolismo humano asegura el mantenimiento de la temperatura del
cuerpo alrededor de los 36ºC (98,6º F). Pero una persona muerta deja de
producir calor y, por tanto, comienza a enfriarse siguiendo la ley
de Newton que se aplica con la fórmula matemática siguiente:
T = Taire + (Tcos – T aire)
/ ek·t
Dónde T es la temperatura, t es el tiempo en horas
después de medianoche y k es una constante.
Ahora aplicaremos esta fórmula en el asesinato de una persona.
Su temperatura en un momento dado después
de su muerte era de 85º F y la temperatura del aire era de 68º F.
A las dos de la madrugada la temperatura del cuerpo había disminuido hasta los 74º F.
A partir de esto nos interesa determinar cuando murió esta
persona. Sabemos que la temperatura normal del cuerpo es de
98,6ºF, se puede calcular el momento de su muerte operando así:
98,6º = 68º + (85º - 68º)
/ e0,5207·t
Operando los términos resulta: (30,6º)
· e0,5207·t
= 17º
e0,5207·t
= 17º / 30,6º = 0,5556
Por tanto, si aplicamos el cálculo
de logaritmos resulta:
0,5207 · t = L(e0,5207·t)
= L(0,5556) = -0,5878
t = -0,5878 / 0,5207 = -1,13
horas = -68 minutos
Con esto sabemos, gracias
a la ayuda del número e, que esta persona murió 68
minutos antes de las doce de la noche, es decir, a las 22:52 h.
-
-
· En matemática financiera se utiliza
para calcular el interés continuo:
La fórmula del interés
continuo es: C = c ·
(1 + r / m)m·t
dónde C =
capital final, c = capital inicial,
r = interés anual, m =
periodos de capitalización,
t
= número de periodos.
Veremos la aplicación del número e en matemática financiera a partir de un
ejemplo concreto.
Veamos lo que producen 1000 euros
a un interés compuesto del 20% anual en un año, y a interés continuo.
a) Primer caso: Cuando el periodo
de capitalización es 1 año:
C = c · (1 +
r / 1 )1 = 1000 · (1 + 20/100)1 = 1000 ·
1,2 = 1200 euros
b) Segundo caso: Cuando el periodo
de capitalización es 1 mes, es decir, hay 12 periodos
de capitalización al año, entonces la fórmula es:
C = c · (1 +
r / 12 )12 = 1000 · (1 + 0,2 / 12)12 = 1219,39
euros
c) Tercer caso: Cuando el periodo
de capitalización es 1 dia, es decir, hay 365 periodos
de capitalización al año tenemos que:
C = c · (1 +
r / 365 )365 = 1000 · (1 + 0,2 / 365)365 =
1221,34
euros
Si nos fijamos vemos que cuantos más
periodos de capitalización haya al año, el capital final producido es mayor, pero
parece que tiende
a estabilizarse al aumentar el número de periodos porque,
por ejemplo, la diferencia entre el capital final del segundo y tercer
caso es menor que la del primer y segundo caso.
Cuando el número de periodos de capitalización m
tiende
a infinito, el interés se denomina continuo.
La fórmula de este tipo de interés es, por tanto:
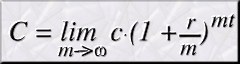
Ahora haremos una serie de transformaciones
con el fin de poder calcular este límite a partir del número e.
Si consideramos que r / m = 1 / (m
/ r) y ahora sustituimos m / r = n, y además
tenemos en cuenta que el límite de una constante por una función es igual a la constante por el
límite de la función, obtenemos:
C = c · lim
(1 + 1 / n)n·r·t
n->w
Que podemos transformar siguiendo las propiedades de los
límites en:
C = c ·[ lim
(1 + 1 / n)n]r·t
n->w
y como hemos visto, a la definición del número
e:

Por lo cual llegamos a la fórmula final
del interés continuo:
C = c
· er·t
Entonces, si los 1000 euros los tenemos
ahora a interés continuo, el capital final será:
C = c · er·t=
1000 · e0,2·1
=
1221,40
euros
El interés continuo es,
por tanto, el de máxima producción.
¿Habíais imaginado alguna vez que vuestros ahorros estaban
bajo el control del número e?
· En ingeniería:
Cuando se cuelga una cadena o un cable por los extremos,
tiende a adoptar una forma que se relaciona con el número e.
La fórmula es la siguiente:
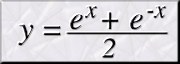
Así que, a partir de ahora, cada
vez que veáis un cable, una cuerda, etc. colgado por los extremos, pensad que
¡el número e está allí dándole la curvatura correspondiente!
· El carbono 14:
Para determinar de una manera aproximada
la antigüedad de un objeto que está formado por materia orgánica
se mide la cantidad de carbono 14 que contiene. Los seres
vivos tienen una cantidad de carbono 14 constante.
Cuando un ser vivo muere esta
cantidad se va desintegrando. La función que regula la desintegración se determina
con la siguiente fórmula:
Q = Qo · e-0,000124·t
Dónde Q es la
cantidad de carbono 14 final, Qo es la cantidad de carbono 14 inicial, t
es el tiempo.
· Espiral logarítmica:
En los seres vivos hay curvas relacionadas con el número
e. Una de ellas es la espiral logarítmica, la fórmula de
la cual es:
r = ea·j
· Absorción de los rayos X per la materia.
Ley de Bragg-Pierce:
I = Io · e-m·x
Dónde
I es
la intensidad final del rayo después de atravesar el cuerpo,
Io es la intensidad inicial de los rayos X,
m es el coeficiente de absorció,
x es el grueso del cuerpo.
· Crecimiento exponencial:
Una de las numerosas aplicaciones en biología del número
e es el crecimiento exponencial. Este tipo
de crecimiento surge cuando no hay factores que limiten el crecimiento.
Pueden experimentar un crecimiento exponencial las especies pioneras que llegan,
por ejemplo, a zonas despobladas como una superfície
boscosa en recuperación después de un incendio.
Para este tipo de crecimiento se aplica la
siguiente fórmula:
N = No · et
Esto nos permite adivinar cual será
la población N en un tiempo
t a partir de la población inicial
No.
· Crecimiento logístico:
Otro tipo de crecimiento es el logístico. Muchas
veces las circunstancias, como, por ejemplo, la
intervención del gobierno o las condiciones extremes de supervivencia,
limitan el crecimiento. Este tipo de crecimiento viene dado por la siguiente
fórmula:
f(x)
= k / (1 + a · e-b·x)
Dónde k,
a
y
b són constantes que se hallan experimentalmente, dependen de cada aplicación concreta.

-
Hay
muchas más aplicaciones de fenómenos o situaciones donde interviene
el número e, pero
me parece que después de leer este artículo -obtenido a partir del trabajo de
investigación de la alumna Bharti
Pridnani de Lloret- tendréis un concepto muy diferente de este maravilloso número
irracional y trascendente, pero poco conocido, que es el número
e.
-
-
(índice matemaravillas)

Volver al índice general
Autor: Blai Figueras Álvarez

E-mail:
mentaludix@hotmail.com
 Imaginemos
de entrada, y para comenzar, un triángulo equilátero inscrito en un círculo de radio, por ejemplo, igual a 1.
Imaginemos
de entrada, y para comenzar, un triángulo equilátero inscrito en un círculo de radio, por ejemplo, igual a 1.
 -
Les funciones trigonométricas básicas, siempre aplicadas a los triángulos rectángulos, son:
-
Les funciones trigonométricas básicas, siempre aplicadas a los triángulos rectángulos, son:
 La longitud de la circunferencia, como ya sabéis, es
L =
2·p·r
La longitud de la circunferencia, como ya sabéis, es
L =
2·p·r