En esta página quiero
comentar una serie de hallazgos numéricos -de mi cosecha- que podrían
considerarse 'curiosidades' matemáticas y que, en muchos casos, pueden ser
recursos muy interesantes para hacer cálculo mental rápido o para las clases de
esta materia.
¿No habéis probado nunca
de sorprender a otros con cálculos espectacularmente rápidos,
os puedo garantizar que en muchos casos sólo son pequeñas
estrategias bien entrenadas. Os presentaré varias...
Estoy
investigando toda clase de métodos de cálculo mental o rápido
y otros aspectos curiosos e iré ampliando esta sección progresivamente.
Los he agrupado en los siguientes
bloques:

-
 LOS FASCINANTES CUADRADOS MÁGICOS
LOS FASCINANTES CUADRADOS MÁGICOS
Historia y curiosidades
de los cuadrados mágicos.
Características
de los cuadrados mágicos y algoritmos de cálculo.
Estrategias para la resolución
de los cuadrados mágicos, de orden impar o par.
Galería de cuadrados mágicos.
-
-
 EL MARAVILLOSO TRIÁNGULO ARITMÉTICO
EL MARAVILLOSO TRIÁNGULO ARITMÉTICO
Introducción y
biografías de los matemáticos relacionados
Características
y propiedades del triángulo aritmético
¿Novedades en el triángulo aritmético?
- Números
triangulares y hexamórficos.
 NÚMEROS AL CUADRADO
NÚMEROS AL CUADRADO

Distancia
entre números al cuadrado
Un método rápido de calcular números al cuadrado
Método
de los "productos equidistantes"
 TRIÁNGULOS PITAGÓRICOS
TRIÁNGULOS PITAGÓRICOS
Expresiones matemáticas para obtener triángulos rectángulos con valores enteros
Cálculo de la diagonal de una figura geométrica
que no existe!
 MÚLTIPLOS y DIVISORES
MÚLTIPLOS y DIVISORES
Criterios
de divisibilidad
Múltiplos "sinceros"
Números "perfectos", "casi-perfectos" y números
"amigos"
-
-
 PRODUCTOS ALTERNATIVOS
PRODUCTOS ALTERNATIVOS
Contar
con los dedos está mal visto, multiplicar puede ser divertido!
Un
método diferente y más rápido de multiplicar
Un
método lineal de hacer productos en cruz
-
-

-
 DECIMALES PERIÓDICOS
DECIMALES PERIÓDICOS
La
sorprendente belleza de la infinidad
Periodicidad
de ciclo completo y de ciclo parcial
-
-
 RAÍCES SORPRENDENTES
RAÍCES SORPRENDENTES
- Un calculista muy rápido
y listo!
Origen del algoritmo
o método de cálculo de las raíces cuadradas
-
-

-
 CUADRADOS INTERCALADORES
CUADRADOS INTERCALADORES
Números que elevados
al cuadrado presentan una curiosa propiedad
-
-
 CASTELLERS NUMÉRICOS
CASTELLERS NUMÉRICOS
Ven
a la "Fiesta Castellera" de Númerolandia
-
-

 TRANSBASES
TRANSBASES
¡Si
las gallinas contasen!
La vida en Chip-landia-
-
-
 POTENCIAS
CURIOSAS
POTENCIAS
CURIOSAS
-
De
los días del año a Fermat

Sucesiones piramidales
y otras relaciones destacables
¡Un teorema mítico!
-
-
 GEOMETRIZANDO
GEOMETRIZANDO
De
los polígonos al círculo
-
-

-
 NÚMEROS
TRASCENDENTES
NÚMEROS
TRASCENDENTES
-
Historia del número
p
Un sencillo algoritmo
de cálculo del número
p
- El número
e:
Aplicaciones y curiosidades

 POESÍA AL NÚMERO
p
POESÍA AL NÚMERO
p
Haciendo honor
a la cita del gran Gustave Flaubert: "La poesía es una ciencia exacta como
la geometría" he compuesto un poema que ¡permite conocer o memorizar los 63
primeros decimales del número
p!
-
-
 SISTEMA MNEMOTÉCNICO PARA NÚMEROS
SISTEMA MNEMOTÉCNICO PARA NÚMEROS
-
Creéis que tenéis
mala memoria y no sois capaces de memorizar cadenas de números?

 PASATIEMPOS y ACTIVIDADES
PASATIEMPOS y ACTIVIDADES
Os
propongo una buen rato de distracción, pero ¡no tengáis miedo,
los hay fáciles!
 CHANZAS MATEMÁTICAS
CHANZAS MATEMÁTICAS
¡Las matemáticas también pueden hacernos
reír un rato!

 MATEJUEGOS
MATEJUEGOS
Una colección de
juegos matemáticos muy interesante para el aula o para gozarlos
Volver a
la página principal

NÚMEROS AL CUADRADO
Distancia entre números
al cuadrado
"La
distancia o diferencia entre 2 números consecutivos al cuadrado es la suma de
ambos".
Ejemplos:
8² = 64, mientras que 9² = 81. Su diferencia 81 - 64 = 17, es
decir, 9 + 8 = 17
Esto
es válido en todos los casos... 24² = 576,
25² = 625, la diferencia es 49 = 24 + 25
A partir de aquí podemos definir que la distancia entre 2 números
cualquiera al cuadrado es la conocida fórmula, tantas veces memorizada,
pero quizás no siempre valorada en este aspecto del cálculo:"La
distancia entre 2 números cualquiera al cuadrado es la suma por la diferencia".
a² - b²
= (a + b) · (a - b)
Ejemplo:
9² = 81, 5² = 25, 81 - 25 = 56, es decir: (9 + 5) · (
9 - 5 ) = 14 x 4 = 56
Esto, obviamente, nos puede permitir
calcular números al cuadrado a partir de los que ya conocemos:
Ej. Cuánto será 26²,
si sabemos que 25² = 625 ?
Sólo tenemos que sumar 25 +
26 = 51, y esto, añadirlo al 625, o sea, 625 + 51 = 676
Ejercicio: Cuánto es 37²,
si sabemos que 30² = 900 ? >>>
Suma = 67, Diferencia = 7
Con un poco de habilidad calcularemos
67 x 7 = 469 y lo sumaremos a 900, para obtener: 37² = 1.369
EJERCICIO: Cuánto
es 54², si sabemos que 50² = 2.500 ?
Cuál será la diferencia entre 41² y 26²
? (solución)

- Un
método rápido de calcular números al cuadrado
-
-
a) Comenzaré con el
cuadrado
de los números de 2 cifras acabados en 5:
El
cuadrado de los números
tipo 15, 25, 35, etc. se puede hacer de manera muy rápida:"Multiplicando
la decena propia por la siguiente y añadiendo un 25 detrás"
-
Veamos ahora algunos ejemplos:
Ej. 15²: multiplicamos su decena 1
por la siguiente 2, y obtenemos 2
añadimos un 25 detrás y tenemos el 225, que es 15².
Ej. 45² : 4
x 5 = 20, añadimos el 25 y sale 2.025 = 45²
Ej. 65² : 6
x 7 = 42, añadimos el 25 y ya esta el 65² = 4.225
(¿sorprendente o no?)
-
-
b) Cuadrado de los números de
dos cifras acabados en 1:
El
cuadrado de los números
tipo 11, 21, 31, etc. se puede calcular de modo rápido en tres partes:"Cuadrado
de la decena, el doble de la decena, añadimos un 1"
-
Ejemplos: 11²: cuadrado de la decena 1 x 1 = 1
el doble de la decena 1 + 1 = 2
le añadimos un 1 >>>> y obtenemos el 121 = 11²
Ej. 31²: cuadrado
de la decena 9, el doble de la decena 6, le añadimos un 1
>>> 31² = 961 Si la suma
de las decenas pasa de 9, entonces nos llevamos 1 al construir el número:
-
Ej. 61²: cuadrado de la decena 36, el doble de la
decena 12 en este caso, al pasar de 9 la suma
nos llevamos 1, o sea, 372, y le añadimos un 1 >> 61²
= 3.721
-
-
c) Cuadrado de los números de
dos cifras acabados en 9:
El cuadrado de los números
tipo 19, 29, 39, etc. se puede calcular de manera rápida en tres
partes: "Al cuadrado de la decena siguiente
le añadimos el 0, restamos el doble de la decena siguiente y añadimos
un 1"
-
Ej. 29²: cuadrado de la
decena siguiente 3 x 3 = 9, añadimos el 0, o sea, 90
le restamos el doble de la decena 3 + 3 = 6, es decir, 90 - 6 = 84
le añadimos un 1 >>>> y obtenemos el 841 = 29²
Ej. 49²:
cuadrado de la decena siguiente 25 >> 250, restamos el doble de la decena
siguiente 10, 250 - 10 = 240, le añadimos un 1 >>> 49² = 2401
-
-
d) Cuadrado de los números de
dos cifras acabados en 2 (y de las demás cifras del 3 al 8):
De una manera similar a los acabados
en 1, haremos los acabados en 2: "Cuadrado de
la decena, el doble de la decena por 2, añadimos un 4 (cuadrado
del 2)"
-
Ej:
22²: cuadrado de la decena 2
x 2 = 4
el doble de la decena 2 + 2 = 4 por 2 = 8
le añadimos un 4 >>>> y obtenemos el 484 = 22²
Ej: 52²:
cuadrado de la decena 5 x 5 = 25
el doble de la decena 10 por 2 = 20, es decir, nos llevamos 2, por
tanto, 25+2 = 27 >> 270
le añadimos un 4 >>>> y obtenemos el 2704 = 52²
-
El método se puede generalizar
para los demás números.
-
Para acabar veamos los números
acabados en 3: "Cuadrado de la decena, el doble
de la decena por 3, añadimos un 9 (cuadrado del 3)"
-
Ej. 73²: cuadrado de la decena 7 x
7 = 49
el doble de la decena 7 + 7 = 14 por 3 = 42, nos llevamos 4, por
tanto, 49+4 = 53 >> 532
le añadimos un 9 >>>> y obtenemos el 5.329 = 73²
EJERCICIO: Calcular con este método los siguientes números
al cuadrado:
35² = ... ; 41² = ... ;
32² = ... ; 75² = ... ;
59² = ... ; 115² = ...
(solución)

Método
de los "productos equidistantes"
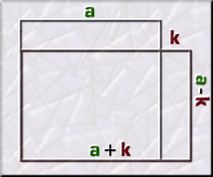 Un aspecto interesante de los
números
al cuadrado es la "pérdida" que se produce si aumentamos y disminuimos
los números
en una cantidad constante, es decir, la diferencia de área entre
cuadrados y rectángulos con un mismo perímetro.
Un aspecto interesante de los
números
al cuadrado es la "pérdida" que se produce si aumentamos y disminuimos
los números
en una cantidad constante, es decir, la diferencia de área entre
cuadrados y rectángulos con un mismo perímetro.
Tomamos un cuadrado de lado a y
lo convertimos en un rectángulo de lados: a
+
k y
a
-
k.
Veamos
lo que ocurre con un ejemplo numérico: 24²
= 576
>
25 x 23 = 575 (-1)
Hemos sumado y restado 1 y la distancia es 1²
>
26 x 22 = 572 (-4)
Hemos sumado y restado 2 y la distancia es 2²
>
27 x 21 = 567 (-9)
Hemos sumado y restado 3 y la distancia es 3²
>
28 x 20 = 560 (-16)
Hemos sumado y restado 4 y la distancia es 4²
> 29 x 19 = 551 (-25)
Hemos sumado y restado 5 y la distancia es 5²
Podemos concluir, por tanto, que:
"La diferencia
entre el área de un cuadrado y el área de un rectángulo,
generado a partir de aquel, es igual al cuadrado de la deformidad aplicada"
De aquí también se puede
sacar una aplicación numérica en el cálculo rápido
del producto de números que sean equidistantes a un número
al cuadrado, así, si observamos que 18 y 12 son equidistantes al
15, podremos calcular muy rápidamente 18 x 12, dado que 15²
= 225 y la distancia
es 3² = 9,
deducimos que 18 x 12 = 216.
Sólo
se puede aplicar cuando ambos factores son pares o ambos son impares.
Este "método de los productos equidistantes" es muy eficaz con la
sola condición de memorizar una buena serie de números al
cuadrado y de observar rápidamente si un producto lo permite o no.
EJERCICIO: Calcular con este método aquellos productos que permitan
su aplicación:
29 x 21 = ... ; 35 x 30 = ... ; 18 x 12 = ... ; 23 x 31 = ... ; 37 x 32
= ... ; 54 x 46 = ...
(solución)

TRIÁNGULOS PITAGÓRICOS
ENTEROS
Expresiones matemáticas
para obtener triángulos rectángulos con valores enteros
-
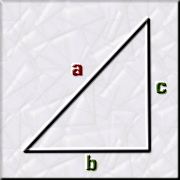 El gran Pitágoras de Samos nos legó su archiconocido Teorema
de los triángulos rectángulos, pilar fundamental de cálculos
geométricos y trigonométricos, en el que se relacionan las
medidas de los catetos y de la hipotenusa: a²
= b² + c²
El gran Pitágoras de Samos nos legó su archiconocido Teorema
de los triángulos rectángulos, pilar fundamental de cálculos
geométricos y trigonométricos, en el que se relacionan las
medidas de los catetos y de la hipotenusa: a²
= b² + c²
-
Dado que al aplicar esta fórmula matemática hemos de acabar
calculando una raíz cuadrada, casi siempre nos encontraremos que
no obtenemos valores exactos, o mejor dicho, valores enteros.
Al propio Pitágoras le debemos el triángulo rectángulo
arquetipo de medidas 3, 4 y 5, pero si lo que pretendemos
es utilizar otros triángulos rectángulos con valores enteros
casi nunca lo conseguiremos y acabaremos recurriendo a este triángulo
pitagórico (3, 4, 5) o a sus múltiplos.
Dedico esta sección a exponer unas expresiones matemáticas
que
nos permitirán obtener la mayoría de los triángulos
rectángulos de valores enteros que existen, son el fruto de una
buena idea inicial y de un estudio exhaustivo posterior. Así que
podéis tomar buena nota y, de este modo, tener una pequeña
herramienta con la que podréis generar problemas, etc. que tengan
por solución siempre valores enteros, o simplemente ver este capítulo
como una curiosidad matemática más.
-
La primera expresión nos genera las 3 medidas de triángulos
rectángulos en que el cateto pequeño es un número
impar:
2n
+ 1, 2n(n + 1),
2n²
+ 2n + 1
-
Así para n = 1 obtenemos los valores: 3,
4 y 5
(¿os
suena de algo?). Para n = 2: 5,
12,
13,
etc.
-
La segunda expresión nos genera las 3 medidas de triángulos
rectángulos en que el cateto pequeño es un número
par:
2(n
+ 1), n(n + 2),
n²
+ 2n + 2
-
Ej. para n = 1 obtenemos los valores: 4,
3
y 5 (otra
vez). Para n = 3: 8,
15,
17,
etc.
Veamos una tabla con los 7 primeros valores de cada una:
-
-
|
2n + 1
|
2n(n + 1) |
2n²
+ 2n + 1 |
n
|
2(n
+ 1) |
n(n
+ 2) |
n²
+ 2n + 2 |
|
3 |
4 |
5 |
1 |
4 |
3 |
5 |
|
5 |
12 |
13 |
2 |
6 |
8 |
10 |
|
7 |
24 |
25 |
3 |
8 |
15 |
17 |
|
9 |
40 |
41 |
4 |
10 |
24 |
26 |
|
11 |
60 |
61 |
5 |
12 |
35 |
37 |
|
13 |
84 |
85 |
6 |
14 |
48 |
50 |
|
15 |
112 |
113 |
7 |
16 |
63 |
65 |
-
A las dos expresiones expuestas
tendríamos que añadir una constante k, que al multiplicarla
por cada uno de los valores obtenidos y tomando diferentes valores nos
permita obtener los múltiplos de estas medidas, que obviamente,
también cumplen el Teorema de Pitágoras:
-
[2n
+ 1, 2n(n + 1), 2n²
+ 2n + 1] · k
[2(n
+ 1), n(n + 2), n²
+ 2n + 2] · k
-
Ahora ya tenéis un buen puñado de ejemplos y con las expresiones
matemáticas podréis obtener más.
De todas formas estos no son los únicos
y, por eso, acabé por buscar otro algoritmo de cálculo aún
más general.
Partiendo de la conocida regla, expuesta
en el capítulo anterior, que dice que:
-
"La distancia entre 2 números cualquiera al cuadrado es la
suma por la diferencia"
x² - y²
= (x + y) · (x - y)
-
Se puede hacer la siguiente demostración:
Si tenemos un número a, que es múltiplo de otros,
lo podremos expresar como a = x · y
Según
el Teorema de Pitágoras: a²=
c²
-
b²
= (c + b) · (c - b)
De aquí podemos deducir que: x² · y² =
(c + b) · (c - b), y por tanto:
x²
= c + b
y² = c - b Si
ahora resolvemos este sistema de ecuaciones tendremos que:
-
c
=
(x²
+ y²) / 2 , b =
(x² - y²) / 2
, a = x · y
-
O sea, que dado un cateto que mide a lo
podremos expresar en forma de producto de dos divisores: x · y (incluso
los números primos: a = a · 1 => x = a, y = 1, cumplen
esta fórmula => ver la tabla) y a partir de estos
hallamos que: el otro
cateto es la mitad de la diferencia de los cuadrados de sus divisores y su hipotenusa
es la mitad de la suma de los cuadrados de sus divisores.
-
El único pequeño problema que surge aquí es que al
tener que dividir por 2 en algunos casos (si un divisor es par y
el otro impar) no salen valores exactos, pero sus múltiplos pares
sí que lo serán y, en cualquier caso, como máximo
tendremos un decimal .5 igualmente muy interesante.
Veamos ahora unos cuantos ejemplos:
-
-
|
a = x · y |
b=
(x² - y²) / 2 |
c=
(x² + y²) / 2 |
a = x · y |
b=
(x² - y²) / 2 |
c=
(x² + y²) / 2 |
|
27 = 9 · 3 |
(9² - 3²) / 2 =
36 |
(9² + 3²) / 2 =
45 |
45 = 15 · 3 |
(15² - 3²) / 2 =108 |
(15² + 3²) / 2 =117 |
|
32 = 8 · 4 |
(8² - 4²) / 2 =
24 |
(8² + 4²) / 2 =
40 |
48 = 8 · 6 |
(8² - 6²) / 2 =
14 |
(8² + 6²) / 2 =
50 |
|
33 = 11 · 3 |
(11² - 3²) / 2 =
56 |
(11² + 3²) / 2 =
65 |
17 = 17 · 1 |
(17² - 1²) / 2 =144 |
(17² + 1²) / 2 =145 |
|
35 = 7 · 5 |
(7² - 5²) / 2 =
12 |
(7² + 5²) / 2 =
37 |
36 = 9 · 4 |
(9² - 4²) / 2 = 32.5 |
(9² + 4²) / 2 = 48.5 |
En este último ejemplo tenemos
que a =
36, b =
32.5, c =
48.5, de aquí podemos deducir que sus múltiplos
pares sí son enteros como: a =
72, b =
65, c =
97, a =
144, b =
130, c =
194, etc.
-
Hasta aquí este estudio, para
concluir sólo diré que todavía queda un grupo de triángulos
rectángulos de valores enteros que no se generan con ninguna de
las expresiones expuestas, pero sí que con ellas obtendremos la
mayoría de los que existen y, por tanto, me parecen de gran utilidad.
- Cálculo
de la diagonal de una figura geométrica que no existe!
-
- Si queremos calcular lo que mide la
diagonal de un cuadrado conociendo lo que miden sus lados, sólo
necesitaremos aplicar el Teorema de Pitágoras.
Así un cuadrado de lado 1,
tendrá una diagonal que mide V¯2¯
(raíz
cuadrada de 2)
A partir de aquí deduciremos
que la diagonal de un cuadrado de lado n mide: d
=n · V¯2¯
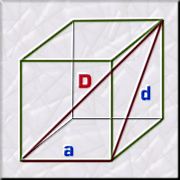
Si ahora queremos
calcular lo que mide la diagonal de un cubo, entre dos vértices
de caras opuestas, también podremos aplicar el Teorema de Pitágoras
si triangulamos el cubo y observamos el triángulo rectángulo
formado por una arista inferior a,
la diagonal de la cara lateral d
y la diagonal grande D.
Así observaremos
que D² =
a² + d²
En el caso del cubo de arista a = 1
la diagonal lateral d = V¯2¯
y, por tanto:D² =
1² + (V¯2¯)²
= 1 + 2 = 3 => D = V¯3¯
Obviamente podremos afirmar que la diagonal grande de un cubo de lado n
mide: D =n · V¯3¯
- Con
todo esto, y si seguimos este procedimiento de triangulación, podríamos
calcular cuanto miden las diagonales de figuras geométricas de más
de 3 dimensiones, es decir, de figuras que no existen, ni podemos tampoco
imaginar dada nuestra limitación tridimensional.
La diagonal
grande de una figura tipo cubo, pero de 4 dimensiones, será: D
= n · V¯4¯ = 2n
La diagonal grande de una figura tipo cubo, pero de 5 dimensiones, será: D
= n · V¯5¯, etc.
- ¡Qué
magnífico poder calcular algo que no podemos ni siquiera imaginar
su forma! ¡Me maravilla que una ciencia como las matemáticas
pueda llegar dónde no lo hace ni la imaginación!
Como me gustaría
llegar a un mundo cuatridimensional y pedir a sus habitantes que me mostrasen
un dado y observar este objeto en que su diagonal mide el doble que sus
aristas...

MÚLTIPLOS y DIVISORES
Criterios de divisibilidad
Todo número no 'primo' es el producto de dos o más factores
o divisores, y por lo tanto, puede ser expresado como un producto de dos
cifras:
121
= 11 x 11 ; 480 = 80 x 6, etc. ; 989
= 43 x 23 ...
Existen ciertos criterios de divisibilidad que de forma sencilla nos pueden
ayudar a conocer rápidamente algunos divisores de un número
dado. Veamos unos cuantos, algunos de ellos muy conocidos:
- Todos
los números pares son divisibles por 2.
- Un número
es múltiplo de 3 -o lo tiene por divisor- si la suma de sus cifras
es múltiplo de 3.
(es decir, pertenece a la tabla del 3)
Ej.
861 => 8 + 6 + 1 = 15 (si) ; 563 = 5 + 6 + 3 = 14 (no)
- Son
divisibles por 4 los números en los que las 2 últimas cifras
son múltiplo de 4 -o bien sean 00
Ej.
764, 348, 920, etc.
- Los
números acabados en 5 ó en 0 son divisibles por 5.
- Un número
es divisible por 6 si también lo es por 3 y por 2.
- Un número
es divisible por 9 si la suma de sus cifras es múltiplo de 9.
Ej.
702, 855, 378, 144, etc.
- Todos
los números acabados en 0 son múltiplos de 10, lógicamente.
- Un número
es divisible por 12 si también lo es por 3 y por 4, es decir, si
la suma de sus cifras
es múltiplo de 3 y las 2 últimas cifras son múltiplo
de 4.
Ej.
648 > 6 + 4 + 8 = 36 y
48
es múltiplo de 4 (si)
375 > 3 + 7 + 5 = 18, pero 75 no es múltiplo de 4
(no)
- Un número
es divisible por 15 si también lo es por 3 y por 5, es a decir,
si la suma de sus cifras
es múltiplo de 3 y acaba en 5 ó en 0.
Ej.
645 > 6 + 4 + 5 = 15 y
acaba en 5 (si)
575 > 5 + 7 + 5 = 17 (no)
- Un número
es divisible por 20 si es par y acaba en 0.
- Un número
es divisible por 25 si acaba en 25, en 50, en 75 ó en 00.
Estos son los casos más sencillos, ahora algunos criterios menos
conocidos:
- Un número
es múltiplo de 11:
· Si la suma de las cifras extremas es menor que 10 e igual
a la central (3 cifras)
Si las cifras tomadas de 2 en 2 dan 2 resultados iguales (más de
3 cifras)
Si restamos a las cifras extremas el número central y sale 0 o un
múltiplo de 11.
Ej.
253 (si), 891 (si), 748 (si), 567 (no)
Entonces podemos saber cuál es el otro divisor ya que éste
es igual a las 2 cifres de los extremos, si sale 0, o bien, restamos una
decena si sale 11, etc.
Ej.
891 > 8 + 1 = 9 ó 8 + 1 - 9 = 0; 891
=
11 x 81; 253
=
11 x 23
627 > 6 + 7 = 13 - 2 = 11; 627
= 11 x 57
1.782 > 7 + 2 = 8 + 1; 1.782
= 11 x 162
Los
múltiplos de 11 que sean pares son múltiplos de 22"
- Un número
es múltiplo de 7:
Si
al sumar el doble de la centena a las 2 últimas cifras del número
se obtiene un múltiplo de 7.
(se han de
reconocer los múltiplos de 7 hasta el 100). Es un criterio ideal
para números no muy grandes)
Ej.
437 (no) > 4 x 2 + 37 = 45 (que no lo es)
651 (si) > 6 x 2 + 51 = 63 (7 x 9); 651 = 7 x 93
Si al restar, sucesivamente, el doble de la última cifra (unidades)
del número se obtiene un múltiplo de 7
Ej.
6.251 > 625 - 1 x 2 = 623 > 62 - 2 x 3 = 56
(si
lo es)
3.474 > 347 - 4 x 2 = 339 > 33 - 9 x 2 = 15
(no
lo es)
- Un número es múltiplo
de 14:
Si es par y al sumar el doble de la centena a las 2 últimas cifras
obtenemos un múltiplo de 7.
- Un número es múltiplo
de 8:
· En centenas pares si las 2 últimas cifras son un
múltiplo de 8.
· En centenas impares si las 2 últimas cifras son múltiplo
de 4, pero no de 8.
Ej.
464 (si); 744 (si); 932 (no); 684 (no); 584
(si)
Otro criterio aplicable también
a los múltiplos de 8, pero algo menos claro, es:
Son divisibles
por 8 los números en los que las 3 últimas cifras son múltiplo
de 8 o acaban en 000
- Un número
es múltiplo de 13:
Si al restar 4 veces la centena a les 2 últimas cifras del número
se obtiene un múltiplo de 13 (<100)
Ej.
364 > 64 - 3 x 4 = 52, (52 = 13 x 4) (si)
Ej.
475 > 75 - 4 x 4 = 59, (no)
- Un número
es múltiplo de 17:
Si al restar
el doble de la centena a las 2 últimas cifras del número,
tenemos un múltiplo de 17(<100)
Ej.
578 > 78 - 5 x 2 = 68, (68 = 17 x 4) (si)
Ej.
832 > 32 - 8 x 2 = 16, (no)
- Un número
es múltiplo de 16:
Si podemos hacer su mitad durante 4 veces seguidas y siempre sale un número
entero.
Ej.
448 > 224 > 112 > 57 (si)
Ej.
728 > 364 > 182 > 91 (no)
- A título
de curiosidad diré que:
Cualquier número con las 3 cifras repetidas es múltiplo de
37.
de hecho es 37 por la suma de las 3 cifras (o por el triple de las centenas):
Ej.
555 = 37 x 15; 888 = 37 x 24
Existen otros e, incluso, el lector podría diseñar alguno
propio...

"Múltiplos
sinceros"
He denominado "múltiplos sinceros" a:
"Los números que son múltiplos de un número y en los
cuales la suma de sus cifras es también este mismo número".
(Haciendo
una suma, no volviendo a sumar el resultado de la suma de sus cifras)
Ej. el 24 es
"múltiplo sincero" del 6, el
144
es "múltiplo sincero" del
9, el
511
lo es del 7,
etc.
Todos los números tienen 'múltiplos sinceros', de hecho constituyen
un subconjunto del conjunto total de los múltiplos del número.
Se acepta el propio número como el primer elemento de cada subconjunto.
Veamos un pequeño estudio sobre los primeros "múltiplos sinceros"
de cada número:
El 2 no tiene muchos múltiplos sinceros dado que es un número
muy bajo:
M.S. del 2 = { 2, 20, 110, 200, 1.010, 1.100,
2.000, ...}
(Distancia clave 90, ...)
M.S. del 3 = { 3, 12, 21, 30, 102, 111, 120,
201, 210, 300, ...} (Distancia
clave 9, ...)
M.S. del 4 = { 4, 40, 112, 220, 400, 1.120,
2.020, 2.200...}
M.S. del 5 = { 5, 50, 140, 230, 320, 410,
500, 1.040 ...}
(Distancia clave 90, ...)
M.S. del 6 = { 6, 24, 42, 60, 114, 132, 150,
204, 222, 240, ...} (Distancias
claves 18, 54,...)
M.S. del 7 = { 7, 70, 133, 322, 511, 700,
2.023, 2.212, 2.401, ...} (Distancia
clave 189, ...)
M.S. del 8 = { 8, 80, 152, 224, 440, 512,
800, 1.016...}
(Distancia clave 72, ...)
M.S. del 9 = { 9, 18, 27, 36, 45, 54, 63,
72, 81, 90, 108, 117, ...} (Distancia
clave 9, ...)
M.S. del 10 = { 10, 190, 280, 370, 460, 550,
640, 730, 820, ...} (Distancia
clave 90, ...)
Los 'múltiplos sinceros' del 11 os los propongo como ejercicio y
doy la solución al final de esta página.
M.S. del 12 = { 48,
84, 156, 192, 228, 264, 336, 372, 408, 444, ...} (Distancies
claves 36, 72, ...)
M.S. del 13 = { 247,
481, 715, 1.183, 1.417, 1.651, ...}
(Distancia clave 234, ...)
M.S. del 14 = { 266, 518, 770, 1.274, 1.526,
2.282, ...}
(Distancia clave 252, ...)
M.S.
del 15 = { 195, 285, 375, 465, 555, 645, 735,
825, 915...} (Distancia
clave 90, ...)
El número que tiene mas densidad de múltiplos sinceros es
el 9, de hecho todos sus múltiplos hasta el 90 lo son.
En cambio el 11, hasta podría parecer que no tiene ...
También se puede observar que la distancia entre "múltiplos
sinceros" es bastante constante para cada número, la más
frecuente es 90 y, en todos los casos, son siempre múltiplos de
9, precisamente el número con más 'múltiplos sinceros'.
Este estudio, probablemente, llegaría hasta el infinito ...
Si os ha gustado el tema os propongo calcular los primeros 'múltiplos
sinceros' del 16 y del 17.
(Solución)

Números
"perfectos", "casi-perfectos" y números "amigos"
Un tema
muy conocido de los matemáticos es el de los 'números perfectos',
denominados así, porque:
"La
suma de todos sus divisores, excepto él mismo, es igual al propio
número".
El menor 'número perfecto' es
el 6, que tiene por divisores el 1, 2, 3, (6), como podemos ver se cumple
que: 1 + 2 + 3 = 6.
Los 'números casi-perfectos' son aquellos que:
"La
suma de todos sus divisores, excepto él mismo, es una unidad inferior
al propio número"
Son
'números casi-perfectos' todas las potencias de 2, como se
puede comprobar fácilmente.
Ej. El 4 tiene por divisores
el 1, 2, (4), como podemos ver se cumple que: 1 + 2 = 3.
(Div 8) =
{ 1, 2, 4, (8)} 1 + 2 + 4 = 7. (Div 16) = { 1, 2, 4, 8, (16)} 1
+ 2 + 4 + 8 = 15, etc.
Podemos decir que dos números son 'amigos' cuando:"La suma
de todos los divisores de cada número, excepto ellos mismos, es
igual al otro número".
Sin
duda un concepto, digamos que muy romántico, imaginar números
que son amigos unos de otros, pero, en cualquier caso, un divertimento
interesante el encontrarlos.
Ej. El 220 y el 284 son números amigos, dado que:
(Div
220) = { 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, (220)} 1 + 2 +
4 + 5 + 10 + 11 + ... = 284.
(Div 284) = { 1, 2, 4, 71,
142, (284)} 1 + 2 + 4 + 71 + 142 = 220.

SOLUCIONES:
54² =
2.916 (2.500
+ 104 x 4 = 2.916)
41²
- 26² = (41 + 26) x (41 - 26) = 67 x 15 = 1.005
35² = 1.225
(3 x 4 = 12, 25)
41² = 1.681 (4²
= 16, 4 x 2 = 8, 1)
32² = 1.024 (3²
= 9, 3 x 2 x 2 = 12, 2² = 4) >> 9 +1 = 10, 2, 4 >> 1.024
75² = 5.625 (7
x 8 = 56, 25)
59² = 3.481 (6²
= 36, 6 x 2 = 12, 1) >> 360 - 12 = 348, 1 >> 3.481
115² = 13.225 (11 x 12 =
132, 25)
29 x 21 = 25² - 4² = 625 - 16 = 609
35 x 30 = 1.050 (no)
18 x 12 = 15² - 3² = 225 - 9 = 216
23 x 31 = 27² - 4² = 729 - 16 = 713
37 x 32 = 1.184 (no)
54 x 46 = 50² - 4² = 2.500 - 16 = 2.484
M.S. del 11 = { 209, 308, 407, 506, 605, 704,
803, 902, ...} (Distancia
clave 99, ...)
M.S. del 16 = { 448, 736, 2.176, 2.464, 2.752,
...}
(Distancia clave 288, ...)
M.S. del 17 = { 476, 629, 782, 935, 1.088,
1.394, ...} (Distancia
clave 153, ...)
(índice)

Volver al índice
Autor: Blai Figueras Álvarez

E-mail:
mentaludix@hotmail.com

 LOS FASCINANTES CUADRADOS MÁGICOS
LOS FASCINANTES CUADRADOS MÁGICOS EL MARAVILLOSO TRIÁNGULO ARITMÉTICO
EL MARAVILLOSO TRIÁNGULO ARITMÉTICO
![]() NÚMEROS AL CUADRADO
NÚMEROS AL CUADRADO

![]() TRIÁNGULOS PITAGÓRICOS
TRIÁNGULOS PITAGÓRICOS![]() MÚLTIPLOS y DIVISORES
MÚLTIPLOS y DIVISORES
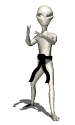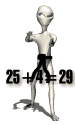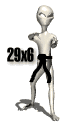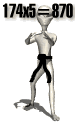
 PRODUCTOS ALTERNATIVOS
PRODUCTOS ALTERNATIVOS

 DECIMALES PERIÓDICOS
DECIMALES PERIÓDICOS
 RAÍCES SORPRENDENTES
RAÍCES SORPRENDENTES

 CUADRADOS INTERCALADORES
CUADRADOS INTERCALADORES
 CASTELLERS NUMÉRICOS
CASTELLERS NUMÉRICOS

 TRANSBASES
TRANSBASES
 POTENCIAS
CURIOSAS
POTENCIAS
CURIOSAS 
 GEOMETRIZANDO
GEOMETRIZANDO

 NÚMEROS
TRASCENDENTES
NÚMEROS
TRASCENDENTES
 POESÍA AL NÚMERO
p
POESÍA AL NÚMERO
p SISTEMA MNEMOTÉCNICO PARA NÚMEROS
SISTEMA MNEMOTÉCNICO PARA NÚMEROS 
![]() PASATIEMPOS y ACTIVIDADES
PASATIEMPOS y ACTIVIDADES
![]() CHANZAS MATEMÁTICAS
CHANZAS MATEMÁTICAS
![]() MATEJUEGOS
MATEJUEGOS
 Un aspecto interesante de los
números
al cuadrado es la "pérdida" que se produce si aumentamos y disminuimos
los números
en una cantidad constante, es decir, la diferencia de área entre
cuadrados y rectángulos con un mismo perímetro.
Un aspecto interesante de los
números
al cuadrado es la "pérdida" que se produce si aumentamos y disminuimos
los números
en una cantidad constante, es decir, la diferencia de área entre
cuadrados y rectángulos con un mismo perímetro.
 El gran Pitágoras de Samos nos legó su archiconocido Teorema
de los triángulos rectángulos, pilar fundamental de cálculos
geométricos y trigonométricos, en el que se relacionan las
medidas de los catetos y de la hipotenusa: a²
= b² + c²
El gran Pitágoras de Samos nos legó su archiconocido Teorema
de los triángulos rectángulos, pilar fundamental de cálculos
geométricos y trigonométricos, en el que se relacionan las
medidas de los catetos y de la hipotenusa: a²
= b² + c²

