Siempre he hallado un notable placer, digamos
intelectual, al resolver problemas de todo tipo, especialmente lógicos
y numéricos, creo que han sido la base para desarrollar o mejorar
algunas de mis habilidades.
Pues bien, últimamente he descubierto
que es, probablemente, aún más divertido y motivador para
mi crear problemas o ejercicios, dado que en muchos casos puede llegar a
ser más imaginativo y complejo...
Por tanto os propongo una serie de problemas
matemáticos que os pueden complicar un poco la vida o hacérosla
más agradable!

CRIPTOGRAMAS
JEROGLÍFICOS
MATEMÁTICOS
LOS GEMELOS
ALÍCIA PER SECULA...
LOS HEXÁGONOS
LA LÚNULA
LA ECUACIÓN IMPOSIBLE
HEXÁMEROS
OPERACIONES INVEROSÍMILES
LOS SEIS EUROS
ARCO OJIVAL
ESCAQUEANDO
LA ESTRELLA DE OCHO PUNTAS

CRIPTOGRAMAS
Los criptogramas son operaciones de cálculo en las cuales se han
sustituido las cifres por letras u otros símbolos de manera que
se propone encontrar que valor corresponde a cada letra, teniendo en cuenta,
claro, que una misma letra no puede representar dos valores numéricos
diferentes.
·
CRIPTOGRAMA NAVIDEÑO
Probablemente más de uno ya estará
pensando en las próximas vacaciones de Navidad, yo también
:-), así que he pensado una manera original de desearos unas buenas
fiestas.
Las letras sustituyen a los números
del 0 al 9. ¿Seréis capaces de hallar esta suma navideña?
Nota: La traducción del catalán sería "ES NAVIDAD
BUENAS FIESTAS"
(solución)
·
CRIPTOGRAMA MILITAR
Estamos viviendo unos años de grandes controversias
internacionales, yo no pretendo tomar partido por ningún otro posicionamiento
político que el de pedir la Paz para todos los pueblos y naciones
de la Tierra.
Pero para desdramatizar esta situación,
y, por supuesto, en tono humorístico, os propongo resolver este
criptograma (¿anti USA?)
(solución)

JEROGLÍFICOS
MATEMÀTICOS
Cuando era niño mi padre me hacía
una "bromita" matemática, que quizás algunos ya conozcan.
Si yo le decía: -"Papa,
tinc set!"
(Papá, tengo sed!)
set = 7
Él me contestaba: - "Doncs el
càntir és buit, perquè
és nou i encara es deu!"
(vuit = 8, nou=9, deu = 10)
(Pues el botijo estávacío,
porque es nuevo y
todavía se debe!)
Años más tarde yo vivía
en Andújar (Jaén), y en algunas ocasiones que estaba de tapeo
con mis amigos, se había producido la siguiente situación
en algún bar:
Cuando a la hora de pagar llegaba el camarero
y se le pedía la cuenta: - "¿Cuánto es?"
Si él respondía: - "Setesientas"
(En Andújar todo el mundo sesea, es decir, pronuncia s por c)
El gracioso de turno le replicaba: - "¿Y
si me quedo de pie?"
(obviamente por: "Si te sientas")
Estos son algunos ejemplos de carácter,
digamos, popular.
Yo ahora os propondré unos jeroglíficos,
de creación propia, generados exclusivamente con símbolos
u operaciones matemáticas.
(Obviamente se ha de considerar más
el aspecto fonético y, por tanto, me he permitido algunas faltas
ortográficas y gramaticales)
1. El primero fue una improvisación que tuve
durante una clase sobre los números enteros en el año 1999:
(Respuesta en catalàn)
2. Últimamente se ha puesto de moda el
spanglish, o sea, la mezcla del español y el inglés, pues
yo me apunto y os propongo este otro jeroglífico que se responde
en este popurri del lenguaje. (¡Sed imaginativos!)
|
10 + 2
|
|
¿Cómo te gustan los films?
|
3. El siguiente jeroglífico se podría
considerar una llamada a ¡la prudencia en carretera! (Respuesta
en catalàn)
|
170 an
|
|
Com t'agraden els vehicles?
|
4. El siguiente jeroglífico se lo dedico
a un par de compañeros míos. (Respuesta
en catalàn)
|
2 + 3 3a i 6
7
|
|
Qui són els afortunats?
|
5. Hasta frases enteras y largas podríamos
crear sólo con números y símbolos matemáticos,
veamos un ejemplo: (Respuesta en catalàn)
|
1 101 e1000 i ·
2 6>7 101010 lim(a + i - ab)
|
|
Què li ha dit el metge?
|
(soluciones)

LOS
GEMELOS
Estamos dentro de una habitación en la
cual hay dos puertas cerradas, una es la salida y la otra lleva a la desgracia.
Obviamente desconocemos cuál es la buena y cuál la mala.
También hay dos hermanos gemelos, uno
que siempre dice la verdad y el otro que es absolutamente mentiroso, desgraciadamente
tampoco sabemos quién es sincero y quién es falso.
Sólo podemos hacer una pregunta a uno
de los dos hermanos para tratar de escapar.
· ¿Qué
pregunta haríais vosotros para hallar la salida?
· ¿Cuál sería, pues, la
salida hacia la salvación?
(solución)

ALICIA
PER SECULA...
Puede que muchos de vosotros hayáis leído
el clásico de Lewis Carroll "Alicia en el País de las Maravillas",
pero lo que probablemente no habréis advertido es la presencia de
algunas cuestiones matemáticas geniales, propias de la privilegiada
mente de su autor, que era profesor y entre sus aficiones estaban la criptografía
y el ajedrez.
Aquí os presento un texto de esta obra:
"¡Ay, Dios mío,
qué rompecabezas es todo esto! Voy a probar si sé todas las
cosas que acostumbraba saber. Veamos: cuatro por cinco, doce, y cuatro
por seis, trece...
¡Ay, Dios mío, así nunca llegaré
a veinte!"
Supongo que muchos lectores han creído que estas palabras
eran propias de una tontería infantil de Alicia, pero en realidad
esconden una cuestión matemática fantástica y bastante
compleja.
- ¿Como creéis que
está contando Alícia?
- ¿Es posible que llegue
a veinte siguiendo esta lògica?
Os garantizo que si no reflexionáis detenidamente
esta cuestión, puede que os llevéis una gran sorpresa...
(solución)

LOS
HEXÁGONOS
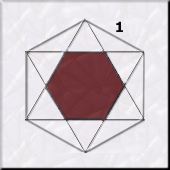
He aquí un problema geométrico
muy interesante tanto por su ejecución como por su solución:
Hay que hallar la relación
existente entre los dos hexágonos, el mayor de arista 1 y el menor
que queda en el centro de la estrella de seis puntas.
(solución)

LA
LÚNULA
Uno de los tres grandes problemas matemáticos de
la antigüedad era la "Cuadratura del círculo",
que consistía en hallar un cuadrado con la misma área de
un círculo dado.
Esto que, de entrada, puede parecer
relativamente sencillo, no lo es en absoluto si tenemos en cuenta que los
geómetras griegos eran completamente puristas y sólo permitían
utilizar la regla y el compás.
Obviamente la resolución numérica
de este problema es relativamente fácil, pero desde el punto de
vista geométrico llevó de cabeza a los mejores matemáticos
durante más de 2.000 años, hasta que en el siglo XIX se demostró
que era una cuestión irresoluble. ¡¡Pobrecitos si lo
llegan a saber!!

Un de los que lo investigó
intensamente fue Hipócrates de Quíos, quién durante
uno de sus numerosos estudios al respecto diseñó esta figura
denominada "lúnula".
Yo os propongo la siguiente cuestión:
Calculad el área de esta
lúnula, teniendo en cuenta que la base y la altura del triángulo
generador es, por ejemplo, una unidad.
Sin duda un problema curioso...
(solución)

LA
ECUACIÓN IMPOSIBLE
"Hace muchos
años me plantearon resolver una ecuación muy atípica
y he creido que podría ser una buena manera de torturaros si es
que todavía aguantáis 'on line', incluso haré un pequeño
regalo a aquellos que se tomen la molestia de resolverla."
Se trata de encontrar
los cuatro números menores que cumplen una igualdad del tipo siguiente:
xª
+ yª = zª + wª = N
Si
a
= 1, es decir, para la potencia
1, tenemos que:
1
+ 4 = 2 + 3 = 5
Si a = 2: Hallar
los cuatro primeros números que resuelven la ecuación:
x²
+ y² = z² + w² = N
(os
la dejo calcular, pero podéis ver la solución
en esta página)
Yo os propongo calcular esta igualdad si a = 3, es decir, para la
potencia 3.
Hallad los cuatro números menores y el resultado N, que cumplen:
x³
+ y³ = z³ + w³ = N
-
-
Un amable lector, Antonio López Vivar,
ha creado una aplicación llamada "Calculador" que permite resolver este
problema para cualquier exponente -si es factible, claro. Así, ha dado las
soluciones para las potencias tercera y cuarta.
-
Si lo deseáis os podéis descargar este programa de
cálculo, lo he incluido en el apartado de las soluciones.
(soluciones)

OPERCIONES
INVEROSÍMILES
A veces encontramos problemas de cálculo que pueden ser tan sencillos,
pero con una apariencia tan terrorífica, que podríamos creer
que el que los plantea se ha vuelto majareta...
Pues quizás sí, pero, en cualquier caso, os propongo que
calculéis, sin ayuda de la calculadora, el siguiente par de ecuaciones:
x
= 582.437.123² - (582.437.124 x 582.437.122)
x
= 756.902.438² - (756.902.440 x 756.902.436)
Dada la inmensidad de estos números os puede desconcertar en principio,
si queréis una pequeña ayuda os recomiendo que consultéis
el artículo dedicado a las curiosidades titulado:
Distancia
entre los números al cuadrado
(solución)

HEXÁMEROS
Os
propongo ahora un par de ejercicios de cálculo basados en el juego
"Cifras + Letras"
Con
las 6 cifras dadas alrededor, tenéis que encontrar el número
de 3 cifras propuesto en el centro de los "Hexámeros"
Se pueden utilizar las 4 operaciones aritméticas, es a decir, suma,
resta, producto o división.
No es necesario hacer uso de todas las cifras, pero sólo se pueden
utilizar una vez, es decir, no se puede repetir ninguna.
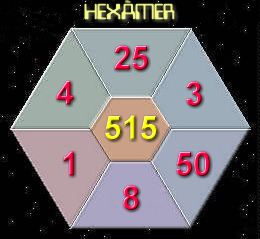
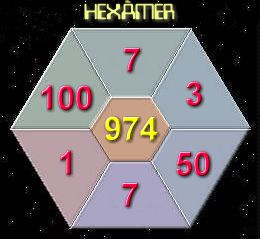
Ambos
problemas tienen, al menos, una solución exacta, por mucho que os
pueda parecer imposible!!
(solución)

ARCO
OJIVAL
Los arcos
ojivales fueron una evolución arquitectónica que se produjo
en la transición del románico al gótico, se emplearon
en las fachadas, puertas, etc. a menudo incluyendo un rosetón con
vidrieras, etc.
Al ser combinados
con las bóvedas se resolvió un problema típico de
los arcos de medio punto, que era el no permitir la unión de dos
pilares de diferente altura. Los arcos ojivales, en cambio, si lo permiten,
ya que para nivelar dos pilares de diferente altura sólo será
necesario ajustar la amplitud de las ojivas del techo.
Un arco ojival
es la intersección de los cuadrantes de dos círculos con
el mismo radio situados uno a cada lado, de hecho la amplitud de la ojiva
es igual al radio de estos círculos generadores.
Es decir, imaginemos
un cuarto de círculo a la derecha que se cruza con otro cuarto de
círculo con el mismo radio a la izquierda, la zona de intersección
delimita un arco ojival. ¡Qué cosas sabían en la Edad
Media!
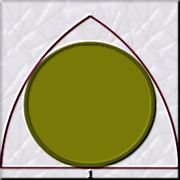 No
nos trasladaremos a la Edad Media, pero sí que os plantearé
unas cuestiones en relación a los arcos ojivales:
No
nos trasladaremos a la Edad Media, pero sí que os plantearé
unas cuestiones en relación a los arcos ojivales:
· Calculad
el área del arco ojival teniendo en cuenta que su amplitud, o sea,
los radios de los círculos generadores es 1.
· Calculad
el área del círculo menor, la roseta, contenido en él.
·
Finalmente, imaginad cualquiera de los dos círculos generadores
de la ojiva y calculad cuantos círculos menores, rosetas, se pueden
incluir exactamente.
(solución)

LOS
SEIS EUROS
 Ya tenemos el euro en casa!!
Ya tenemos el euro en casa!!
Y a pesar de las dificultades de adaptación y de que seguimos pensando
en pesetas, todos sabemos que 6 euros son 1.000 pesetas, así que
jugando un poco con esta relación, los he situado en forma de triángulo
y os propondré un problema geométrico:
Calculad
el área que queda en medio de los 6 euros, de color granate, teniendo
en cuenta que cada euro tiene un radio, por ejemplo, de un centímetro.
(solución)

LA ESTELLA DE OCHO
PUNTAS
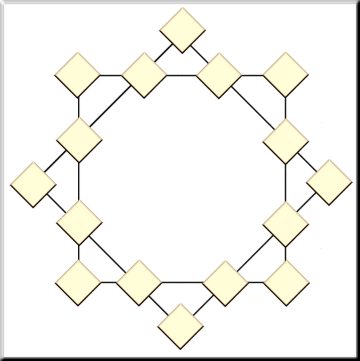
En este problema os propongo completar esta estella de
ocho puntas con los números del 1 al 16 de manera que:
· Todas y cada una de las líneas rectas que la delimitan sumen
34.
· El vértice de cada cuadrado
también sumen 34.
¡¡Ánimos y no
acabéis estrellados!!
(solución)

ESCAQUEANDO
Quizás también seáis aficionados al juego del ajedrez
como yo, o al menos, os parece un juego muy interesante y conozcáis
los movimientos de las piezas y las reglas del juego. En cualquier caso,
hay muchos problemas matemáticos que se pueden plantear a partir
del ajedrez. Veamos varios:

· APERTURA NUMÉRICA:
¿Cuántas jugadas posibles
existen en la primera jugada de ajedrez en total, es decir, considerando
todas las jugadas que pueden hacer las blancas primero y las posteriores
respuestas de las negras?
No es un problema extremadamente complicado,
pero si no tenéis bastante con esto, entonces podéis calcular
el número de jugadas de que disponen las blancas en la segunda
jugada, etc.
· LA PIEZA UNIFORME:
¿Cuál es la única pieza del juego del ajedrez que
siempre, es decir, desde cualquier casilla del tablero (si no hay obstáculos)
dispone del mismo número de movimientos o casillas posibles?
· PIEZAS INTOCABLES:
Probablemente conozcáis el problema de las ocho damas, es decir,
situar ocho damas sobre el tablero escaqueado de manera que no puedan amenazarse
o comerse entre ellas (si no lo habéis probado nunca a hacer es,
al menos, entretenido).
Lo mismo podría plantearse con ocho torres, pero en este caso, es
muy sencillo de hallar.
Yo quiero plantear, ahora, una variante con las otras piezas menores, los
alfiles y los caballos.
· ¿Cuántos
alfiles (de casillas blancas y negras a la vez) podemos situar como máximo
en un tablero de ajedrez sin que se coman o se amenacen entre ellos? ¿Cómo?
· ¿Cuántos caballos
podemos situar como máximo en un tablero de ajedrez sin que se coman
o se amenacen entre ellos? ¿Cómo?
· EL REY VIAJERO:
¿De cuántas formas diferentes puede desplazarse el rey blanco desde su casilla
inicial (e1) hasta la posición del rey negro (e8) empleando sólo siete pasos?
(solución)

SOLUCIONES
CRIPTOGRAMA NAVIDEÑO
47
85053
+62847
147947
D = 0, F = 1, O = 2, L = 3, E = 4, A
= 5, B = 6, S = 7, N = 8, T = 9
(No descarto que pueda existir alguna
solución alternativa)
CRIPTOGRAMA MILITAR
93536
- 86753
6783
A = 3, P = 5, R = 6, O = 7, T = 8, C
= 9
(volver)
JEROGLÍFICOS MATEMÁTICOS
1. "Menjo
nous" < -1: menys u 999: nous >
2. "Más
entretenidos" < más (+) entre ten (10)
y dos (2) >
3. "Sense
tanta potència" < 170: cent setanta
an: potència >
4. "Dos mestres,
Teresa i Siset" < 2 + 3: dos mestres
3a: Teresa 6 7: Siset >
5. "Ho sento
Emili per dossis més grans et deus limitar més i menjar bé"
< 1: Ho
(u) 101: sento (cent-u) e1000: emil i·2: i per
dos 6>7: sis major set
101010:
deus lim(a + i - ab: limit a més (limitar més)
i menys ab (menjar bé) >
(volver)
LOS GEMELOS
La pregunta
que nos llevaría al éxito, o sea, a escapar de esta habitación
es:
"¿Cuál
dirías tú que es la puerta que tu hermano me indicará
para salir?"
Si lo analizáis
tranquilamente veréis que los operadores lógicos V (verdadero)
y F (falso), funcionan como los signos matemáticos + (más)
y - (menos), de manera que al igual que estos:
+ ·
- = - o bien - · + = - (positivo
por negativo igual a negativo, o al revés)
V ·
F = F F · V = F (verdadero por
falso igual a falso, o al revés)
Entonces
a cualquier respuesta que nos dé el hermano inquirido sabremos que
la puerta de escape es, justamente, la contraria.
El que dice
la verdad contestará la puerta mala, porque sabe la respuesta del
hermano mentiroso y el que miente también contestará la puerta
mala porque, sabiendo que el hermano sincero diría la puerta buena,
él responde mintiendo sobre esto.
(volver)
ALICIA PER SECULA
Alicia está
contando en bases numéricas variables, así:
4 ·
5 = 12 en base 18
4 ·
6 = 13 en base 21
es decir,
va saltando las bases de tres en tres y si seguimos esta lógica
encontraremos que
¡¡no
puede llegar a 20 como ella se temía!!
Veámoslo:
4 ·
7 = 14 en base 24
4 ·
8 = 15 en base 27
4 ·
9 = 16 en base 30
4 ·
10 = 17 en base 33
4 ·
11 = 18 en base 36
4 ·
12 = 19 en base 39
Pero llegado
este punto podríamos pensar que el siguiente término es:
4 ·
13 = 20 en base 42
cosa que
no es correcta, dado que
4 ·
13 = 20 en base 26
lo cual
rompe la serie lógica comenzada por Alicia!
¡Quizás
a partir de este momento leeréis con más cuidado los cuentos
infantiles!
(volver)
LOS HEXÁGONOS
La relación
entre las dos áreas es 3, es decir,
el área
del hexágono pequeño es un tercio del área del hexágono
exterior.
(volver)
LA LÚNULA
El área
de la lúnula es igual a la del triángulo rectángulo.
En esta
figura podemos distinguir tres elementos:
El triángulo,
que tiene un área 1 / 2
El sector
circular de 90º que envuelve el triángulo y que tiene un área
de PI / 4
El semicírculo
exterior al triángulo que tiene un diámetro que mide V2 /
2
y, por tanto,
tiene un área de : [PI · (V2 / 2)2] / 2 =
PI
/ 4
La lúnula
es igual al triángulo más el semicírculo menos el
sector:
1 / 2
+ PI / 4 - PI / 4 = 1 / 2
(volver)
-
LA ECUACIÓN IMPOSIBLE
Los cuatro
primeros números que resuelven la ecuación de segundo grado
son:
x²
+ y² = z² + w² = N
1²
+ 8² = 4² + 7² = 65 >
(1 + 64 = 16 + 49)
13
+ 123 = 93
+ 103 = 1729
74 + 2394
= 1574 + 2274 =
3262811042
-
Si lo
deseáis os podéis descargar el
programa de cálculo que resuelve esta ecuación para las diversas potencias
creado por Antonio López Vivar:
Calculador
(volver)
OPERACIONES INVEROSÍMILES
El resultado
de la primera es 1
El resultado
de la segunda es 4
(volver)
HEXÁMEROS
50 + 4 +
1 = 55; 55 x 8 = 440; 25 x 3 = 75; 440 + 75 = 515
50 x 7 =
350; 350 + 7 + 1 = 358; 358 x 3 = 1074; 1074 - 100 = 974
(volver)
ARCO OJIVAL
Caben 8 rosetas,
es decir, el área de la roseta es
la octava
parte del área del círculo generador del arco ojival.
(volver)
LOS SEIS EUROS
-
-
Si se dibuja el triángulo que une los seis
centros de las monedas veremos que se forma un triángulo de lado igual a 4 cm:
-
· El área del triángulo es 4·V3, dado
que la base es 4 y la altura 2·V3 (V3
es la raíz cuadrada de 3)
· El área de los círculos (monedas) que quedan dentro de este
triángulo es 2·PI, dado que está compuesta de tres mitades de moneda más
otras tres sextas partes: 3 PI / 2 + 3 PI / 6 = 2 PI
-
Entonces sólo hay que restar estas dos
superficies para obtener el área buscada:
Área intersticial total =
4·V3 - 2·PI
-
-
-
(volver)
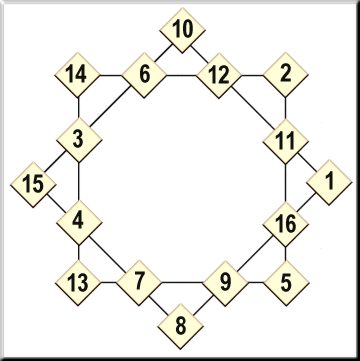
(volver)
ESCAQUEJANDO
> Hay 400
jugadas posibles, 20 de las blancas y 20 de las negras
En la apertura
sólo podemos mover los ocho peones y los dos caballos y cada uno
dispone de 2 movimientos.
> La torre
siempre dispone de 14 movimientos posibles si no tiene obstáculos.
> Podemos
situar 14 alfiles, 7 blancos y 7 negros.
> Podemos
situar 32 caballos sin que se coman unos a otros.
(volver
a los problemas)

Volver al índice
Autor: Blai Figueras Álvarez

E-mail:
mentaludix@hotmail.com






 No
nos trasladaremos a la Edad Media, pero sí que os plantearé
unas cuestiones en relación a los arcos ojivales:
No
nos trasladaremos a la Edad Media, pero sí que os plantearé
unas cuestiones en relación a los arcos ojivales:
 Ya tenemos el
Ya tenemos el 


