Unidad 5 - Actividad 10

ACTIVIDAD 5.10
EL TEOREMA DE PITÁGORAS REENCONTRADO

Menú inicial
Actividad anterior

Menú de la unidad 5

Si en la actividad anterior hemos demostrado un teorema de Tales utilizando productos escalares, en esta demostraremos el teorema de Pitágoras, en forma directa y en forma inversa, también utilizando productos escalares.

Teorema de Pitágoras en forma directa:
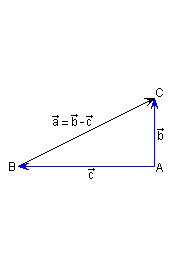
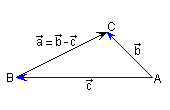
Sea un triángulo ABC rectángulo en A, y sean = 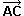y =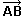, es decir, los catetos (ver la figura). Entonces podemos poner la hipotenusa como la diferencia = -; calculemos su módulo al cuadrado:
||² = |-|² = (-)² =² - 2·+² =²+² = ||²+ ||²
ya que al ser los dos vectores y perpendiculares, su producto escalar es cero. Obtenemos pues que el cuadrado de la hipotenusa es la suma de los cuadrados de los catetos.
Teorema de Pitágoras en forma inversa:
Sea un triángulo ABC que verifica ||² = ||²+ ||², (siendo=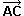, = 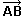y ==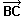-). Entonces, puesto que se verifica siempre
||² = |-|² = (-)² =² - 2·+² = ||² - 2·+ ||²
ha de ser necesariamente 2·, por tanto ·= 0, los dos vectores y son perpendiculares, y el triángulo ABC es rectángulo con ángulo recto en A.

ACTIVIDAD INTERACTIVA

Este applet pone de manifiesto que si dos vectores y son perpendiculares (es decir, ·= 0) entonces entre ||,
|| y |-| se verifica la relación:
|-|² = ||²+ ||²(que llamaremos relación de Pitágoras) y recíprocamente.

¿Cuáles de las siguientes parejas de vectores y verifican la relación de Pitágoras |-|² = ||²+ ||² ?

1)=(2,5) y=(7,-3)
2)=(-2,5) y =(10,4)
3)=(2,4) y =(6,-2)
4)=(6,9) y =(3,-2)

PROPUESTA DE TRABAJO

(¿Quieres un documento Word preparado para hacer este trabajo?)

Demuestra el teorema del coseno a² = b²+c²-2bcCosA utilizando productos escalares.
Indicación: con la misma notación utilizada en el teorema de Pitágoras (es decir,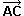

=

,

=

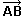y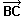

=

=

-

), calcula |

|² = |

-

|² , y ten en cuenta que en un triángulo cualquiera,

·

no es cero.

FIN DE LA ACTIVIDAD 5.10
EL TEOREMA DE PITÁGORAS REENCONTRADO

Menú inicial
Actividad anterior

Menú de la unidad 5