ACTIVITY 1.3
COMMUTATIVITY OF THE ADDITION - THE PARALLELOGRAM LAW

To add two vectorsandinstead of placingafter we placeafter, look at the bottom part of the figure of the right, we observe that the result is the same vector.

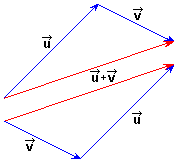
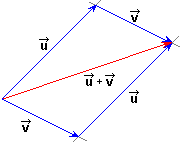
This construction states that the vector addition is commutative:

+ =+

This commutative property allows to make the vector addition using the called
PARALLELOGRAM LAW:

1) We draw the two vectorsand with the same origin

2) We complete one parallelogram tracing:
   - A segment parallel to the vectorby the end of the vector
   - A segment parallel to the vectorby the end of the vector

3) The sum+of the two vectors and is the orientated diagonal of the parallelogram obtained (the origin of + is the common origin of and).

INTERACTIVE ACTIVITY

You have two vectorsandand his vector addition obtained applying the parallelogram law.

You can move the ends A and B of the vectors.

Move the points A and B, and notice the behaviour of the addition of two vectors.
For example, observe what succeeds when the two vectors form one obtuse angle.

Can you manage with the parallelogram law the sum equal to null vector?

SOLUTION

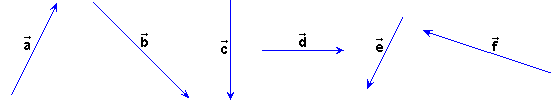END OF ACTIVITY 1.3
COMMUTATIVITY OF THE ADDITION - THE PARALLELOGRAM LAW