|
ACTIVITY 4.4 |
|||
The barycenter or centroid G of a triangle ABC is the point of intersection of the medians AP, BQ and CR; and one median of a triangle is the segment that it has by extremes a vertex and the midpoint of the opposite side. The vectors let us calculate the coordinates of the barycenter of a triangle, knowing coordinates of its vertexes. We use the next property of the barycenter: two segments which barycenter divides each median are in relation 2 is to 1. In other words, on each median the barycenter is located in 2/3 of the vertex and to 1/3 of the opposite side. This quality can be expressed of many ways, using vectors; for instance,  or else  , where P is the midpoint of the side BC.
|
|
If we get G applying to the point A a translation of vector If A(a1,a2), B(b1,b2) and C(c1,c2), this last result said to us that the coordinates of the barycenter G of the triangle ABC are:
|
 |
, we can establish next chain of equalities:
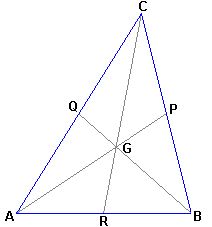INTERACTIVE ACTIVITY Calculate the barycenter G of next triangles ABC. Check the result in the applet of the right side later.
|
| HOMEWORK |
a) That always takes place |
+
+
=
.
+
+
= 3
.END OF ACTIVITY 4.4 |
|||