| 1.0.4.2.
Sistemes de numeració. |
|
Però
el camí ha estat llarg i els ordinadors internament continuen
treballant de la mateixa manera. Més ràpids i en processos
més complicats, però bàsicament treballen igual que els pioners.
Un microprocessador no més pot entendre una sèrie de
polsos elèctrics. Hi ha tensió o no hi ha tensió.
Passa corrent o no passa. |
|
| Van
estar els treballs de Von Neuman
i l’aplicació de l’àlgebra de Boole – George
Boole, lògic i matemàtic britànic 1815-1846 - les que
en un inici van possibilitar el que tenim avui en dia.
Von
Neumann, va definir la idea de màquina universal.
Aquesta resoldria qualsevol aplicació
interpretant una sèrie de instruccions elementals
simples però ordenades i combinades en un programa
que ha de permetre solucionar qualsevol algoritme.
L’àlgebra
booleana representa relacions lògiques
mitjançant l’anotació algebraica de les funcions bàsiques
suma, resta i negació o complementació. |
 |
| Per
què? Doncs, per què el seu pas a un llenguatge què entengués
una màquina elèctrica era molt fàcil i com no lògic!
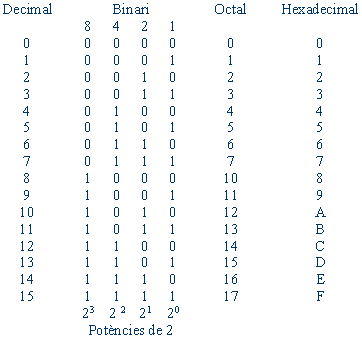
Un
sistema de numeració és un conjunt de símbols
i regles matemàtiques que fem servir per representar dades
numèriques o xifres.
El
més utilitzat és el sistema decimal o base 10.
En diem decimal o base 10, per que 10 són els
símbols utilitzat per representat quantitats ( del 0 al 9).
Tot número decimal es pot descomposar en potencies de deu. |
Així
que els estats elèctrics de funcionament dels
primers ordinadors varen ésser substituïts pels famosos estats
lògics “0” i “1” o “low” i “high”. |
| Exemple
1:
Descomponeu
el número 425,25 en potencies de deu.
425’25
= 400 + 20 + 5 + 0,2 + 0,05 = 4 · 100 + 2 · 10 + 5 · 1 + 2
· 1/10 + 5 · 1/100
425’25
= 4 · 102 + 2 · 101 + 5 · 100
+ 2 · 10-1 + 5 · 10-2
D’aquest
exemple obtindrem el polinomi general que defineix el sistema
numèric decimal:
N10)
= a n · 10 n + a n-1 · 10
n-1 + …+ a 1 · 10 1 + a 0
· 10 0 + a -1 · 10 –1 +…+
a -(n-1) · 10 -(n-1) + a -n
· 10 -n
on:
N
10) = número d’un sistema ( com aquí és el 10,
sistema decimal).
a
= xifra o símbol numèric ( segons número amb el que treballem).
10
= Base sistema numèric ( aquí es el decimal).
n
= Posició que ocupa la xifra ( ordenades segons posició, des
de la coma a esquerra positius, negatius a la dreta) (També
es denomina pes).
Per
utilitzar aquest polinomi amb altres sistemes numèrics només
caldrà substituir la base.
El
sistema de numeració binari és un sistema que només
utilitza dos símbols el 0 i l’1, per això també es denomina
base dos. Aquest sistema és idoni per sintetitzar la informació
i per això serà l’utilitzat per l’anàlisi i el disseny dels
circuits digitals. |
|
 |
Però
hi ha altres sistemes de numeració útils pel tractament de
la informació digital, aquests són el: |
Sistema
Octal.
Sistema
amb buit dígits, també es diu de base 8.
Sistema
Hexadecimal.
Sistema
amb els deu dígits del decimal i les cinc primeres lletres
de l’abecedari, també es diu de base 16.
Donat
que aquests son sistemes àmpliament utilitzat caldrà conèixer
com fer la Conversió entre sistemes numèrics:
Per
convertir un número a decimal, des de qualsevol altre
sistema utilitzarem, el polinomi general
amb la base del sistema origen. |
|
| Exemple
2:
Quin
número decimal és el número binari 1001.
1001
en base dos = 1·23 + 0·22 + 0·21
+ 1·20 = 8+0+0+1 =9
Per
passar del sistema decimal a qualsevol altre sistema dividirem
successivament aquest per la base del sistema al qual volem
convertir. |
|
| Exemple
3:
Quin
número binari és el 32 en base deu?
32:2=16
i la resta és 0
16:2=8
i la resta és 0
8:2=4
i la resta és 0
4:2=2
i la resta és 0
2:2=1
i la resta és 0
Agafarem
l’últim quocient ( que serà la xifra més significativa) i
les restes successives i obtimdrem el número en base dos
100000
Per
passar de binari a octal o hexadecimal i al inreves, Veiem
uns exemples clarificadors. |
|
| Exemple
4:
Passeu
el següent número binari 1110001 al sistema octal.
El
primer que fareu és agrupar en blocs de 3 xifres, a partir
de la de menys pes el número binari.
1
110 001
Desprès
el donareu el valor en el sistema octal.
1=1
110=6 001=1
i
ja tindreu el número en base 8.
161
en base 8 |
|
| Exemple
5:
Passeu
el número 67 en base 8 a base dos.
Aquí
actuarem de manera inversa:
6=110
7=111
El
resultat és:
110111
en binari |
|
| Exemple
6:
Passeu
el següent número binari 11110001 al sistema hexadecimal.
El
primer que fareu és agrupar en blocs de4 xifres, a partir
de la de menys pes el número binari.
1111
0001
Desprès
el donareu el valor en el sistema octal.
1111=F
001=1
i
ja tindreu el número en base 16.
F1
en base 8 |
|
| Exemple
7:
Passeu
el número A32 hexadecimal al sistema binari
Aquí
actuarem de manera inversa:
A=1010
3=0011 2=0010
El
resultat és:
101000110010
en binari |
|
Activitats
Feu
les següents conversions de sistema numèric:
1.
El número 14 en base deu al sistema binari. r.1110
2.
El número decimal 37 a base dos. r.100101
3.
El número binari 1110 , 1001 al sistema decimal. r. 14,56
4.
El número binari 1110 a base 8. r.16
5.
El número en base 2 100101 a base 8. r.45
6.
El número octal 16 al sistema decimal. r.14
7.
El número octal 45 a base deu. r.37
8.
El número decimal 110 a hexadecimal. r.6E
9.
El número 25 hexadecimal a decimal. r.37
10.
El número 25,86 decimal a hexadecimal. r. 19,DC2 |
|
| Així
doncs l’àlgebra de Boole té com objectiu
definir una sèrie de símbols per representar objectes o fenòmens
que donin lloc a expressions matemàtiques més complexes anomenades
funcions., Aquestes funcions, com veurem
més endavant, no operem amb relacions quantitatives,
sinó que ho fa amb relacions lògiques.
Entendrem
com funció lògica aquella que tindrà “n”
variables (representades per lletres), les quals no
més podran tenir dos valors, i que estaran relacionades
per les operacions bàsiques : suma, producte.
Veiem
per exemple la següent funció:
F
= a·b·c+a·b
D’ella
podriem dir:
Que
es pot representar de forma genèrica: F = f (a,b,c)
Que
llegirien com: F és una funció de a, b i c.
La
funció o variable depenent és la F.
Les
variables binaries son a, b i c.
Les
operacions son la suma i el producte.
L’expressió
algebraica es llegiria així: La funció lògica serà 1 quan
el producte de a, b i c o a per b siguin 1.
Els
valors lògics de les variables seran:
0
= 0 lògic o nivell baix de tensió o absència de tensió.
1
= 1 lògic o nivell alt de tensió o presència de tensió.
Si
bé un senyal digital es representa per un valor lògic, en
realitat correspon a una franja de tensió, així direm per
exemple que l’1 lògic serà el valor de tensió compres entre
7 i 10 volts i 0 lògic entre 0 i 3 volts. La zona intermitja
es denomina prohibida ja que el valor lògic queda indeterminat.
Operacions
i propietats bàsiques de l’àlgebra de Boole.
En
aquest tipus d’àlgebra tindrem tres operacions bàsiques:
la suma, el producte i la complementació o inversió que també
denominarem negació.
La
següent taula ens mostra la forma de representar-la i els
seus postulats bàsics |
Funcions
lògiques o boleanes.
Funcions
lògiques o boleanes. A més del sistema numèric binari,
caldrà un nou component que ens permeti relacionar i operar
amb aquest sistema, per tal de poder operar en el complex
mon del disseny i la síntesi dels sistemes electrònics digitals.
Això ens ho permet l’àlgebra de Boole. |
|
Operació |
Representació |
Postulats
bàsics |
|
Suma |
F
= a + b |
0+0=0
0+1=1
1+1=1 |
a+0=a
a+1=1 |
a+a=a
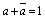
|
|
Producte |
F
= a · b |
0·0=0
0·1=0
1·1=1 |
a·0=0
a·1=a |
a·a=a
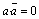
|
|
Inversió,
Complementació o negació |
F
= 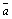
F
= 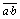
|
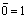
|
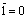
|
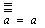
|
|
|
| Encara
que existeixen nombrosos teoremes, hi ha 10 que es necessari
conèixer donada la seva extrema utilitat. D’aquest 10 també
coneixerem la seva forma dual. Que és una forma dual? Doncs
aquella expressió en la que canviant les operacions suma per
producte i producte per suma, defineixen altre teorema. Veieu-les
a continuació: |
Teoremes
i lleis principals de l’àlgebra de Boole. |
| Lleis |
Forma
bàsica |
Forma
dual |
| Commutativa |
a+b=b+a |
a·b=b·a |
| Associativa |
a+(b+c)=(a+b)+c=a+b+c |
a·(b·c)=(a·b)·c=a·b·c |
| Distributiva |
a+(b·c)=(a+b)·(a+c) |
a·(b+c)=(a·b)+(a·c) |
| Element
neutre |
a+0=a |
a·1=a |
| d’absorció |
a+a·b=a |
a·(a+b)=a |
| Teorema
de De Morgan |
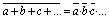
|
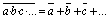
|
| de
transposició |
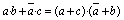
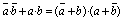
|
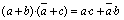
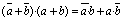
|
| altres
lleis |
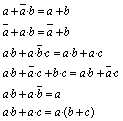
|
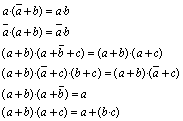
|
|
|
|
by
Jordi Jordan |