|
El límit d'una funció és un concepte fonamental de les matemàtiques. N'hi han de dos tipus, `lim_{x\to \infty} f(x)`, límits quan la `x` tendeix a `\infty` i `lim_{x\to a}f(x)`, límits quan `x` tendeix a un número concret. El segon cas, `lim_{x\to a}f(x)`, és per estudiar que li passa a una funció en un lloc concret. El primer cas, `lim_{x\to \infty} f(x)` és per saber que li passa a la funció, a la llarga. L'estudi d'quests tipus de límits són molt semblants als límits de successions que acabem de fer. Per la qual cosa començarem a estudiar primer aquests. Tot i així començarem amb un exemple que ens ajudarà a començar a descobrir el tema. A finals del segle XVII el genis més gran de la humanitat, segons molta gent que en sap, Sir Isaac Newton, va descobrir una senzilla fórmula que describia el moviment de tots els astres de l'univers. Aquesta fórmula és el que coneixem com llei de la gravetat que deia, totes les coses de l'univers, per exemple la Terra i la Lluna, el Sol i el sistema Terra-Lluna, entre nosaltres mateixos,... exercim una força atractiva entre nosaltres que és proporcional al producte de ls nostre masses (o sigui si la massa és més gran la força també) i inversament proporcional al quadrat de la distància (o sigui que quan més lluny, menys força). La funció, `f(x)`, que descriu aquesta força en funció (valga la redundància) de la distància, `x`, és:  On `M` i `m` són les masses dels dos cossos i `G` una constant, que en diem constant de la gravitació universal que depèn de les unitats que fem servir per mesurar les masses (SI, `kg`) i les distàncies (SI, `metres`). `G=6'64·10^(-11)(N·m^2)/(kg^2)`. Però pel que volem fer això no té massa importància. En té molta d'importància, però aquí, no és trascendent. El que nosaltres volem contestar és a la pregunta de quant val la força si els dos cossos estan cada vegada més lluny?. Fixeu-vos que el que hi ha a dalt, és una constant, per la qual cosa tenin en compta que, `G·M·m=C` `f(x)=C/x^2`. Si en lloc de posar `x` posem, `n`, podem veure això com en el tema anterior, `a_n=C/n^2`, i preguntar-nos sobre quan val la força quan la distància és cada vegada més gran serà el mateix que preguntar-nos pel: `lim C/n^2=0`, ja que tenim el quocient de dos polinomis en que el grau de baix és més gran que el de dalt. Però nosaltres no tenim una succesió, tenim una funció, `f(x)=C/x^2`, per calcular el límit ho podrem fer igual que quan ho feiem amb les successions, però caldrà tenir en compte dues grans diferències. 1-`n`, agafava valors naturals, `{1,2,3,4,...}`. En canvi `x`, pot agafar qualsevol valor real, vol dir que entre l'`1` i el `2` hi ha un continu d'enfinits nombres. 2-I la `x` ara a part d'anar cap a `+\infty` també pot anar cap a `-\infty`. Per la qual cosa si nosltres volem saber quan val la força de la gravetat entre dos cosos a mesura que la distància entre ells és més gran haurem de calcular. Que evidentment tendeix a `0` ja que el grau del polinomi de dalt és més gran que el de baix. Però també ens podem preguntar cap on tendeix la força a mesura que els dos cosos s'acosten. És a dir quan la distància entre els dos cossos tendeix a `0`. Aquí introduïm el nou concepte, que no era a les successions, límit d'una funció quan `x` tendeix a un número, lim_{x\to a}f(x)`. En el nostre cas: Que val, `+\infty`. Es deixa al lector explicar per què, ja que això serà el el motiu del tema següent. Tot i així aquest estrany, `+\infty` que a la gent no li sembli estrany, és la causa de la existència dels forats negres i de que a la peli, Apolo XIII, cap al final en Tom Hanks (que encarnava a l'autèntic astronauta, James Lovell) digués, la Terra cada vegada es veu més grossa.  Per cert, ja que hem parlat de forats negres, algú podria pensar que, per què no ens colapsem nosaltres mateixos?, ja que cadascun dels nostres àtoms exerceix una força gravitatòria atractiva envers els altres. La resposta a aquesta pregunta involucra a una altra força fonamental, la força elèctrica, que com sabeu, pot ser repulsiva. Però ho deixarem aquí, que si no marxem massa del tema ;-). Tornem als límits a l'`\infty`. Acabem de veure que n'hi ha de dos tipus, cap a `+\infty` i capa `-\infty`. Veiem exemples senzills. `lim_{x\to +\infty}(3x^3)/(2x^2-5x)` tenim un quoceint de dos polinomis en que el grau de dalt és més gran que el de baix per la qual cosa s'en va a `\infty` i el signe deprendrà des coefients, com tots dos són positius, Però què passaria si en lloc d'anar a `+\infty` el límit fos a `-\infty`. `lim_{x\to -\infty}(3x^3)/(2x^2-5x)`, llavors no només hem de mirar els signes dels coeficients, sinó que també hem de mirar el signes hi posen les `x`. Així: 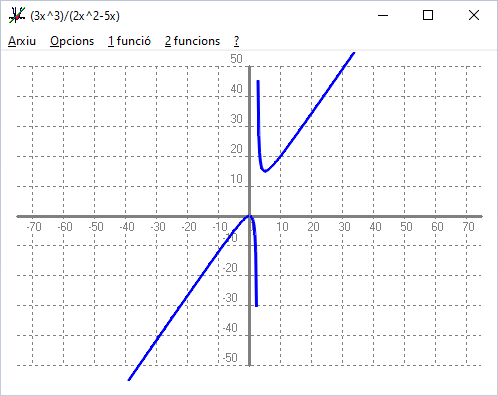 A continuació el que cal és fer exercicis al respecte: |