|
Notes a les solucions:
1-Siguin $$ A=\begin{pmatrix} 2&1\\\ 3&2 \end{pmatrix}, B=\begin{pmatrix} 2&-1\\\ -3&2 \end{pmatrix} $$ i la matriu identitat d'ordre dos $$ I=\begin{pmatrix} 1&0\\\ 0&1 \end{pmatrix} $$ a) Comproveu que `(A-2I)^2=3I` [0,5 punts] Solució:
A-2I=\begin{pmatrix} 2&1\\\ 3&2 \end{pmatrix}- 2\begin{pmatrix} 1&0\\\ 0&1 \end{pmatrix}= \begin{pmatrix} 2&1\\\ 3&2 \end{pmatrix}+ \begin{pmatrix} -2&0\\\ 0&-2 \end{pmatrix}= \begin{pmatrix} 0&1\\\ 3&0 \end{pmatrix} $$ $$ (A-2I)^2=\begin{pmatrix} 0&1\\\ 3&0 \end{pmatrix}· \begin{pmatrix} 0&1\\\ 3&0 \end{pmatrix}= \begin{pmatrix} 3&0\\\ 0&3 \end{pmatrix}=3I $$ b) Utilitzant la igualtat de l’apartat anterior, trobeu la matriu inversa de la matriu `A` en funció de les matrius `A` i `I`, i comproveu que coincideix amb la matriu `B`. [1,25 punts] Solució:
`(A-2I)·(A-2I)=3I` `A^2-2IA-A2I+2I2I=3I` `A^2-4A+4I=3I` `A^2-4A=3I-4I` `A^2-4A=-I` `4A-A^2=I` `(4I-A)A=I` `A^(-1)=4I-A` $$ 4I-A=\begin{pmatrix} 4&0\\\ 0&4 \end{pmatrix} -\begin{pmatrix} 2&1\\\ 3&2 \end{pmatrix}= \begin{pmatrix} 2&-1\\\ -3&2 \end{pmatrix} $$ c) Calculeu la matriu `X` que satisfà la igualtat `A · X = B`. [0,75 punts] Solució:
`A^(-1)·A·X=A^(-1)·B` `X=A^(-1)·B` `X=B·B` $$ X=B^2=\begin{pmatrix} 2&-1\\\ -3&2 \end{pmatrix}· \begin{pmatrix} 2&-1\\\ -3&2 \end{pmatrix}= \begin{pmatrix} 7&-4\\\ -12&7 \end{pmatrix} $$ 2-Sigui la funció `f(x)=1/x`. a) Calculeu l’equació de la recta tangent a la gràfica de la funció `f` en el punt d’abscissa `x = 2`. [0,75 punts] Solució:
`f'(x)=-1/x^2` que en el punt `f'(2)=-1/4` Per trobar l'equació de la recta tangent ho podem fer amb la punt pendent, `y-y_0=m(x-x_0)` `y-1/2=-x/4+1/2` `y=-x/4+1/2+1/2` `y=-x/4+1` ANNEX:
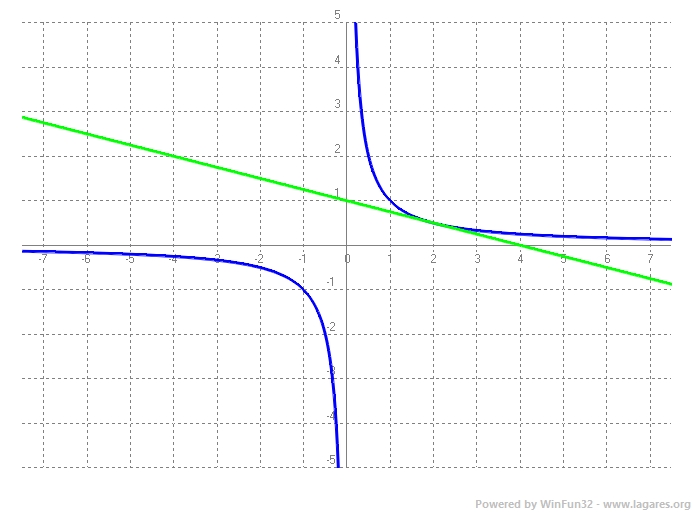 b) Calculeu l’equació de la recta tangent a la gràfica de la funció `f` en el punt d’abscissa `x = k`, en què `k` és un nombre real positiu. [0,75 punts] Solució:
L'equació punt pendent serà: Si ho volem expressar amb l'equació explícita, com abans: `y=-x/k^2+1/k+1/k` `y=-x/k^2+2/k` c) Comproveu que, tal com es pot veure en la figura de sota, la recta de l’apartat `b` determina un triangle d’àrea constant amb els semieixos positius de coordenades. Calculeu aquesta àrea. [1 punt] 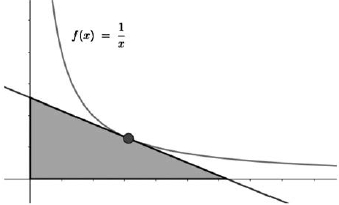 Solució:
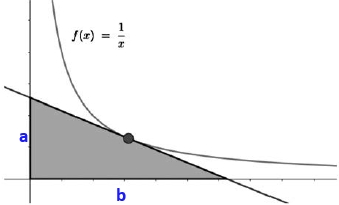 Per trobar `a` cal trobar la imatge de `x=0 => a=-0/k^2+2/k=2/k` Per trobar, `b` cal trobar el punt de tall amb l'eix de les `x => y=0 =>`
`x/k^2=2/k` `x=2k^2/k` `x=2k => b=2k` Finalment per trobar l'àrea del triangle només cal multiplicar la base · l'altura i dividir-ho per `2`. I comprovem que no depèn del punt `k` triat. 3-Sigui el sistema d’equacions lineals , en què `m` és un nombre real. $$ \begin{cases} 2x+y=1+z\\ my+z=2-x\\ mz+3=3x+y \end{cases} $$ a) Discutiu el sistema segons els valors del paràmetre `m`. [1,25 punts] Solució:
$$ \begin{cases} 2x+y-z=1\\ x+my+z=2\\ -3x-y+mz=-3 \end{cases} $$ $$ M=\begin{pmatrix} 2&1&-1\\\ 1&m&1\\\ -3&-1&m \end{pmatrix} $$ $$ Det(M)=\begin{vmatrix} 2&1&-1\\\ 1&m&1\\\ -3&-1&m \end{vmatrix}= 2m^2-3+1-(3m+m-2)=2m^2-4m $$ Cal resoldre aquesta equació: `2m^2-4m=0` `2m(m-2)` Que té dues solucions `m=0` i `m=2` b) Resoleu el sistema, si té solució, per al cas `m = 1`. [1,25 punts] Solució:
$$ \begin{cases} 2x+y-z=1\\ x+y+z=2\\ -3x-y+z=-3 \end{cases} $$ $$ \begin{cases} x+y+z=2\\ 2x+y-z=1\\ -3x-y+z=-3 \end{cases} $$ $$ \begin{cases} x+y+z=2\\ -y-3z=-3\\ 2y+4z=3 \end{cases} $$ $$ \begin{cases} x+y+z=2\\ y+3z=3\\ 2y+4z=3 \end{cases} $$ $$ \begin{cases} x+y+z=2\\ y+3z=3\\ -2z=-3 \end{cases} $$ $$ \begin{cases} x+y+z=2\\ y+3z=3\\ z=3/2 \end{cases} $$ `y+9/2=3` `y=-9/2+3` `y=-3/2` Anem a la primera equació `x+y+z=2`: `x=2` `x=2, y=-3/2, z=3/2` 4-Sigui la funció `f(x)` definida per `f(x) = –3x + e^(2x^(3)-1)`. a) Justifiqueu que `f(x) = 2` té una solució en l’interval `(–1, 0)`. [1,25 punts] Solució:
Anem a veure quins valors agafa aquesta funció en els extrems de l'interval:
`g(0)=-3·0+e^(-1)=e^(-1)>0` Com `g(x)` és una funció contínua (ja que és suma de funcions contínues) i en els extrems d'un interval la funció agafa signes diferents, pel teorema de Bolzano, en aquest interval la funció ha de tenir, com a mínim, un `0 => f(x)=2` té com a mínim una solució. b) Sigui la funció `h(x) = –3x^2 + e^(2x^(3)–1)`. Calculeu l’àrea de la regió compresa entre les gràfiques de les funcions `f(x)` i `h(x)`. [1,25 punts] Solució:
`-3x=-3x^2` `3x^2-3x=0` `3x(x-1)=0` Dues solucions `x=0` i `x=1` Per trobar l'àrea compresa entre les dues funcions cal trobar la integral definida entre els dos punts de tall de la funció diferència de les dues funcions. Si el resultat ens dona negatiu vol dir que hem restat l'inferior menys la superior i cal dir que l'àrea és el valor absolut.
Àrea `=|\int_0^1 (3x^2-3x) dx| = |[x^3-3/2x^2]_0^1| = |1^3-3/2·1^2-0| = |1-3/2|= |-1/2|=1/2 u^2` ANNEX:
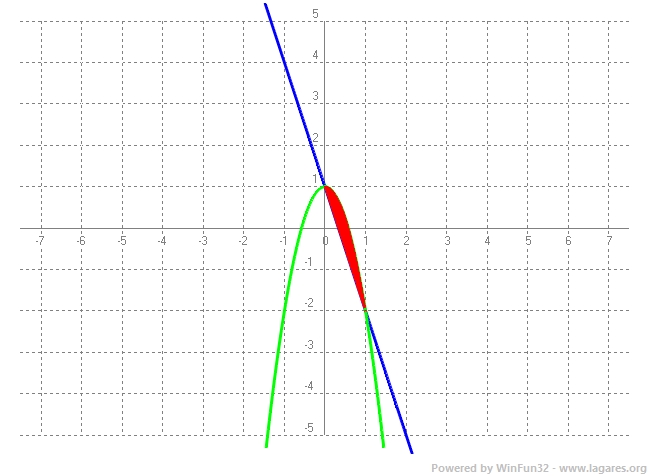 5-Siguin `r_1` i `r_2` les rectes definides per `r_1: x – 1 = y = –z` i per `r_2: x = y = z`, respectivament. a) Calculeu l’equació paramètrica de la recta que talla perpendicularment les rectes `r_1` i `r_2`. [1,75 punts] Solució:
`r_1: (x,y,z)=(1,0,0)+(1,1,-1)lambda =(1+lambda, lambda, -lambda)`
`r_2: (x,y,z)=(0,0,0)+(1,1,1)mu=(mu,mu,mu)` Nosaltres cerquem un vector que vagi d'un punt d'una recta aun punt de l'altra i sigui perpendicular a cadascun dels vectors directors.
Fem el producte escalar amb cadascun dels vectors directors i el resultat ha de donar `0`.
`(mu-lambda-1,mu-lambda, mu+lambda)·(1,1,1)=mu-lambda-1+mu-lambda+mu+lambda=3mu-lambda-1=0` Que defineix un sistema amb que trobarem, `lambda` i `mu`, o sigui els dos punts de cadascuna de les dues rectes- $$ \begin{cases} \mu-3\lambda=1\\ 3\mu-\lambda=1 \end{cases} $$ $$ \begin{cases} -3\mu+9\lambda=-3\\ 3\mu-\lambda=1 \end{cases} $$ $$ \begin{cases} \mu-3\lambda=1\\ -9\mu+3\lambda=-3 \end{cases} $$ `P=(mu,mu,mu)=(1/4,1/4,1/4)` i `Q=(1+lambda, lambda,-lambda)=(1-1/4,-1/4,1/4)=(3/4,-1/4,1/4)` O sigui, el vector, `\vec{PQ}=(1/4,1/4,1/4)-(3/4,-1/4,1/4)=(-2/4,2/4,0)=(-1/2,1/2,0)` La recta que passi per qualsevol dels dos punts, `P` o `Q` i tingui com a vector director aquest vector `\vec{PQ}` passarà per ambdues rectes i en serà perpendicular a totes dues.. Per la qual cosa l'equació d ela recta demanada pot ser la que passa per `P` i té com a vector director `\vec{PQ}`. ANNEX:
`(x,y,z)=(1/4,1/4,1/4)+nu(-1,1,0)=(1/4-nu,1/4+nu,1/4)` b) Calculeu la distància entre `r_1` i `r_2`. [0,75 punts] Solució:
6-Volem construir una peça metàl·lica que tingui per secció un trapezi isòsceles amb la base superior tres vegades més llarga que la base inferior. Els altres costats del trapezi fan `10` mm, tal com podeu observar en la figura següent: 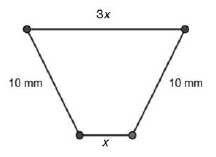 a) Expresseu l’altura del trapezi en funció de la longitud `x` de la base inferior. [0,5 punts] Solució: 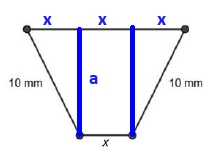 Fixeu-vos que tenim un triangle rectangle que ha de complir el teorema de Pitàgores `a^2+x^2=10^2` b) Calculeu la longitud de la base inferior del trapezi de manera que l’àrea de la peça sigui màxima i trobeu el valor d’aquesta àrea màxima. [2 punts] Solució:
Per trobar el màxim cal trobar quan la derivada val `0`.
`2\sqrt{100-x^2}-(2x^2)/\sqrt{100-x^2}=0` `\sqrt{100-x^2}=x^2/\sqrt{100-x^2}` `100-x^2=x^2` `100=2x^2` `50=x^2` `x=+-\sqrt{50}` Que evidentment la solució negativa no té cap sentit `=> x=\sqrt{50}` L'altura val `a=\sqrt{100-x^2}=\sqrt{100-\sqrt{50}^2}=\sqrt{100-50}=\sqrt{50}` L'àrea demanada és `A=(a·2x)=(\sqrt{50}·2\sqrt{50})=2·50=100` `mm^2` Per demostrar que això és un màxim podem trobar el valor de l'àrea en dos punts, un a l'esquerra i l'altre a la dreta, `x=\sqrt{50} \approx 7,071067`. A l'esquerra `x=0` i a la dreta `x=10`. `A(x)=2x·\sqrt{100-x^2} => A(0)=0·\sqrt{100}=0 i A(10) = 10· \sqrt{100-100}=0` Que evidentment són àrees més petites que la que val `100`. Per la qual cosa en `x=\sqrt{50}` l'àrea té un màxim. |