|
- Si tens un quadrat que mesura un metre de costat, quant val la seva àrea?. Fes una taula que en la primera columna escriguis la mesura del costat del quadrat (en metres) 0, 0'25, 0'5, 1, 2, 3, 4 i en la segona columna hi posis el que mesura la seva àrea (en metres2). A continuació dibuixa una gràfica representant aquests punts. Amb compte, tracta de dibuixar la forma de la gràfica de tota la funció. Sabries dir quina és la fórmula de la funció?  - Si tens un cercle que mesura un metre de radi, quant val la seva àrea?. Fes una taula que en la primera columna escriguis la mesura del radi (en metres) 0, 0'25, 0'5, 1, 2, 3, 4 i en la segona columna hi posis el que mesura la seva àrea (en metres2). A continuació dibuixa una gràfica representant aquests punts. Amb compte, tracta de dibuixar la forma de la gràfica de tota la funció. Sabries dir quina és la fórmula de la funció?.  - De les següents paràboles indica'n, el vèrtex, els punts de tall amb els eixos, si té les "banyes" amunt o avall. a) 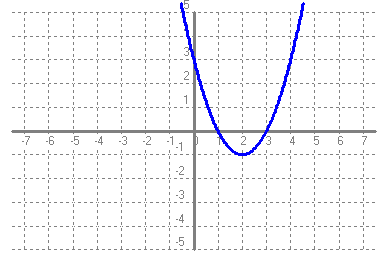 b) 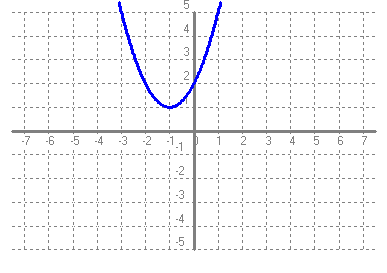 c) 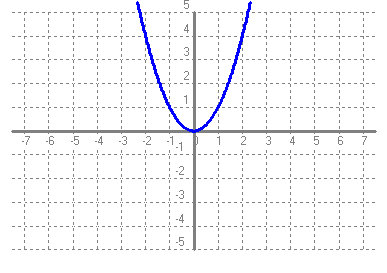 d) 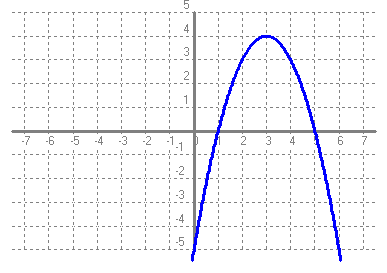 - Dibuixa a partir de la taula de valors les funcions, f(x) = x2, g(x) = 2x2 i h(x) = 1/2x2. Per veure si ho has fet bé pots fer-ho també amb el programa funcions. Pots treure'n alguna conclusió que relacioni la fórmula amb la forma de la gràfica? Suggeriment, pots experimentar dibuixant, amb el programa funcions, funcions de segon grau similars. - Dibuixa amb el programa funcions les funcions de segon grau següents, f(x) = -x2, g(x) = -2x2 i h(x) = -1/2x2. Pots treure'n alguna conclusió que relacioni la fórmula amb la forma de la gràfica? Suggeriment, pots experimentar dibuixant, amb el programa funcions, funcions de segon grau similars. Mirant aquest exercici i l'anterior, què pots dir? - Dibuixa amb el programa funcions les funcions de segon grau següents, f(x) = x2 + 2, g(x) = x2 - 1, h(x) = -x2 + 0'5 i k(x) = 2x2 + 2. Explica com és la gràfica de les funcions de segon grau en funció dels dos coeficients que hem escrit. Suggeriment, pots experimentar dibuixant, amb el programa funcions, funcions de segon grau similars. - Dibuixa amb el programa funcions les funcions de segon grau següents, f(x) = (x - 1)2 , g(x) = (x + 2)2, h(x) = (x + 3)2 i k(x) = 2(x - 1)2. Explica com és la gràfica de les funcions de segon grau en funció dels dos coeficients que hem escrit. Suggeriment, pots experimentar dibuixant, amb el programa funcions, funcions de segon grau similars. - Dibuixa amb el programa funcions les funcions de segon grau següents, f(x) = (x - 1)2 - 2, g(x) = (x + 2)2 + 1, h(x) = (x + 3)2 - 3 i k(x) = 2(x - 1)2 - 2. Explica com és la gràfica de les funcions de segon grau en funció dels tres coeficients que hem escrit. Suggeriment, pots experimentar dibuixant, amb el programa funcions, funcions de segon grau similars. - Dibuixa en dos finestres del programa funcions les funcions de segon grau següents f(x) = (x - 2)2 - 1 i g(x) = x2 - 4x + 3. Explica perquè passa el que veus. - Fent servir el que has après en els exercicis anteriors, series capaç de trobar la fórmula de les funcions de l'exercici 3. - A la llibreta, dibuixa les funcions de segon grau següents a partir de trobar el vèrtex xv = -b/(2a), els punts de tall, el sentit de les banyes i algun altre punt que creguis convenient calcular. a) f(x) = x2 -6x +8 b) g(x) = x2 -2x -3 c) h(x) = x2 +2x +2 d) i(x) = -2x2 -4x -1 e) j(x) = 3x2 - Dibuixa la següent funció definida a trossos: $$ f(x)=\begin{cases} 1 \:\:\: \text{ si } \:\: x<-1\\ \\ x^2 \:\:\: \text{ si } \:\: -1\le x \le2\\ \\ -x+4 \:\:\: \text{ si } \:\: x > 0 \end{cases} $$ - Dibuixa la següent funció definida a trossos: $$ f(x)=\begin{cases} x^2 \:\:\: \text{ si } \:\: x<0\\ \\ -x^2 \:\:\: \text{ si } \:\: x \ge 0 \end{cases} $$ - Dibuixa la següent funció definida a trossos: $$ f(x)=\begin{cases} -x^2+1 \:\:\: \text{ si } \:\: x<-1\\ \\ 2x^2-8x+6 \:\:\: \text{ si } \:\: x \ge -1 \end{cases} $$ - Pots escriure la fórmula de la funció definida a trossos que la seva gràfica és: 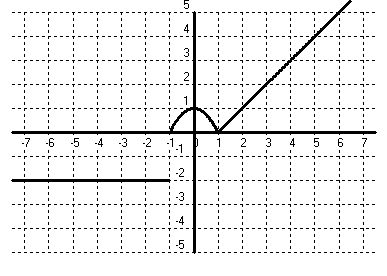 - Galileo va descobrir, al segle XVI, que les coses queien (en el buit) en funció del temps segon la fórmula següent e = 1/2· g · t2. On e és l'espai recorregut, g l'acceleració de la gravetat (val uns 9'8 m/s2, a la pràctica s'agafa 10) i t el temps de caiguda. a) Pots calcular l'espai caigut al cap de 1, 2, 3, 4, 5 segons? b) Dibuixa la gràfica resultant. c) Pots dir que té això a veure amb el que estem estudiant? d) Sabries calcular quant triga un cos que cau a fer 5 metres? e) I a fer-ne 100 de metres? - Si llancem qualsevol cosa cap a dalt, per exemple una pedra o un tret amb una escopeta l'alçada (e d'espai) assolida en funció del temps segueix la següent fórmula, e = -1/2· g · t2 + Vo · t on Vo és la velocitat en que surt el cos disparat. a) Si l'objecte surt a 50 m/s, podries dir quan el cos arribarà al seu punt més alt? Com que la funció que segueix el cos és una funció de segon grau pots fer servir el que has après en els exercicis anteriors sobre el vèrtex. b) Quina altura haurà assolit? c) Quant trigarà a tornar al terra? d) Podries contestar les anteriors tres preguntes en general, ho sigui en funció de la velocitat inicial Vo i de g. - Si tens un cub que fa un dm de costat, quant mesura el seu volum? Fes una taula que en la primera columna escriguis la mesura del costat del cub (en dm) 0'25, 0'5, 1, 2, 3, 4, 5 i en la segona columna hi posis el que mesura volum (en dm3). A continuació dibuixa una gràfica representant aquests punts. Amb compte, tracta de dibuixar la forma de la gràfica de tota la funció. Sabries dir quina és la fórmula de la funció?  - Amb el programa funcions dibuixa la funció f(x) = x3. - Amb el programa funcions dibuixa la funció f(x) = -x3. - Amb el programa funcions dibuixa la funció f(x) = x3 - x. - Amb el programa funcions dibuixa la funció f(x) = x4 i la funció f(x) = x5. - Si una persona triga en pintar un mur 100 dies, a) quant trigarien dues persones? i 4 persones? i 5 persones? i 10 persones? b) Dibuixa una gràfica que relacioni el que es triga a pintar el mur en funció del número de persones que hi treballen. c) Sabries escriure la fórmula de la funció que descriu aquestes dades que han sortit? d) Amb el programa funcions dibuixa la gràfica a partir de la fórmula que has trobat. Segurament hauràs de cambiar l'escala, com a mínim la de l'eix y. e) Hi ha un tros de la gràfica que surt representada que no ens és útil. Quin és? f) Podrien tenir sentit els valors de la gràfica amb x més petits que 1. - Anem per coses més teòriques. Amb el programa funcions dibuixa, 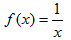 - Amb el programa funcions dibuixa, 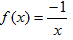 - Amb el programa funcions dibuixa les funcions, 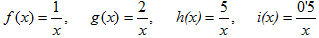 - Amb el programa funcions dibuixa les funcions, 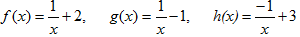 - Amb el programa funcions dibuixa les funcions, 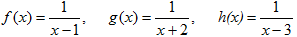 - Amb el programa funcions dibuixa les funcions, 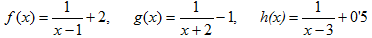 - Sabries dibuixar les funcions dels tres exercicis anteriors en la llibreta sense que suposés massa esforç ni gairebé calcular cap imatge? - Si tens un quadrat que la seva àrea mesura 1 metres2, pots dir quant mesura el seu costat? i si mesura 4 metres2, i si en mesura 9 de metres2. Quin altre valor hauriem de demanar de l'àrea d'un quadrat de manera que també sortís un costat enter? I si l'àrea mesurés 20 metres2, quant mesura el seu costat? Amb els valors trobats pots escriure'n una taula i fer-ne una representació gràfica del valor d'un costat d'un quadrat en funció de la seva àrea? Pots dir-nos quina fórmula descriu aquesta funció? Quin és el seu domini? Quin és el seu recorregut? - Dibuixa amb el programa funcions la funció que acabes de trobar en l'exercici anterior. - Estrictament parlant la funció arrel quadrada no és una funció, perquè? Com ho arreglem per que sigui considerada l'arrel quadrada una funció? - Dibuixa amb el programa funcions: (indica en cada cas el domini i el recorregut) 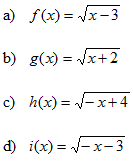 - Si tens un cub que el seu volum mesura 1 metre3, pots dir quant mesura el seu costat? i si mesura 8 metres3, i si en mesura 27 de metres3. Quin altre valor hauriem de demanar al volum d'un cub de manera que també sortís un costat enter? I si el volum mesurés 25 metres3, quant mesura el seu costat? Amb els valors trobats pots escriure'n una taula i fer-ne una representació gràfica del valor d'un costat d'un cub en funció del seu volum? Pots dir-nos quina fórmula descriu aquesta funció? Quin és el seu domini? Quin és el seu recorregut? - Dibuixa amb el programa funcions la funció que acabes de trobar en l'exercici anterior. Resulta que també hi ha gràfica en la part negativa de l'eix de les x, té sentit considerar-ho en el context del problema anterior? Perquè tenen imatges les x negatives? - Dibuixa amb el programa funcions: (indica en cada cas el domini i el recorregut) 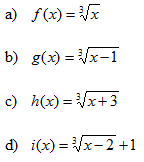 - Digues quina és la fórmula de la funció de cadascuna de les següents gràfiques. a) 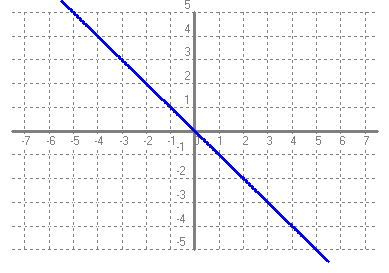 b) 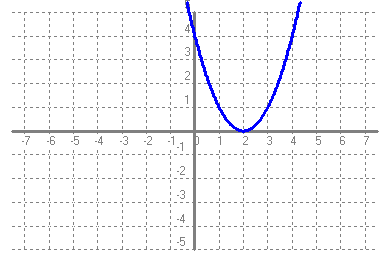 c) 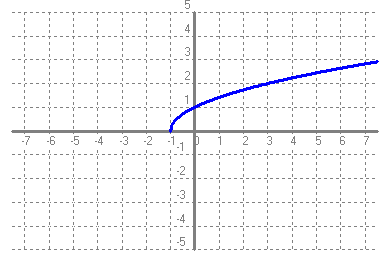 d) 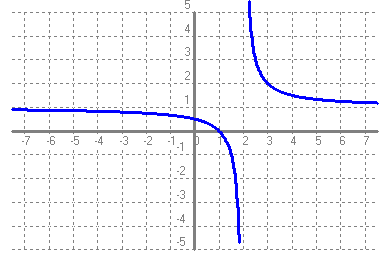 e) 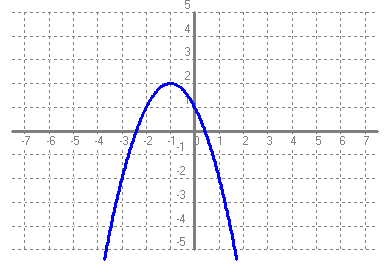 f) 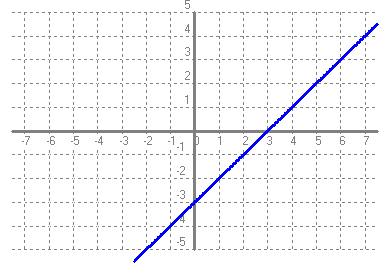 g)  h) 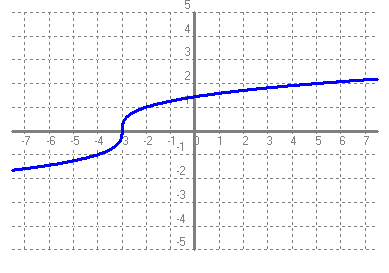 i) 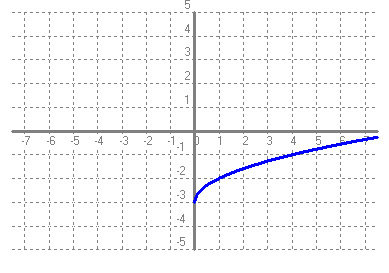 k) 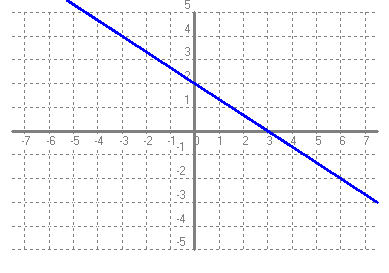 - Sabries dibuixar les següents funcions sense fer taula de valors: 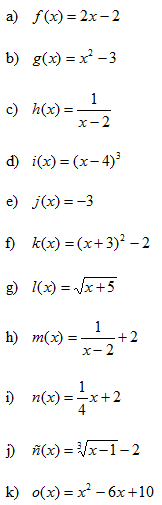 - Amb 200 metres de tanca volem delimitar un recinte rectangular aprofitant una paret molt llarga. a) Construeix la funció que dóna l'àrea a partir de la longitud d'un dels dos costats. b) Digues quin és el domini. c) Quines dimensions ha de tenir la tanca perquè l'àrea engabiada sigui máxima?  - En una habitació sota teulada, que té una paret de forma triangular, hi volem posar un armari. Les mides de l'habitació són 10 metres d'amplada per 4 d'altura en la seva part més alta. Si l'armari té forma rectangular, quina han de ser les seves mides de manera que sigui el més gran possible? 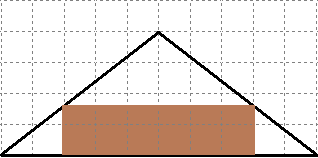 - Tenim una cartolina que fa 40 cm x 60 cm. Li tallem quatre quadrats, un per cada cantonada. Dobleguem per les línies de punts i obtindrem una capsa sense tapa. La pregunta que volem contestar és quina mida de costat del quadrat hem de tallar de manera que el volum de la capsa obtinguda sigui màxim. Busca (i explica) una estratègia per trobar-ho. 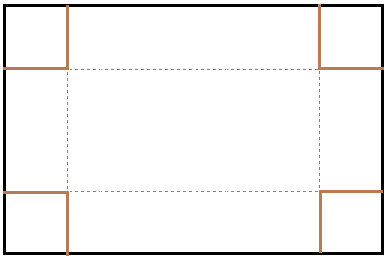 |