|
Conceptes i paraules, dues senzilles paraules Models, física, matemàtiques, intel·ligència, ciència, llenguatge, raonar, enraonar... són paraules que tot i no ser sinònimes estan molt relacionades i a vegades definim unes en funció de les altres. Parlaré del que vull parlar a partir d'un exemple, una pregunta, un problema que sortia a 2n de BUP a l'assignatura de Física i Química en el tema de cinèmàtica: Si disparem un canó que forma un angle amb l'horitzontal de 37º i la velocitat és de 350 m/s, quina és la distància que arribarà la bala suposant que el terra sigui horitzontal?  Segurament algú no li agrada l'exemple ja que fa referència a coses que ens poden semblar desagradables i que malauràdament d'alguna manera o altre, desgraciadament, hi hem de continuar convivim. Té una raó històrica el fet de fer aquest problema ja que se'l va plantejar i d'alguna manera, resoldre, Galileo, sentant les bases del que és la ciència tal com l'entenem avui dia. per fer el problema més soportabñe podem penar que hem de llençar un menjar a l'altre costat d'un riu i ens preguntem si arribarà. i) Anem per la solució del problema. Hi ha un model matemàtic que diu que el temps que estarà la bala volant és: On `v_i=350 m/s` és la velocitat inicial, `g=9'81 m/s^2`, l'acceleració de la gravetat i `\alpha=37º`, l'angle que forma el canó amb l'horitzontal. I la distància recorreguda és: Ajuntant les dues coses tenim una fórmula matemàtica, model, que conegudes unes dades `v_i, \alpha` i `g` ens permet predir la distància on arribarà la bala: Si hi posem números: Acabem de descobrir que un model matemàtic ens permet predir en el, què passarà si? ii) Però encara pot ser més potent en la seva predicció. Imaginen que volem fer arribar la bala a `8000` `metres`, el model ens pot dir com hem de posar el canó, o sigui, quin angle ha de formar el canó amb l'horitzontal perquè la bala arribi exactament a `8` `km`. Per fer-ho només cal aillar l'angle de l'anterior equació, salto els passos: Que en el nostre cas és: iii) Però la cosa pot anar molt més lluny. Ens podem preguntar, quin és l'angle que cal disparar el canó perquè las distància sigui la més gran possible i quina és aquesta distància? Per resoldre-ho farem servir un artilugi matemàtic que es diu, la derivada d'una funció, que quan val `0` ens dona el màxim (estrictament parlant un extrem). Fent servir unes transformacións de fórmules trigonomètriques la fórmula pot quedar més simplificada: La derivada de la qual és: Que igualada a `0` ens surt com a resultat, `cos(2\alpha)=0 => \alpha=45º` O sigui, si posem el canó amb un angle de `45º` respecte el terra, la bala arribarà més lluny. iv) I si fem servir un altre artil·lugi matemàtic que és la representació d'una funció podem veure una gràfica on veiem totes les distàncies que s'assoleixen en funció de l'angle. 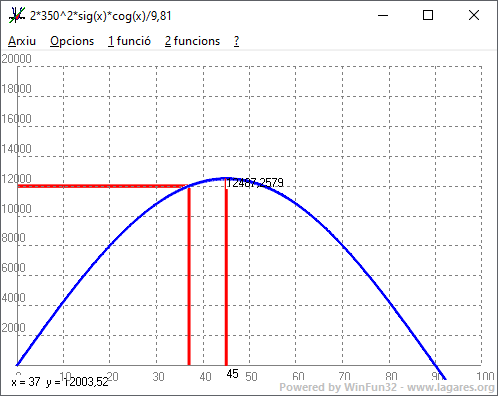 v) I finalment, com és que podem saber a quina velocitat surt la bala del canó. Doncs el problema va al revés, si disparem el canó amb un cert angle i sabem la distància assolida podem saber a quina velocitat a sortit la bala. Aixó doncs si disparem amb un angle de 37º i la bala arriba a 12053 metres aillant a l'equació la velocitat, podem saber a quina ha sortit del canó. Que en els nostre cas: En resum, el nostre model matemàtic, la fórmula que ens dona la distància en funció de l'angle i la velocitat inicial ens permet, calcular, predir, moltes coses. Cal dir que aquest model és una primera molt bona aproximació i s'ha de tenir en compte que hi ha altres factors que fan que els resultats no siguin del tot exactes i que s'haurien de tenir en compte per obtenir una molt millor aproximació als resultats reals. Esmentar-lo:
Com anècdota dir que vaig fer la mili a artilleria (Ramix32, Melilla) i que mai els meus coneixements balístics van ser fets servir. De fet mai no vaig disparar, ni vaig veure disparar, cap canó.  Com ho va fer Galileu per arribar a aquest model? Va fer experiments amb plans inclinats i deixant anar un objecte intentant que la superfície fos el més lliscant possible i se'n va adonar que si, en un interval de temps donat, el primer, recorria una certa distància, el segon mateix interval recorria `3` vegades la primera distància i el tercer mateix interval ecorria `5` vegades la primera distància. Si ho posem en una taula. $$ \begin{pmatrix} Interval & distància\\\ 1r & 1\\\ 2n & 3\\\ 3r & 5\\\ 4t & 7\\\ 5t & 9\\\ 6t & 11\\\ 7t & 13 \end{pmatrix} $$ Si ara el que fem és posar la distància total recorreguda fins: $$ \begin{pmatrix} temps & total\\\ 1 & 1\\\ 2 & 4\\\ 3 & 9\\\ 4 & 16\\\ 5 & 25\\\ 6 & 36\\\ 7 & 49 \end{pmatrix} $$ Observem que la distància en funció del temps segueix una fórmula proporcional al quadrat del temps. `d(t)=t^2` Si en lloc de fer servir un pla inclinat fem caiguda lliure (la llegenda diu que en Galileu va fer servir la torre inclinada de Pisa per fer les mesures de la caiguda d'un cos, tot i que en caiguda lliure de seguida els resultats no concorden degut a la forta força de frenada que fa l'aire), i fent servir les unitats actuals de mesura, segons i metres (recordeu que en època de Galileu encara, "1564-1642", no s'havia inventat el metre "circa 1800", la fórmula de la distància recorreguda en funció del temps, en el vuit, és: `d(t)=1/2g·t^2` Això es pot demostrar, per culpa de la dictadura de les matemàtiques, que correspont a un moviment amb acceleració constant. En el nostre cas l'acceleració val `g`. A partir d'això (i unes cuantes lleis tiraniques de les matemàtiques* ;-) pot deduir la fórmula que hem fet servir abans: `d(\alpha)=(v_i^2·sin(2\alpha))/g` *Recordem que les lleis dictades pel govern de les matemàtiques són d'obligat compliment. ;-) |