1. (OIF febrero 01) Dos cuerpos A y B se mueven un contra otro con velocidades de 80 cm/s y 20 cm/s respectivamente. La masa de A es 140 g y la de B es de 60 g. Después de una colisión frontal elástica la velocidad de B es:
a. 20 cm/s.
b. 92 cm/s.
c. 1,2 m/s.
d. 8 m/s.
Resultado: c.
2. (OIF febrero 01) Una partícula de masa m = 1,0 kg está sometida a una única fuerza, resultando una aceleración que se muestra en la figura. El impulso mecánico recibidoo por la partícula es:
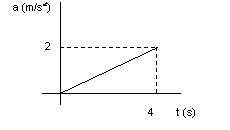
a. 0,5 N.s
b. 2 N.s
c. 4 N.s
d. 8 N.s
Resultado: c
3. (PAU junio 99) Es posible que en un cierto proceso se conserve la cantidad de movimiento de un sistema de partículas pero que no se conserve la energía cinética? Si la respuesta es negativa, razónalo. Si la respuesta es afirmativa, pon un ejemplo.
4. Un objeto de 20 g de masa que lleva una velocidad de 0,5 m/s choca con un segundo objeto de 50 g y que tiene una velocidad de 0,2 m/s en el mismo sentido que el primero. Calcula las velocidades de los dos cuerpos después del choque si éste es completamente elástico.
Resultado: 0,0714 y 0,3714 m/s
5. (PAU junio 99) Supon el caso ideal de un balón de tenis de 80 g de masa que choca contra una pared vertical y tanto antes como después de chocar va a 30 m/s y se mueve en la misma dirección horizontal. Se ha conservado la cantidad de movimiento del balón durante el choque? Cuanto vale el módulo del impulso realizado por la pared sobre el balón?
Resultado:
No
4,8 kg.m/s
6. Un cuerpo de 8 kg de masa tiene una velocidad de 10 m/s y choca frontalmente con un objeto de 12 kg que se encuentra parado. Si el choque es totalmente inelástico, calcula
a. La velocidad del sistema después del choque.
b. La pérdida de energía en el proceso.
Resultado:
4 m/s
240 J
7.
(PAU junio 03) Un proyectil
de 5 kg de masa se dispara con una velocidad inicial de 200 m/s y
con un ángulo de 45º con la horizontal. Suponiendo negligibles
los efectos del rozamiento, explica, razonándolo, si las magnitudes
siguientes se conservan a lo largo del movimiento:
a.
La cantidad de movimiento del proyectil.
b.
La energía mecánica del proyectil.
De las magnitudes que se conserven, calcula
su valor.
Resultado:
No se conserva
Sí se conserva, 105 J
8. Un muelle de constante elástica 2.000 N/m es comprimido 10 cm por dos bloques de masas 5 kg y 2 kg situados en sus extremos. El sistema se deja libre sobre una superficie plana sin rozamiento.
a. Cuál será la velocidad de salida de los dos bloques?
Resultado:
1,07 m/s
2,67 m/s
9. Un péndulo está formado por una masa de 3 kg situada en el extremo de un hilo de 1 metro de longitud. Inicialmente se sitúa el péndulo en posición horizontal y se deja caer. Cuando la masa pasa por el punto más bajo choca con otra masa de 200 g que va en sentido opuesto y con una velocidad de 10 m/s que se une a la primera.
a. Cuál será la altura máxima a qué llegará el conjunto de ambas masas?
b. Cuál es la tensión del hilo justo antes del choque?
c. Qué fuerza tiene que soportar el hilo justo después del impacto?
d. Qué energía se ha perdido en el choque?
Resultado:
0,63 m
138 N
71,64 N
19,61 J
10. Un camión (que viene del oeste) y un coche (que viene del sur) chocan inelásticamente en un cruce de calles perpendiculares. La masa del camión es de 8 toneladas y la del coche de 1,5 toneladas y sus velocidades son 36 km/h y 126 km/h respectivamente.
a. Cuál es la velocidad de la chatarra después del choque?
b. En qué dirección se mueve el conjunto?
Resultado:
10,06 m/s
33,24º
11. Un coche de 1.000 kg que va con una velocidad de 64,8 km/h en sentido norte choca con una moto de 120 kg que circula a 50,4 km/h y le sale de la derecha de una calle que hace 60º con la principal. El choque es totalmente inelástico.
a. Cuál será la velocidad del sistema coche-moto después del choque?
Resultado: 16,87 m/s
12. Una bala de 10 gramos penetra en un bloque de 5 kg y el conjunto comprime 3 cm un muelle de constante elástica 1.500 N/m. Si tenemos en cuenta que no hay rozamiento con el suelo,
a. Calcula la velocidad de la bala antes del impacto.
b. Cuál es la variación de energía mecánica de este choque?
Resultado:
260 m/s
337 J
13. Un cañón de 5 toneladas dispara un proyectil de 8 kg con un ángulo de tiro de 30 grados respecto la horizontal. El proyectil tarda ocho centésimas de segundo en recorrer el cañón y sale con una velocidad de 200 m/s.
a. Cuál será la velocidad de retroceso del cañón en dirección horizontal?
b. Cuál es la fuerza (normal) de reacción del suelo sobre el cañón?
Resultado:
0,28 m/s
60.000 N
14. (PAU junio 02) Dos patinadores, A y B, con la misma masa, m = 40 kg, se encuentran en reposo sobre una pista horizontal sin rozamiento apreciable. El patinador A lanza con una velocidad horizontal v = 2 m/s una bola de masa m = 6 kg que recoge el patinador B. Encuentra la velocidad final de cada patinador.
Resultado: -0,3 y 0,26 m/s
15. Dos partículas de 4 y 6 kg que van en sentidos contrarios chocan frontalmente con velocidades de 8 y 12 m/s y rebotan de modo perfectamente elástico.
a. Cuáles son las velocidades después del choque?
Resultado:
-15,25 m/s
3,5 m/s
16. (PAU junio 02) En un choque unidimensional, una bola de 5 kg se dirige hacia la derecha con una velocidad de 7 m/s y colisiona contra otra bola de 8 kg que inicialmente está en reposo. Después del choque, la bola de 5 kg va hacia la izquierda con una velocidad de 1 m/s y la bola de 8 kg va hacia la derecha con una velocidad de 5 m/s.
a. Investiga si el choque es elástico o inelástico.
b. Comprueba si se conserva la cantidad de movimiento.
Resultado:
Inelástico
se conserva
17. Un objeto de 3 kg se encuentra situado en el límite de un desnivel vertical de 3 m de altura cuando un bloque de un kilogramo que lleva una velocidad de 5 m/s choca elásticamente con él y le hace caer.
a. A qué distancia de la vertical caerá el bloque de 3 kg?
Resultado: 1,96 m
18. (PAU) Sean dos satèl.lits A y B de masas iguales m que se mueven en la misma órbita circular alrededor de la Tierra, que tiene masa M , pero en sentidos de rotación opuestos y, por tanto, en una trayectoria de choque. El periodo de rotación, T, de los satélites es de 24 h.
a. Demuestra que el radio de la trayectoria satisface la ecuación r 3 = G . M (T/2p)2 .
b. Cuáles son la velocidad y la energía mecánica de los satélites antes del choque?
c. Si, como consecuencia del choque, un satélite se incrusta en el otro, cuál será la velocidad del cuerpo de masa 2m después del choque?
d. Qué movimiento seguirá después del choque el cuerpo de masa 2m que resulta? Cuanto vale la pérdida de energía mecánica?
Datos: m = 100 kg; M = 5,98 . 10 24 kg; G = 6,673 . 10 –11 N.m 2/kg 2
Resultado:
3.073 m/s
- 4,72.108 J
0 m/s
- 9,44.108 J
19. (PAU junio 97) Una granada de 4 kg, inicialmente en reposo, explota en tres fragmentos. Dos de ellos tienen la misma masa y salen con velocidades que tienen el mismo módulo (v = 5 m/s) pero direcciones perpendiculares. El tercer trozo tiene masa triple que cada una de las otras dos.
a. Cuanto vale la cantidad de movimiento de la granada antes y después de la explosión?
b. Con qué velocidad sale el tercer trozo?
c. Calcula la energía mecánica de la granada generada como consecuencia de la explosión. Cuál es el origen de esta energía?
Resultado: 26,62 J
20. (PAU junio 98) Un cuerpo en reposo estalla y se divide en dos partes. Justifica que las velocidades de las dos partes tienen que tener la misma dirección. Las velocidades, tendrán el mismo sentido o sentido opuesto?
21. (PAU junio 98) Dos coches de masas M1 = 800 kg y M2 = 600 kg se mueven en direcciones perpendiculares. El primero, con velocidad horizontal v1 = 36 km/h y el segundo, con velocidad vertical v2 = 18 km/h. Los coches chocan de modo totalmente inelástico.
a. Cuáles son los componentes del vector cantidad de movimiento total antes y después del choque?
b. Cuál es la velocidad (en módulo y dirección) del conjunto de los dos coches después del choque?
c. Cuanta energía se ha perdido en el choque?
Resultado:
8.000 kg.m/s i + 3.000 kg.m/s j
6,10 m/s y 20,55º
- 21.453 J
22. (PAU junio 98) Dos cuerpos con la misma masa, que tienen velocidades de igual módulo (v= 10 m/s) e igual dirección pero sentido opuesto, chocan frontalmente. En el dibujo se representan dos posibles situaciones para las velocidades de los cuerpos después del choque. Razona por qué ninguna de ambas es posible. (Las masas de los cuerpos son las mismas antes y después del choque.)
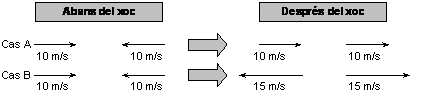
23. (PAU septiembre 97) Un patinador de 45 kg de masa que está parado enmedio de una pista de hielo lanza un disco de 500 g con una velocidad de 6 m/s. Qué velocidad tendrá el patinador inmediatamente después del lanzamiento?
Resultado: 0,066 m/s
24. (PAU septiembre 98) Un bloque de madera de 2 kg de masa está en reposo sobre una mesa. El coeficiente de rozamiento entre el bloque y la mesa es m = 0,8. El bloque está unido a un muelle que está fijado por el otro extremo. Un pequeño cuerpo metálico de 150 g de masa, con velocidad horizontal de 200 m/s, choca contra el bloque y queda incrustado en él. Suponiendo que el choque es instantáneo, calcula:
a. La velocidad del conjunto bloque-cuerpo inmediatamente después del choque.
b. La pérdida de energía mecánica en el choque.
c. Si la máxima compresión del muelle es de x= 90 cm, cuanto valdrá la constante elástica k del muelle?
Resultado:
13,95 m/s
- 2.790 J
516,5 N/m
25. (PAU septiembre 97) En una experiencia de laboratorio se deja caer verticalmente un balón de goma de 50 g sin velocidad inicial desde una cierta altura h y se mide la altura h' a la que sube después de rebotar en el suelo. La tabla de resultados es:
.h (cm) |
200,0 |
175,0 |
150,0 |
125,0 |
100,0 |
75,0 |
50,0 |
25,0 |
.h’ (cm) |
171,0 |
149,5 |
100,5 |
106,5 |
85,5 |
64,2 |
42,5 |
21,5 |
a. Rechazarias alguno de los datos? Por qué? Si se han medido con una regla milimétrica, cuál es el error relativo en la primera y la última de les medidas de h?
b. Es elástico el choque con el suelo? Como tendría que ser la tabla para poder afirmar que el choque es elástico?
c. Cuanta energía se ha perdido en la primera de les medidas de la tabla?
d. Si v es la velocidad justo antes de tocar al suelo y v' es la velocidad justo después, podríamos considerar que la relación v/v' es constante y darle un valor?
26. (PAU septiembre 99) Se lanza verticalmente desde tierra un cohete de 20 kg de masa. El cohete explota 10 segundos después, cuando su velocidad es de 102 m/s. Como consecuencia de la explosión se divide en dos fragmentos. El primero, que tiene un masa de 5 kg, sale con una velocidad de 50 m/s en la misma dirección y sentido con el que se movía el cohete en el momento de la explosión. Determina,
a. La velocidad con el que se arrojó el cohete y a qué distancia de tierra estaba en el momento de la explosión.
b. La velocidad del segundo fragmento inmediatamente después de la explosión (indica el módulo, la dirección y el sentido).
c. La energía cinética y la energía potencial gravitatoria del fragmento de 5 kg cuando hayan transcurrido 7 segundos desde la explosión.
Nota: supon constante la aceleración de la gravedad g = 9,8 m/s2.
Resultado:
200 m/s y 1.510 m
119,33 m/s vertical y hacia arriba
864,9 J y 1.619,9 J
27. (PAU junio 00) Un balón cae desde una altura H, choca elásticamente con el suelo y rebota de manera que sube hasta la misma altura H. Razona si como consecuencia del choque ha cambiado o no:
a. La cantidad de movimiento del balón.
b. La energía cinética del balón.
28. (PAU junio 00) Un cuerpo se mueve con una velocidad de 5 m/s. Si de golpe se rompe en dos partes iguales de manera que una de ellas se mueve con una velocidad de 2 m/s en la misma dirección y sentido que el cuerpo original, cuál será la velocidad (en módulo, dirección y sentido) de la otra parte?
Resultado: 8 m/s, misma dirección y sentido
29. (PAU junio 03) Un proyectil de 20 g va a una velocidad horizontal de 300 m/s y se empotra en un bloque de 1,5 kg que está inicialmente en reposo. Calcula la velocidad del conjunto inmediatamente después del impacto.
Resultado:
3,95 m/s
30. (PAU septiembre 00) Un jugador de fútbol, que está parado con el balón en los pies, pasa el balón a un compañero que se encuentra 15 m delante suyo y que se está alejando con velocidad constante en la dirección de la recta que une los dos jugadores. El balón tiene un masa de 400 g y sale de los pies del primer jugador con una velocidad de 20 m/s, formando un ángulo de 20º respeto el suelo. Calcula:
a. La máxima altura conseguida por el balón en su trayectoria.
b. La velocidad que tiene que llevar el segundo jugador para que el balón caiga a sus pies justo cuando éste llega al suelo.
c. Las componentes horizontal y vertical del impulso mecánico que el primer jugador ha comunicado al balón.
Resultado:
2,38 m
8,08 m/s
7,51 y 2,73 kg.m/s
31. (PAU septiembre 00) Se produce una explosión en un sistema aislado. Justifica cuál o cuáles de les siguientes afirmaciones son correctas:
a. No varía ni su cantidad de movimiento ni su energía cinética.
b. Varía su cantidad de movimiento pero no su energía cinética.
c. Varían su cantidad de movimiento y su energía cinética.
d. No varía su cantidad de movimiento pero sí su energía cinética.
Resultado:
F, F, F y V
32. (PAU septiembre 00) Se lanza una piedra de 20 kg de masa con una velocidad inicial de 200 m/s que forma un ángulo de 30º con la horizontal.
a. Cuanto valdrá su energía mecánica en el punto más alto de su trayectoria?
b. Cuál ha sido la variación de la cantidad de movimiento de la piedra al ir desde el punto de lanzamiento hasta el de máxima altura en su trayectoria parabólica?
Supon que cuando llega al punto de máxima altura la piedra se rompe en dos trozos de 5 kg y 15 kg, de manera que la masa de 15 kg queda parada inmediatamente después de la explosión.
c. Cuál sería la velocidad de la masa de 5 kg en este instante?
Resultado:
400.000 J
-2.000 kg.m/s
692 m/s
33. (PAU junio 01) Un atleta de 70 kg participa en una prueba de salto de longitud. Si en el salto el suelo le comunica un impulso de 680 N.s en una dirección que forma un ángulo de 20º con la horizontal, se pide:
a. Las componentes horizontal y vertical de la velocidad con la que el atleta salta del suelo.
b. La longitud del salto.
c. Si el atleta hubiese dado el mismo impulso en un lugar donde la gravedad fuese mayor, razona si la longitud del salto habría sido mayor, igual o menor.
Resultado:
9,13 y 3,32 m/s
6,06 m
Más pequeña

a. La velocidad del cañón inmediatamente después de salir el proyectil.
b. El espacio recorrido por el cañón sobre la plataforma como consecuencia del disparo.
c. La energía cinética con el que llega el proyectil al agua.
(Supone negligible la fricción con el aire.)
Resultado:
-2,4 m/s
1,47 m
1,82.106 J
35.
(PAU junio 03) Considera el sistema de la figura.
La masa m1 =
1,5 kg se encuentra inicialmente en reposo, en contacto con el extremo
de un muelle ideal de constante recuperadora k = 500 N/m, comprimida
30 cm. La masa m2 = 1,5 kg también se encuentra inicialmente en
reposo, a una distancia de 2 m de m1,
en la parte interior de una pista semicircular de radio R = 0,25
m. En el tramo horizontal que separa m1 de
m2, el coeficiente
de rozamiento es m = 0,2, mientras que en la pista semicircular el
rozamiento es negligible.
Cuando el muelle se deja ir, se descomprime e impulsa la masa m1, que se separa del muelle y choca elásticamente con m2. Calcula:

a.
La velocidad de m1 un instante antes de entrar en contacto
con m2.
b.
Las velocidades de ambas masas un instante después de entrar
en contacto.
c.
La aceleración centrípeta de m2 cuando llega
a la parte más alta del recorrido circular (punto B).
Resultado:
4,69 m/s
0 m/s y 4,69 m/s
48 m/s2