Una herramienta eficaz que tiene valor en sí misma.

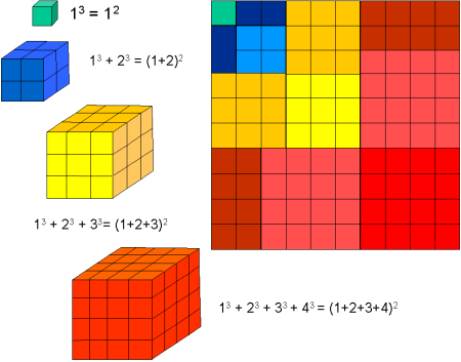
  En un curso de resolución de problemas para profesores se propuso primero inducir y después justificar qué valía la suma de los primeros n cubos

  En estos cursos coincidimos por una parte profesores de secundaria, con mucha “artillería pesada” para resolver, demostrar... y por otra un grupo de maestros que no tenemos los conceptos que ellos tienen y necesitamos crearlos cada vez, representando los números como cuadrados y cubos, acostumbrados a usar el “multilink   [3] ” y las “regletas numéricas de Maria Antonia Canals [4] ” ... Y a veces hay premio: la solución que resulta de la manipulación, de la imagen... tiene la ventaja de la claridad, de ser simple, elegante...

Primero abordamos el problema numéricamente. Y vimos que al sumar los cubos obteníamos el cuadrado de la suma.

1³+2³+3³ = (1+2+3)²

1³+2³+3³ .... + n³= (1+2+3.... + n)²

  Y luego se trataba de “convencer” y de convencernos de nuestra hipótesis.

La propuesta consistió en construir los cubos con multilink o regletas, y descomponerlos reconstruyendo el cuadrado.

   

 

Para acabar diría que usar la imagen y el material en clase de matemáticas tiene premio.

Como herramienta es potente. Y tiene valor por sí misma. Puede introducirse desde las primeras edades y dar fruto hasta niveles muy avanzados, incluso entre alumnos que no tienen conocimientos muy elevados. También es conveniente porque favorece la auto evaluación, la autocrítica, el análisis de los errores...

 No es por tener facilidad para visualizar, o para hacer equivalencias entre la numeración y la geometría... Es un aprendizaje. Y un aprendizaje útil. La mayoría de nuestros alumnos de primaria no siguen estudios superiores de matemáticas. No tendrán muchos conceptos previos adquiridos sólidamente, pero sí que pueden usar lo que tienen a mano si aprenden a usarlo. Y es lo que he aprendido en mi formación como docente. Volver a construir conceptos de primaria con otras herramientas cuando ya estamos preparados para entenderlos. Y además hacerlo con la “segunda intención” de enseñarlos a nuestros alumnos.