Mòdul 2
Aplicacions educatives de full de càlcul
Pràctica 12345678

 

Introducció

En aquesta pràctica us presentem:

  • La funció condicional SI.

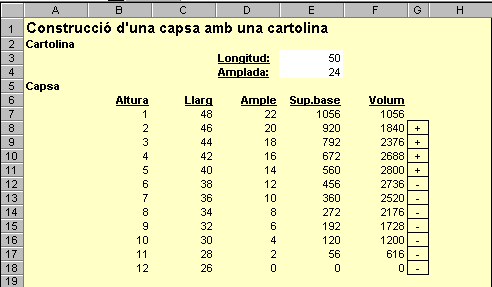
Es disposa d'una cartolina de 50 cm de llarg per 24 cm d'ample. Amb aquesta cartolina es vol construir una capsa sense tapa. Per fer-ho cal retallar petits quadrats iguals a les cantonades. Els costats d'aquests quadrats es transformaran en l'altura de la capsa. 

Construïu un full de càlcul que reflecteixi les dimensions de la capsa, la superfície de la base i el volum en funció del costat dels quadrats retallats. Això permetrà obtenir una primera informació de l'altura adequada per aconseguir un volum màxim. La figura adjunta és una possible solució:
 


Consideracions prèvies

Aquest és un problema que en matemàtiques s'anomena "de màxims i mínims". Per resoldre'l, en matemàtiques es farien servir eines de càlcul infinitesimal, com les derivades. En canvi, amb aquest full de càlcul en podem tenir una aproximació acceptable, pel mètode del tempteig. Cal remarcar que la solució que trobem és entera i la vertadera solució no té perquè ser-ho. A més, podem aconseguir simular diferents "capses", en variar les dades de les cel·les E3 i E4. 

Us trobareu per primer cop amb la funció SI( ; ; ). Vegem el seu significat. Si escrivim, SI (condició; expressió 1; expressió 2) en una cel·la, quan la condició s'acompleixi, es calcularà l'expressió 1; en cas contrari, l'expressió 2. Observant l'exemple de la pràctica, acabareu d'entendre el seu significat.
 
Desenvolupament de la pràctica
  • Seleccioneu un full del llibre MODUL2. Anomeneu-lo Capsa. 
  • Desactiveu la visió de la quadrícula. 
  • Introduïu les retolacions de les files 1, 2 i 5 amb els seus atributs. 
  • Introduïu a la cel·la D3, Longitud:. Introduïu a la cel·la D4, Amplada:. Doneu-li els atributs adequats. 
  • Introduïu a les cel·les E3 i E4 les dimensions de la cartolina (50 i 24 per exemple). 
  • Entreu-hi els rètols de la fila 6 i alineeu-les a la dreta per tal que quedin més centrades respecte als nombres que escriureu a sota. [1] 
  • Introduïu la successió d'altures 1..12 a les cel·les B7:B18. 
  • Introduïu a les cel·les C7, D7, E7 i F7 les fórmules per tal de calcular el llarg, l'ample, la superfície de la base i el volum de la capsa: 

    •  
    Cel·la
    C7 
    D7 
    E7 
    F7    		 Fórmula
    =E$3-2*B7 
    =E$4-2*B7 
    =C7*D7 
    =E7*B7
  • Copieu-les sobre el rang C8:F18. 
  • Introduïu a la cel·la G8 la fórmula =SI(F8>F7;"+";"-"). 

    •  
    Si el valor d'F8 és més gran que el d'F7, significa que el volum ha augmentat en passar el costat del quadrat d'1 a 2 cm. En aquest cas, hi escriurà un "+". En el cas contrari, escriurà un "-".
  • Copieu l'esmentada fórmula sobre el rang G9:G18.

    •  
    Analitzant la columna G pot observar-se amb rapidesa on hi ha un aparent canvi de comportament. Amb aquestes dades inicials (50 i 24), el volum màxim s'assoleix amb una altura igual a 5: és l'últim + de la columna G.
  • Doneu un fons groc clar al rang A1:H19. 
  • Dibuixeu un marc negre envoltant el full (rang A1:H19). 
  • Doneu un fons blanc a les cel·les E3 i E4 per tal de destacar que les seves dades poden ser modificades per tal de resoldre altres casos. [2] 
  • Seleccioneu el rang G8:G18 i emmarqueu els resultats de la comparació (+ o -). [3] 
  • Reduïu l'amplada de la columna G a 3 unitats i la columna H a 2 unitats. 
  • Centreu el contingut del rang G8:G18. 
  • Enregistreu el full. 
  • Modifiqueu l'amplada i la longitud de la cartolina (cel·les E3 i E4) i observeu el comportament del full. 
Com ja heu fet altres vegades, podeu anomenar algunes cel·les per tal que les fórmules siguin més entenedores ( veure pràctica 6 del mòdul 1):
  • Anomeneu les cel·les E3 com Longitud i E4 com Amplada.
  • Seleccioneu el rang B7:B18 i anomeneu-lo com Alt. En aquest cas totes les cel·les d'aquest rang tenen el mateix nom.
  • Feu el mateix amb les altres columnes i anomeneu-les Llarg, Ample, Base i Volum respectivament.
  • Accediu a Insertar | Nombre | Aplicar... i seleccioneu tots els noms que apareixen a la llista. Premeu Aceptar.
  • Observeu com han canviat les fórmules. Fixeu-vos que si en una fórmula es fa referència a un nom d'una de les columnes, les cel·les de les quals tenien el mateix nom, es considera el valor corresponent a la mateixa fila de la cel·la que conté la fórmula.
  • Enregistreu el full. 

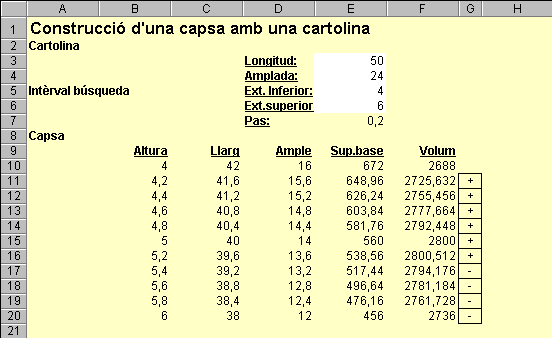
Suggeriment

Modifiqueu el full de càlcul anterior per tal que la gamma d'altures pugui ser variable permetent investigar amb major precisió el volum òptim. El valor del pas es dedueix dels extrems inferior i superior i del nombre de files del rang B10:F20 (11 a l'exemple). La figura següent descriu aquesta situació:

 


Aclariments
[1] Entreu-hi les retolacions de la fila 6 i alineeu-les a la dreta per tal que quedin més centrades respecte als nombres que escriureu a sota:
 
  • Seleccioneu-ne el rang B6:F6. 
  • Activeu els atributs negreta i subratllat. 
  • Seleccioneu l'opció Formato | Celdas | Alineación | Horizontal | Derecha. 

    •  
[2] Doneu un fons blanc a les cel·les E3 i E4 per tal de destacar que les seves dades poden ser modificades per tal de resoldre altres casos.
  • Seleccioneu el rang E3:E4. Activeu l'opció Formato | Celdas | Diseño. Trieu el color blanc del quadre de colors disponibles.

    •  
[3] Seleccioneu el rang G8:G18 i emmarqueu els resultats de la comparació (+ o -).
 
  • Per fer-ho activeu les opcions Contorno i Interior del menú Formato | Celdas | Bordes. Escolliu el color negre i l'estil de línia per defecte.

    •