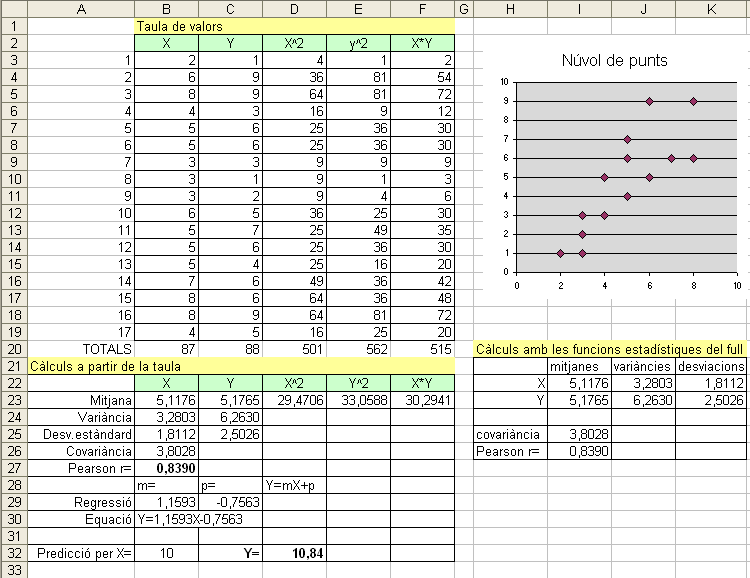
Indicacions per començar la feina:

Primer tindrem els valors de les dues variables entrats en dues columnes: columna X i columna Y.

A partir d'aquestes columnes farem la primera taula de valors afegint tres columnes més: una per x^2 (quadrat de X), una altra per Y^2 (quadrat de Y)i una tercera per X·Y.

Hem d'afegir una última fila per fer els totals de cada columna.

Recordeu que per entrar una fórmula en el full de càlcul heu de començar introduint el signe igual.

Càlculs a partir de la taula:

El primer que hem de calcular són les mitjanes de cada columna, dividint el total pel nombre de dades (en l'exemple són 17 dades N=17).

A continuació calcularem les variàncies de X i de Y restant la mitjana dels quadrats menys el quadrat de la mitjana. Recordeu que les desviacions estàndard (o típiques) són l'arrel quadrada de la variància. Podeu veure les fórmules matemàtiques en aquesta pàgina.

I ara vénen els paràmetres nous:

La covariància de X i Y es pot calcular fent la mitjana dels productes menys el producte de les mitjanes:

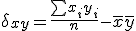El coeficient de correlació o de Perason és igual a la covariància dividida pel producte de les desviacions estàndard:

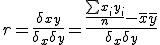La fórmula de la recta de regressió 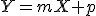s'obté calculant els coeficients m i p de la següent manera:

m=covariància dividida per la variància de x

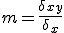p=mitjana de y menys m per mitjana de x

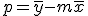Núvol de punts

Seleccioneu tots els valors de X i de Y i cliqueu l'assistent de gràfics. Cal seleccionar el tipus de gràfic "X Y (dispersió)".

Càlculs amb les funcions estadístiques

Tots aquests càlculs es poden fer més ràpid anant directament a aplicar les funcions estadístiques sobre les columnes de dades.

Les funcions, en la versió en español del programa, són les següents:

En cada cas B3:B19 s'ha de substituir per les referències a les cel·les que correspongui.

Mitjana arimètica:

=PROMEDIO(B3:B19),

Variància:

=VARP(B3:B19)

Desviació estàndard:

=DESVESTP(B3:B19)

Covariància:

=COVAR(B3:B19;C3:C19)

Coeficient de correlació, també anomenat de Perason:

=PEARSON(B3:B19;C3:C19)

Si voleu aprofundir més en les utilitats del full de càlcul podeu consultar aquest curs de Pep Bujoasa i Antoni Gomà "Introducció al full de càlcul".