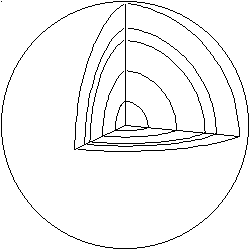
Fig.5.1. Aquesta seria l'evolució de la primera dimensió cap a la segona de la circumferència
Una de les grans dificultats amb la que ens hem enfrontat es troba en que en aquest cas no ens podíem basar ni en les arestes, ni els punts, ni les cares... per raons òbvies, de forma que vam buscar altres mètodes. Al final el que ens ha semblat més encertat és el referent al seus eixos.
Per començar tenim l'anomenat Gran Patriarca (un punt) a la dimensió inicial, la zero. El punt reuneix també la condició essencial de totes les figures que pertanyen a la família de l'esfera, o sigui, que tots els punts (en aquest cas només un) estan a la mateixa distància del centre de la figura.
A la primera dimensió, la lineal, perllonguem el punt central fins arribar a una recta, llavors trobem un segment, amb el punt central a la mateixa distància dels dos vèrtex, si treballem amb l'equivalent d'un cercle. Aquesta recta seria el primer eix, l'eix de la primera dimensió.

Un cop volem arribar a la tercera dimensió, fem girar els dos eixos de la segona en direccions diferents de l'espai, sortint del pla; entrant en la tercera dimensió. Després només ens cal unir tots els eus punts homòlegs. El resultat seria el mateix que fer girar una moneda, obtenint d'un pla un espai. Quan arribem a aquest punt tenim dues circumferències no superposades, que comparteixen una recta, en la que trobem el punt centre, llavors, si unim els punts homòlegs amb les corbes corresponents, on tots els seus punts han d'estar a la mateixa distància del centre, obtindrem l'esfera.

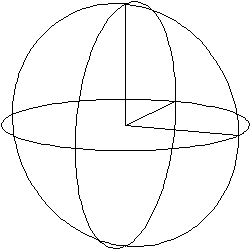
Ara només ens cal trobar un procediment per representar el THEMANSPHERAEKIE d'una forma diferent a l'esfera. El més senzill és dividir l'ésser tetradimensional en rodanxes. Per poder-ho fer amb precisió buscarem el mateix procès per a l'esfera i l'aplicarem a la quarta dimensió, deduint aquest sistema per analogies.
La pregunta és: Podem dividir d'alguna forma eficaç l'esfera? La resposta és senzilla: SÍ, igual que tallem a rodanxes el pa de pagès.
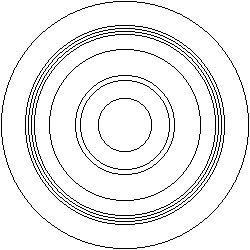
Per tant si el que volem és representar el THEMANSPHERAEKIE en tres dimensions el que haurem de fer és espaiar el seu volum, aixafar-la i ficar-la a les tres dimensions. Un cop fet aquest procés el que veiem són diferents esferes concèntriques de diferents radis, que van del de longitud igual a l'eix dimensional utilitzat inicialment a un radi de longitud zero. El resultat seria el següent: