1.3 Funcions polinòmiques
Una funció polinòmica és la relació entre dues variables x i y que té una fórmula del tipus y = anxn + an-1xn-1 + ... + a2x2 + a1x + a0
L'expressió anxn + an-1xn-1 + ... + a2x2 + a1x + a0 s'anomena polinomi. El nombre n és el grau del polinomi, i a0, a1, a2, ... an en són els coeficients. El coeficient a0 és el terme independent. El domini d’aquestes funcions és sempre tot el conjunt dels nombres reals.
Les gràfiques de les funcions polinòmiques
de primer grau y = ax+b, són rectes de pendent igual al paràmetre
a.
Quan a>0 són creixents i quan a<0
són decreixents.
Les gràfiques de les funcions y=ax, que expressen la proporcionalitat directa, són rectes que passen per l’origen de cooordenades.
Les gràfiques de les funcions polinòmiques de segon grau y = ax2+bx+c són paràboles. Quan a>0 són còncaves i quan a<0 són convexes.
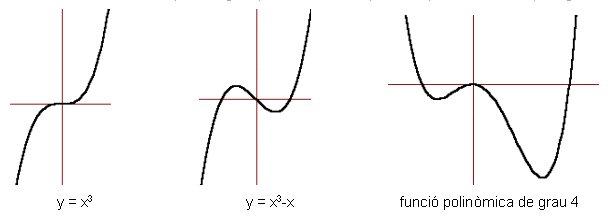
Aquí tens exemples de gràfiques de funcions polinòmiques de tercer i quart grau.
Els polinomis es poden sumar, restar i multiplicar
seguint les regles del càlcul algebraic. Dividir dos polinomis P(x)
i Q(x) és més complicat. Només es fa bé quan
Q(x) es de la forma x+a o x-a; llavors s'utilitza l'anomenat mètode
de Ruffini.
Per exemple, per dividir x3- 3x-2 entre
x-2 es fa: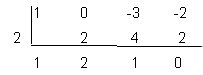 
i el quocient de la divisió és x2+2x+1.
Una igualtat de la forma P(x) = 0, o sigui anxn + an-1xn-1 + ... + a2x2 + a1x + a0 = 0, s'anomena equació polinòmica de grau n.
El càlcul exacte de les solucions d'una equació
polinòmica de grau més gran que 1 només pot fer-se
en alguns casos:
* Quan n=2 (equació de segon grau): si ax2+bx+c=0,
llavors 
* Quan n=4 i els coeficients de x i de x3
són 0 (equació biquadrada): si ax4+bx2+c=0,
llavors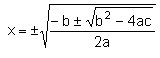 
Si l'equació és de grau 3 o més
gran cal fer:
1) obtenir els divisors del terme independent
2) comprovar si algun és una solució
3) si algun valor a
ho és, dividir P(x) entre x-a
emprant la regla de Ruffini
4) si Q(x) és el quocient, tornar al pas
(1) amb Q(x) i seguir així fins que el polinomi sigui de grau 2;
llavors es pot resoldre com una equació de segon grau.
Les equacions de grau parell poden no tenir cap solució, però els de grau senar sempre tenen alguna. El nombre total de solucions d'una equació és com a màxim igual al seu grau.
Quan una equació no té solucions enteres o no se sap com trobar-les es pot emprar un mètode aproximat anomenat mètode de Bolzano: si P(a)>0 i P(b)<0, llavors P(x) = 0 té una solució situada entre a i b
