1.4 Funcions racionals
Una funció racional és una
relació entre les variables x i y que té per
fórmula y = ![]() ,
on P(x) i Q(x) són polinomis, o que és una funció
polinòmica sumada o multiplicada amb una expressió d'aquest
tipus.
,
on P(x) i Q(x) són polinomis, o que és una funció
polinòmica sumada o multiplicada amb una expressió d'aquest
tipus.
Els valors d'una funció racional només poden calcular-se quan Q(x) és diferent de 0, és a dir quan x no és una solució de Q(x) = 0. Per tant el seu domini és R - {solucions de Q(x) = 0}
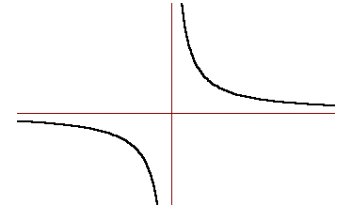
Les gràfiques de les funcions racionals són
molt variades. La més senzilla és de la funció ![]() , que s’anomena hipèrbola.
, que s’anomena hipèrbola.
Una equació racional és aquella
en què intervenen fraccions algebraiques. Per resoldre una equació
racional cal operar cada part (dreta i esquerra) de l'equació fins
reduir-la a la forma ![]() ; llavors es transforma en l'equació polinòmica A(x)D(x)
= B(x)C(x).
; llavors es transforma en l'equació polinòmica A(x)D(x)
= B(x)C(x).