1.5 Funcions irracionals
Una funció irracional és una
relació entre les variables x i y que té per
fórmula 
, on f(x) és una funció racional, o que és una funció
racional sumada o multiplicada amb una expressió d'aquest tipus.
El nombre n és l'índex de la funció irracional.
Les funcions irracionals més senzilles són 
.
Aquestes són les seves gràfiques.
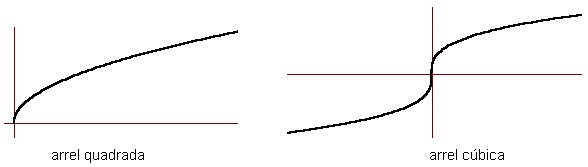
Els valors d'una funció irracional y =
quan l'index n és parell només poden calcular-se si f(x)>0
o si f(x)=0. Aquest és el seu domini. Per tal de saber quan
f(x) >0 cal seguir aquest procés:
1. Es troben els x tals que f(x) = 0.
2. Es troben els x en què f no es pot calcular.
3. Els valors de x així trobats són
els únics on f pot canviar de signe, i divideixen al domini de f
en zones de signe constant.
4. El signe de f a cada zona és el de qualsevol
dels seus valors en ella.
Per tal d'expressar aquestes zones s'utilitzen unes
notacions especials:
* Si a
i b són dos
nombres, es designa per [a,
b]
i s’anomena interval tancat d'extrems a
i b al conjunt de
nombres x tals que , i es designa per (a,
b)
i s’anomena interval obert d'extrems a
i b al conjunt de
nombres x tals que a
<x<b .
* Si a
és un nombre, es designa per (a,
+
) i s’anomena
semirecta
dreta d'origen a
al conjunt de nombres x tals que a<x,
i es designa per (- ,
a)
i s’anomena semirecta esquerra d'origen a,
al conjunt de nombres x tals que x<a.
El càlcul amb expressions irracionals (anomenades
radicals)
segueix les regles generals del càlcul algebraic i algunes d'especials:
a) multiplicació: 
Aquesta regla permet unir dues arrels multiplicades
del mateix índex, i també separar una arrel en dues; aquest
és el mètode de simplificar radicals.
b) divisió: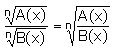 
c) potències: 
d) arrels: 
e) no hi ha regles per a la suma i la resta: 
no té cap relació amb 
El càlcul amb radicals té dos aspectes
principals:
a) La simplificació per extracció
de factors: 
b) El càlcul amb binomis radicals: 
Les equacions en què intervenen radicals són les equacions irracionals. Per resoldre-les cal separar un radical en una part (dreta o esquerra) de l'equació i elevar les dues al quadrat. Si encara queden radicals es repeteix el procediment. Quan ja han desaparegut, resta una equació polinòmica que s'ha de resoldre.
És molt important comprovar les solucions de les equacions irracionals.
