1.6 Funcions exponencials
S’anomena exponencial a una potència
ab,
on a i b són nombres reals i
a és positiu.
El nombre a rep el nom de base i
el nombre b el nom d’exponent.
Una exponencial pot interpretar-se de diferents
formes, segons quin sigui l'exponent.
* si b és natural, ab és
una multiplicació: ab = a·a·...·a
(b factors)
* si b és enter negatiu, ab és
una divisió: 
* si b és fraccionari, ab és
una arrel: 
El càlcul efectiu del valor aproximat d'una
exponencial es fa amb les tecles 
,
o anàlogues, de les calculadores.
La base més freqüent a les exponencials
que s'utilitzen a la ciència i a les matemàtiques és
la base e = 2,7182818286...
Les exponencials de base e poden calcular-se amb
una tecla especial de les calculadores, retolada amb ex.
Les regles de càlcul amb exponencials són les mateixes que amb potències:
La funció exponencial de base a és la relació entre dues variables x i y que té per fórmula y = ax
La gràfica de les funcions exponencials és d'un dels dos tipus següents:
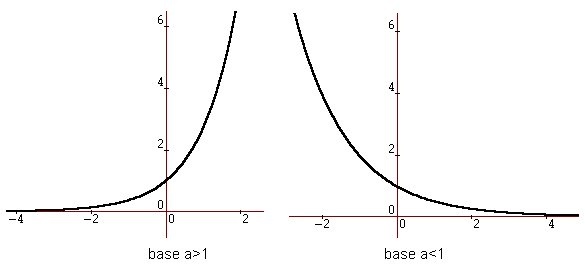
La importància de les funcions exponencials està en què descriuen tots els fenòmens en què una magnitud varia amb el temps amb un ritme de variació relativa constant. Això es veurà amb detall a la secció 1.10.
Les equacions en què intervenen exponencials
són les equacions exponencials. Els passos per resoldre-les
són:
* es transformen totes les exponencials que hi
figuren de forma que tinguin la mateixa base i el mateix exponent
* si l'exponencial única que queda és
ax, es pren com a nova incògnita t = ax
* es resol l'equació algebraica resultant
amb la incògnita t.
* per a cada solució t, el valor de x és
x = logat
