|
Probabilitats i nombres de Tartaglia
- Situem-nos en un cas senzill, en què juguen dues persones amb un dau. En Joan juga a l'1 i el 2, la Núria als altres números. Analitza les possibilitats que té cadascú de guanyar en la primera tirada. I després de dues tirades? Pots ajudar-te d'un còmput de possibilitats ...(J,N) (J,J)...
- Explica, amb l'ajut d'una situació o diagrama, si és certa la igualtat següent que correspon al joc de dues tirades. Utilitza la calculadora per veure que el resultat és cert i escriu una suma similar per a tres tirades de joc.
(J,J) (J,N) (N,J) (J,J)
(1/3)2 + (1/3)·(2/3) + (2/3)·(1/3) + (2/3)2 = 1
1·(1/3)2 + 2·(1/3)·(2/3) + 1·(2/3)2 = 1
- Observa com podrien haver sorgit els nombres que acompanyen les fraccions, i segueix la sèrie, anomenada de Tartaglia.
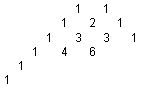
Recorda
Les probabilitats d'un mateix esdeveniment en dues tirades, s'obtenen per multiplicació de les probabilitats parcials de cada una. P(A,A) = P(A)·P(A).
Els nombres de Tartaglia corresponen al nombre de vegades que pot repetir-se un esdeveniment en un cert nombre de tirades. Cada nombre és un nombre combinatori. La suma de nombres combinatoris de la mateixa fila és 2n
|
Problemes
- Copia i completa el quadre següent:
Càlcul numèric
de probabilitat |
Fenomen corresponent explicat
amb jugades amb daus |
Nombre
Tartaglia |
| 2·(1/2)·(1/2) |
|
|
| 3·(1/4)·(3/4)2 |
Una vegada surt amb 1/4 de probabilitat......
i dues vagades....... |
|
| (1/2)2 |
|
|
| |
Surt parell tres vegades seguides |
1 |
Més coses
- Busca informació històrica sobre Tartaglia, Pascal i busca propietats en el triangle de nombre de l'activitat.
|