INTRODUCCIÓ I BIOGRAFIES DELS MATEMÀTICS RELACIONATS
Dintre d'un cicle de jornades
matemàtiques d'una Universitat catalana es donava una conferèn-cia
titulada "Les Matemàtiques durant el Renaixement", el ponent començà
la seva exposició dient:
- “U; u, u; u, ...
Sobtadament un dels assistents
exclamà en veu prou alta com per ser escoltat a la taula:
- ¡Vaya, nos ha tocado un “tartajas”!
Llavors el ponent, amb
molta calma, va reprendre la seva conferència:
- “Bé, com els anava dient, u; u u; u dos u; u tres tres u; ...
alguns de vostès ja s’hauran adonat que no es tracta d’un “tartajas”
sinó d’en Tartaglia, més concretament el conegudíssim
triangle de Tartaglia, atribuït també a Pascal o, en països
asiàtics, a Yang Hui. Sens dubte, es tracta d’una de les joies matemàtiques,
datat durant el Renaixement a Europa, amb el que volia començar
aquesta exposició ...”

· Blaise Pascal va néixer
a Clermont el dia 19 d'agost de 1623.
Era fill d’un insigne magistrat i estudiós
de problemes físics i matemàtics, va rebre la seva primera
formació del seu pare. El 1631 es traslladen a París i freqüentaren
el cercle d’intel·lectuals organitzat per Mersenne. Aviat es va
distingir per les seves investigacions en geometria i física. Als
15 anys publicà "Assaig sobre les còniques".
Sobre el 1646 es va adherir al jansenisme, fet
que marca per a ell, el començament de les seves preocupacions per
l’estudi del home, però sense abandonar el camp científic.
Va desenvolupar la teoria de les combinacions, creà les bases del
càlcul de probabilitats, i va estudiar la cicloide.
En física, va publicar l’obra “Nous experiments
en torn al buit” (1647) i va elˇlaborar el principi que porta el seu nom
i que diu: Tota pressió exercida sobre un líquid, es transmesa
per igual a tots els punts de la seva massa i actua perpendicularment sobre
las parets del recipient que el conté.
Va publicar un tractat sobre el tema que ens
ocupa "Triangle aritmètic" (1654)
L’any 1654 sent una profunda religiositat que
marcarà la resta de la seva existència i s’uneix al grup
de los solitaris de Port-Royal, un grup laic que vivia dedicat a la meditació.
El 1656 escriu, en contra de l’ortodòxia,
les seves cartes “Provinciales” que foren condemnades per l’Església.
El 1658 publica la seva obra pòstuma “Pensaments”.
Minvada la seva salut per una llarga malaltia
va morir el 19 d'agost de 1662 a París, just el dia del seu 39è
aniversari, reconciliat amb l’Església.
· Yang Hui
era un oficial menor xinès que va escriure dos llibres, datats al
1261 i 1275.
En ells, utilitza les fraccions
decimals (molt abans que a Occident), també apareix documentat el
triangle aritmètic.
La referència més
antiga al triangle aritmètic es atribuïda a Omar Khayyam, un
poeta, matemàtic i astrònom persa que, probablement, va precedir
Yang Hui, però no es té certesa de la data exacta de la seva
vida.
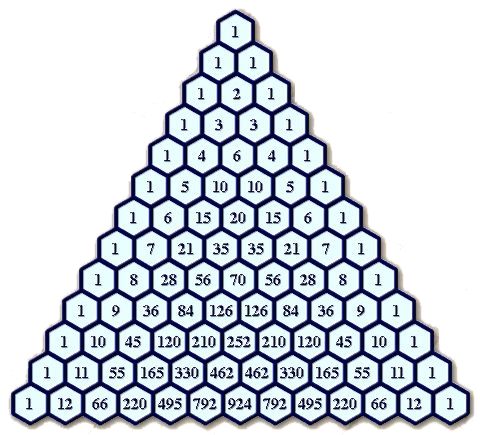
Com molt de vosaltres ja sabreu, aquest triangle
es genera a partir de situar el número 1 al seu extrem superior,
a partir d’aquí les successives files es construeixen col·locant
un 1 a cada cantonada i la resta de caselles és igual a la suma
dels dos nombres que té al damunt –observeu la figura- en una infinita
sèrie d’uns laterals i de sumatoris de caselles que produeixen un
incessant augment dels nombres que el composen.
Doncs bé, aquesta figura, que podria semblar
pels neòfits un simple entreteniment de càlcul, amaga una
diversitat de propietats i curiositats tan gran que el converteixen en
un petit univers matemàtic en sí mateix i una eina d’immensa
utilitat en el camp numèric, etc.
Els matemàtics de totes les èpoques,
des del seu descobriment, han posat els seus ulls en ell i han buscat tota
mena de sorprenents relacions, utilitats i recursos.
I a mi, que també m’ha encisat sempre
aquest triangle, m’ha portat a fer una petita investigació sobre
ell, fruit de la qual he trobat algunes cosetes interessants, apart de
les habitualment estudiades.
Començaré per parts, i aniré enumerant
i explicant les seves propietats més característiques:
- El número 1 de l’extrem superior del
triangle es considera com la fila zero.
- Cada número es genera a partir de la
suma dels dos nombres que té a sobre, com ja he dit.
Així, per exemple, els dos uns de la fila
1 sumats formen el 2 central de la segona fila.
La tercera fila es forma a partir del
1
+ 2 = 3 i 2
+ 1 = 3. La quarta és 1
+ 3 = 4, 3 + 3 = 6, etc.
- Totes les files mostren una estructura simètrica, les de ordre parell tenen un número central únic, les de ordre senar tenen dos nombres idèntics al centre. La suma de cada semifila imparell és, òbviament, igual.
- La suma dels nombres de cada fila és
igual a 2 elevat al número de la fila.
La quarta fila, per exemple:
1
+ 4 + 6 + 4 + 1 = 16 = 24. La sisena
1
+ 6 + 15 + 20 + 15 + 6 + 1 = 64 = 26
- Cada fila expressa les successives potències del número 11, les quatre primeres de forma clara, i a partir de la cinquena fila, si una casella està formada per més d'una xifra, hem de fer una senzilla suma portant-se alguna xifra. Exemples:
- Si ens situem a les files corresponents als
nombres primers observarem que es formen triangles invertits amb els seus
múltiples seguint un patró infinit i meravellós que
he intentat reflectir en aquesta il·lustració.
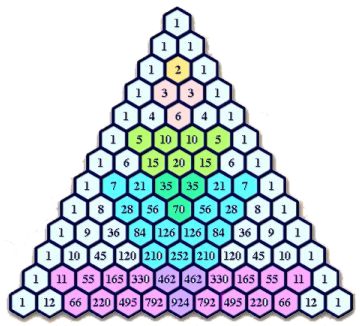
El nombre 11 per molt que no està complet
en el gràfic us garanteixo que també el forma i així
els successius nombres primers.
Es ben curiós que aquest patró
només es presenti en els nombres primers i no succeeixi amb la resta
de nombres, observeu com falla amb el nombres parells o amb el 9, el 15,
etc.
Podríeu donar una raó o demostració
per aquesta propietat. (Demostració)
- La suma dels nombres units per línies
roges, i situats a salt de cavall, formen la coneguda sèrie
de Fibonacci.
Vegem-ho: 1,
1, 1 + 1 = 2, 2 + 1 = 3, 1 + 3 + 1 = 5, 3 + 4 + 1 = 8, 1 + 6 + 5 + 1 =
13, 4 + 10 + 6 + 1 = 21, etc.
- Cada fila determina els coeficients que s’obtenen en desenvolupar les successives potències del binomi:
- Cada terme del triangle es pot expressar com el resultat del número combinatori:
Analitzaré ara les diagonals formades des de la part superior (amb colors a la il·lustració).
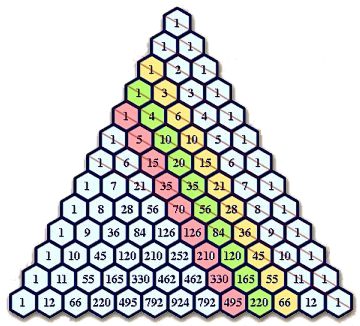
- La segona diagonal, situada al costat de la
diagonal formada pels uns exteriors, conté l'evident successió
de nombres naturals.
- La tercera diagonal, acolorida en groc, determina la sèrie de nombres triangulars:
De fet, demostra-ho és bastant senzill:
És a dir, també els nombres cúbics apareixen en el triangle aritmètic si sabem buscar-los.
Si prenem els nombres d'aquesta tercera diagonal de forma alterna, apareixen els nombres hexamòrfics:
- A la quarta diagonal, acolorida en verd i formada per la sèrie: 1, 4, 10, 20, 35, etc., si restem els nombres fent salts dobles (amb l'antepenúltim) apareix la sèrie de nombres quadrats, és a dir:
- A la cinquena diagonal, acolorida en vermell
i composta per la sèrie:
1, 5, 15, 35, 70, 126, etc., si restem els nombres fent salts
triples apareix la suma del quadrats màgics
d'ordre igual al lloc que ocupa el número a la sèrie, és
a dir:
15
- 0 = 15 (ordre
3, 3r núm. de la sèrie),
35 - 1 = 34(ordre
4, 4rt núm.), 70
- 5 = 65(ordre
5, 5è núm.)
- S’han estudiat a més altres de propietats numèriques del triangle, criteris de divisibilitat, algoritmes per a calcular els residus de les divisions, etc.
Analitzaré ara algunes relacions que existeixen
entre els nombres de les columnes centrals del triangle
aritmètic, el que jo denomino la columna vertebral de l’esmentat
triangle, i en la que he trobat dues propietats
molt importants:
- Si dividim la suma de cada fila pel valor central, en el cas de les files
d'ordre parell, o per un dels dos nombres centrals, en el cas de les files
d'ordre senar, obtenim valors que tendeixen a:

Els
nombres triangulars es generen geomètricament formant triangles
amb arestes que augmenten progressivament el seu nombre de punts, un exemple
fàcil d'imaginar és formar triangles amb monedes o amb boles
situades una sobre de l'altre.
Així necessitaríem 1 bola per formar un triangle d’una sola
fila, 3 per un de dues files, 6 per un de tres files, 10 per un de quatre,
etc.
L’algoritme que genera aquests nombres triangulars és: an
= n · (n + 1) / 2
Els Pitagòrics adoraven els nombres triangulars, fins i tot, antigament
tenien un cert valor místic.
Tenen moltes i molt curioses propietats, vegem-ne unes quantes abans de tornar
al tema:
· Cada número al quadrat és igual a vuit vegades un
número triangular més 1.
· Tot número triangular es pot expressar com la suma de tres
nombres triangulars. (Gauss)
· És possible trobar una infinitud de nombres triangulars
que multiplicats entre sí, el seu resultat
sigui un número al quadrat., etc.

Són els nombres
generats, geomètricament, al formar hexàgons continguts progressivament
uns a dintre dels altres. El nombre de punts necessaris per formar-los
són els nombres hexamòrfics.
L’algoritme que
permet calcular-los és: H(n)
= n · (2n - 1)
La sèrie
obtinguda és: 1, 6, 15, 28, 45, 66, 91, 120,
etc.
Imaginem un hexàgon
de 6 punts, un per aresta, a dins d’un més gran de 2 punts per aresta
(comparteixen alguns punts en comú) contingut a l’interior d’un
de 3 punts per aresta, etc.

Leonardo de Pisa, fill de Bonacci, i més conegut per Fibonacci, matemàtic del segle XIII va publicar la sèrie numèrica que porta el seu nom i que, començant per 1, 1, es genera sumant els dos nombres anteriors de la sèrie:
Aquests són
els primers vint-i-un termes de la sèrie de Fibonacci:
1, 1, 2, 3, 5,
8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4081, 6665,
10746

DEMOSTRACIÓ DELS TRIANGLES GENERATS PER NOMBRES PRIMERS
Si
utilitzem l'expressió general de les diverses xifres del triangle
aritmètic en funció dels nombres combinatoris veurem més
clara aquesta qüestió.
Cada terme del triangle
es pot expressar com el resultat del número combinatori:
DEMOSTRACIÓ DE LA SÈRIE DE NOMBRES AL QUADRAT DE LA QUARTA DIAGONAL
Per fer aquesta demostració expressaré
els valors de la diagonal en forma de nombres combinatoris (n sobre m),
la qual cosa em permetrà operar i simplificar ràpidament.
Observem que en aquesta diagonal per a cada valor
n,
tenim que m = n – 3, per exemple,
el 4 és n
= 4, m = 1, el 10 és n
= 5, m = 2, o el 20 és n
= 6, m = 3, etc.
Si restem dos termes d'aquesta diagonal separats
per dos salts i expressats en forma de nombres combinatoris, obtenim:
DEMOSTRACIÓ
DE L'APARICIÓ DE LA SUMA DELS QUADRATS MÀGICS
A LA CINQUENA DIAGONAL DEL TRIANGLE
ARITMÈTIC
Com hem vist en el capítol sobre els quadrats mŕgics, l’algoritme per obtenir la suma mŕgica S(x) de files, columnes i diagonals d’un quadrat mŕgic d’ordre n, compost per n2 nombres naturals, és:
Per fer aquesta demostració expressaré
els valors de la diagonal en forma de nombres combinatoris (n sobre m),
la qual cosa em permetrà operar i simplificar ràpidament.
Observem que en aquesta diagonal per cada valor
n,
tenim que m = n – 4, per exemple, el 5
és n = 5, m = 1, el 15 és n
= 6, m = 2, o el 35 és n
= 7, m = 3, etc.
Si restem dos termes d'aquesta diagonal separats
per tres llocs o salts obtindrem:
Els valors centrals d'un fila
n qualsevol
ocupen el lloc n / 2,
per a simplificar la demostració assignaré al número
de fila el valor 2n i,
per tant, al terme central la posició n.
La raó entre els dos nombres centrals
de dues files d’ordre parell consecutives, en forma de nombres combinatoris,
és:
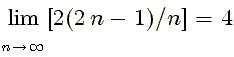

E-mail: mentaludix@hotmail.com