ACTIVIDAD 5.4
PROPIEDADES DEL PRODUCTO ESCALAR - 2

Menú inicial
Actividad anterior

Menú de la unidad 5
Actividad siguiente

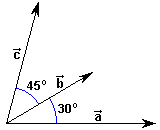
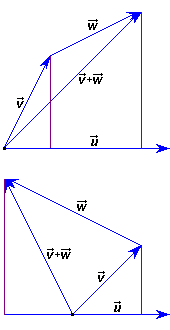
El producto escalar es distributivo respecto de la suma de vectores, es decir
                                       ·(+) = · + ·

Para demostrarlo tengamos en cuenta (ver la figura superior de la derecha):
1) En primer lugar, podemos calcular ·(+) haciendo el producto de || por la proyección de + sobre : ·(+) = ||(+)_|u
2) Ahora bien, como se puede ver en la figura, la proyección de una suma de vectores sobre otro vector es el mismo que la suma de las proyecciones:
                                      (+ )_|u = _|u + _|u
3) Enlazando las dos identidades anteriores, tenemos:
·(+)=||(+)_|u=||(_|u+_|u)=||_|u+||_|u=·+·

Se puede objetar que en la figura lo hemos preparado muy bien para poder hacer la afirmación 2). ¿Qué pasa si la proyección sobre de alguno de los vectores , o + tiene sentido contrario al de (tal como pasa, por ejemplo, en la figura inferior de la derecha)? Recordemos que estas proyecciones se hacen con signo y, por tanto, alguna proyección puede ser negativa. ¿Qué pasa entonces? Para responder a esta pregunta se ha preparado la siguiente actividad interactiva.

ACTIVIDAD INTERACTIVA

La figura de la derecha pone de manifiesto la distributividad
         ·(+) = · + ·

Comprueba que también se verifica esta distributividad cuando:

1) La proyección de sobretiene sentido contrario al sentido de .

2) La proyección de sobre tiene sentido contrario al sentido de .

3) Las dos proyecciones anteriores (de y de sobre ) tienen sentido contrario al sentido de .
                           SOLUCIÓN

FIN DE LA ACTIVIDAD 5.4
PROPIEDADES DEL PRODUCTO ESCALAR - 2

Menú inicial
Actividad anterior

Menú de la unidad 5
Actividad siguiente