Recordemos que los
dos vectores 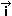 =(1,0)
y =(1,0)
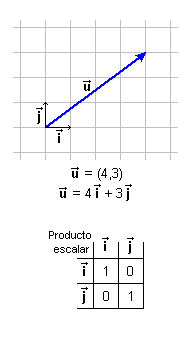
y 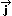 =(0,1) forman
una base de los vectores del plano y que cualquier vector =(0,1) forman
una base de los vectores del plano y que cualquier vector 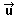 =(u1,u2)
se puede escribir =(u1,u2)
se puede escribir
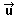 = (u1,u2)
= u1 = (u1,u2)
= u1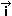 +
u 2 +
u 2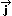
Tratemos ahora de calcular el producto
escalar de dos vectores  y
y  conocidas sus
componentes (en lugar de sus módulos y el ángulo
que forman): conocidas sus
componentes (en lugar de sus módulos y el ángulo
que forman):
 = (a1,a2)
= a1 = (a1,a2)
= a1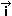 + a2 + a2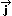
 =
(b1,b2) = b1 =
(b1,b2) = b1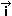 +
b2 +
b2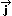
Utilizando las propiedades
vistas en las actividades anteriores, podemos escribir:
 · · =
(a1 =
(a1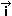 +
a2 +
a2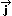 )·(b1 )·(b1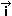 +
b2 +
b2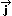 )
= a1b1 )
= a1b1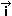 · ·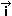 +
a1b2 +
a1b2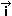 · ·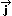 +
a2b1 +
a2b1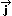 · ·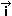 +
a2b2 +
a2b2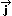 · ·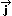
Ahora bien, cuando se multiplican escalarmente los vectores 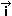 y
y 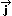 se verifica se verifica
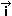 · ·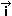 =
= 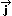 · ·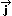 = 1
= 1
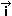 · ·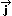 =
= 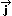 · ·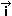 = 0
= 0
Substituyendo en la expresión
del producto escalar de  y
y  , obtenemos
un resultado muy importante que nos permite calcular directamente
un producto escalar de dos vectores conociendo sus componentes: , obtenemos
un resultado muy importante que nos permite calcular directamente
un producto escalar de dos vectores conociendo sus componentes:
 · · =
(a1,a2)·(b1,b2)
= a1b1+ a2b2 =
(a1,a2)·(b1,b2)
= a1b1+ a2b2
|
|
|
ACTIVIDAD INTERACTIVA
Tienes el producto escalar de dos vectores calculado aplicando
la fórmula
 · · =
(a1,a2)·(b1,b2)
= a1b1+ a2b2 =
(a1,a2)·(b1,b2)
= a1b1+ a2b2
Calcula los siguientes productos escalares y comprueba el resultado
utilizando este applet:
|
1) (4,1)·(2,3)
|
6) (3,0)·(0,3)
|
|
2) (3,-1)·(2,4)
|
7) (3,2)·(-3,-2)
|
|
3) (4,0)·(-2,3)
|
8) (3,2)·(-2,3)
|
|
4) (-2,3)·(1,-2)
|
9) (-3,-2)·(-2,3)
|
|
5) (2,1)·(4,2)
|
10) (3,2)·(2,-3)
|
SOLUCIÓN
|
|
Dados los vectores  =(3,4), =(3,4),
 =(1,-2), =(1,-2),  =(0,4)
y =(0,4)
y 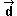 =(-3,1), calcula los siguientes
productos escalares: =(-3,1), calcula los siguientes
productos escalares:
a)  · · |
b)  · · |
c)  · ·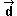 |
d)  · · |
e)  · ·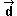 |
f )  · ·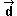 |
g)  2
= 2
= · · |
h)  2
= 2
= · · |
i ) 2 ·(3 ·(3 + + ) ) |
j ) ( + + )·( )·( + +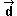 ) ) |
k) ( + + )2=( )2=( + + )·( )·( + + ) ) |
l ) ( + + )·( )·( - - ) ) |
Trata de calcular los productos escalares i), j),
k) y l) de dos formas diferentes.
|