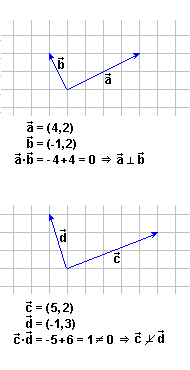
Según la definición que
hemos dado de producto escalar
 · =
||||cos(^)
tenemos que si dos vectores
y no nulos son
perpendiculares, su producto escalar es cero (ya que forman un
ángulo de 90º y cos90º = 0).
Recíprocamente, si el producto
escalar de vectores no nulos
i es cero, el
coseno del ángulo que forman ha de ser cero (pues no son
cero ni || ni
||), el ángulo
que forman es de 90º y los vectores son perpendiculares.
Este hecho nos permite dar la siguiente
definición:
dos vectores son perpendiculares (u ortogonales)
si
su producto escalar es cero
Simbólicamente, si indicamos la perpendicularidad con
^: ^ Û
·
= 0
Es interesante observar
dos cosas:
1) Recordando cómo se calcula el producto escalar a partir de
las componentes, la condición de perpendicularidad de dos vectores
dados por sus componentes es
=
(a1,a2) ^ =
(b1,b2) Û
·
= a1b1+ a2b2 = 0
2) Hemos extendido la definición de perpendicularidad a
vectores nulos, y según esta nueva definición, el
vector nulo es perpendicular a cualquier otro vector.
|
|
|
ACTIVIDAD INTERACTIVA
1) Utilitzando
·=
(a1,a2)·(b1,b2)
= a1b1+ a2b2
di cuales de los siguientes pares de vectores tienen producto
escalar cero y, por lo tanto, son perpendiculares. Compruébalo
en el applet de la derecha.
|
a) (4,1) y (1,4)
|
b) (4,1) y (-1,4)
|
|
c) (-1,2) y (4,2)
|
d) (3,2) y (1,-3)
|
|
e) (6,2) y (-1,3)
|
f) (5,2) y (0,0)
|
|
g) (3,2) y (-3,-2)
|
h) (6,-3) y (2,-1)
|
|
i) (2,1) y (4,5)
|
j) (3,0) y (0,-2)
|
2) Dibuja el vector =
(-2,3) y trata de dibujar dos vectores perpendiculares a .
¿Cuáles son sus componentes?
SOLUCIÓN
|
|
1) Obtén dos vectores
perpendiculares a cada uno de los vectores:
=
(5,6)
|
=
(-7,4)
|
 =
(-3,-1) |
 =
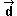(0,-3) |
2) Obtén dos vectores perpendiculares al
vector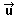 = (4,3) que tengan
módulo 10.
|
