Unit 5 - Activity 9

ACTIVITY 5.9
A THEOREM ATTRIBUTED TO THALES OF MILETUS FOUNDED AGAIN

One of the theorems more ancients known it is attributed to Thales (620-560 bC, aprox.). It isn't the classical theorem of Thales about the proportionality of the intercepted segments by a beam of straight parallel lines, but another that we are sure that you know:

An inscribed angle in a semi circumference is always right

We don't exactly know which type of proof made Thales of this theorem (not only if he demonstrated or he only announced it). We will make a proof using the scalar product.

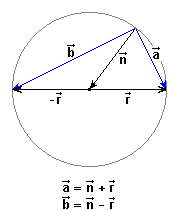Concretely, we will see that scalar product of two vectors and form this inscribed angle in the semi circumference is always zero; then we will be able to conclude that two vectors and are always perpendicular.

The proof is easy:
We will break down the vector in the sum =+, and vector in the remainder = -(see figure).
Then if we make the product ·, and we use the properties of the scalar product, we have

·= (+)·( -) =· - ·+ ·+·=² -² = ||² - ||² = 0

INTERACTIVE ACTIVITY

You have a PQR inscribed triangle in a semi circumference of radius 10. Two vectors and are perpendicular because its scalar product is zero. You can move R point on the circumference.

1) Locate R in points with whole coordinates, like R(8, 6), R(6, 8) and R(0, 10), and check that the scalar product of two vectorsand is always zero (therefore, they are perpendicular).

2) After locating R in point of not whole coordinates, check that this scalar product is zero or little value (should be zero, if not it is exactly the same, is because rounder that applet makes).

SOLUTION

HOMEWORK

(Do you want a Word document prepared for making this work ?)

Using scalar products, show you that two diagonals of a rhombus are always perpendicular.

Instruction: fix you in the figure, put the two diagonals ₁ and₂ like a linear combination of the vectorsand, calculate the scalar product ₁·₂ and check that it is zero.

Why this proof can't apply to a rhomboid?

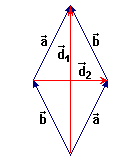END OF ACTIVITY 5.9
A THEOREM ATTRIBUTED TO THALES OF MILETUS FOUNDED AGAIN

Main menu
Previous activity

Menu of the unit 5
Next activity