Unit 5 - Activity 8

ACTIVITY 5.8
PROJECTION OF A VECTOR ONTO ANOTHER

Main menu
Previous activity

Menu of the unit 5
Next activity

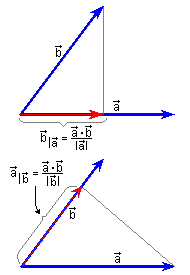
We remember that geometrically, the scalar product of two vectors is the product of the module of one of them by the projection of the other onto him (projection with sign , that is to say, negative if his directions is opposite to the first vector):

·

= |

|

_|a

In the other side, we can calculate the scalar product from the components:
·= (a₁,a₂)·(b₁,b₂) = a₁b₁+ a₂b₂

Making equal, we get ||_|a = a₁b₁+ a₂b₂

where we can isolate the projection of onto :
In a similar way we would get the projection of onto :

INTERACTIVE ACTIVITY

Calculate next projections (with sign and perpendicular) and check the result in the applet of the right side:

1) Of vector (1,5) onto vector (4,1)

2) Of vector (4,1) onto vector (1,5)

3) Of vector (-3,1) onto vector (2,2)

4) Of vector (2,2) onto vector (-3,1)

5) Of vector (1,2) on vector (4,-2)

6) Of vector (2,1) onto vector (4,2)

7) Of vector (-4,-2) onto vector (2,1)

HOMEWORK

(Do you want a Word document prepared for making this work ?)

We have seen that

gives the projection (with sign) of

onto

. If we want the projection vector of

ont

, we have to multiply the previous projection by a unit vector that it has the direction of the vector

. Like this vector is

, activity 3.7, vector projection of

onto

goes by :

Apply this procedure to calculate the vector projection of

onto

in the three next cases:

a)

= (1,5) and

= (4,1)

b)

= (-3,1) and

= (2,2)

c)

= (2,1) and

= (4,2)

END OF ACTIVITY 5.8
PROJECTION OF A VECTOR ONTO ANOTHER

Main menu
Previous activity

Menu of the unit 5
Next activity