|
- Saps què és això? (Pots clicar en la imatge) SOLUCIÓ: - Pots saber l'altura d'un triangle rectangle si sabem que la hipotenusa mesura 260 metres i la base en mesura 240?  SOLUCIÓ:
- Tenim un arbre que volem saber la seva altura. Per fer-ho ens allunyem del seu peu fins a que veiem el final de la copa amb un angle de 45°. Si la distància que ens trobem és de 14'23 metres. Pots dir quina és la seva altura, si l'alçada dels nostres ulls és de 1'68 metres? SOLUCIÓ: 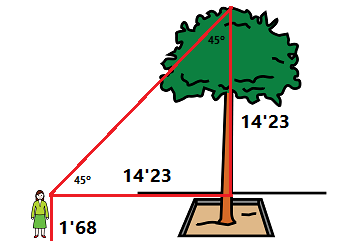
- Volem mesurar l'alçària d'un altre arbre, no podem fer el mateix ja que estem limitats per una paret i només podem allunyar-nos de l'arbre fins a veure'l amb un angle de 60°. Descobreix alguna manera de calcular la seva alçària sabem que la distància al seu peu és ara de 9 metres i l'alçada dels nostres ulls continua sent de 1'68 metres? SOLUCIÓ: 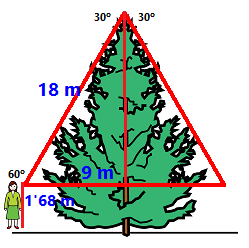
altura = `15'59+1'68=17'27` metres Amb els exercicis anteriors veiem que si es donen unes condicions determinades i fent unes fàcils mesures podem conèixer unes mides que per altra banda podien ser difícils de medir, com l'alçada d'un arbre. Però hi ha vegades que necessitem mesurar certes distàncies que és impossible fer-ho directament, com l'alçada d'una muntanya, ja que no podem fer un forat, ni tampoc un túnel.  Per la qual cosa, la matemàtica, ha inventat unes eines, les raons trigonomètriques, que ens peremetran realitzar aquestes mesures, inaccessibles, i d'altres encara més complicades com la distància d'aquí a la lluna, al sol, als planetes i a les estrelles. També per poder medir les distàncies que permeten construir carreteres, túnels, ponts, edificis, etc. Els propers exercicis serviran per aprendre què són i com fer-ho servir. Per aprendre què són el sinus, cosinus i la tangent d'un angle hagut pots fer servir els recursos externs que es mencionen en el índex d'aquest tema, o bé el teu professor. - Els radians és una altra forma de mesurar els angles (de la mateixa manera que per mesurar distàncies es pot fer amb km o milles,...). Ho sigui els angles es poden mesurar en ° i també en radians. L'únic que cal saber és que una volta sencera, 360° són 2Π radians. Fen servir regles de 3, pots contestar els següents preguntes?: a) Quants radians són 180°?`\pi` b) Quants radians són 90°?`\pi/2` c) Quants ° són 1 radià?`180/\pi=57'29577` d) Quants radians són 60°?`(\pi·60)/180=\pi/3` e) Quants radians són 30°?`(\pi·30)/180=\pi/6` f) Quants radians són 45°?`(\pi·45)/180=\pi/4` g) Quants radians són 150°?`(\pi·150)/180=(5\pi)/6` h) Quants radians són 270°?`(\pi·270)/180=(3\pi)/2` i) Sabries dibuixar més o menys un angle per cadascun dels valors anteriors? MOLT IMPORTANT: Les calculadores saben calcular les raons trigonomètriques de qualsevol angle expressat en ° (graus sexagessimals. Volta 360°). Graus centessimals (Volta 400°). No els fem servir). I radians (volta `2\pi`). És molt important que sàpigues configurar la calculadora en cadascuna de les tres maneres i sempre sàpigues en quin mode ho tens, ja que els resultats poden ser un disbarat si, per exemple, vols calcular un sinus(40°) i la calculadora està en mode radians. - Si tenim un triangle rectangle que la hipotenusa mesura 8 cm. la base 5 cm. Quant mesura l'altura (recorda un senyor grec molt famós anomenat Pitàgores)? Sabries calcular el sinus, el cosinus i la tangent de l'angle que formen la base i la hipotenusa? SOLUCIÓ: 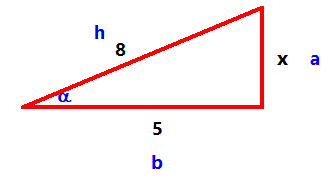
`5^2+x^2=8^2` `x = sqrt(8^2-5^2)= 6'25 ` cm`= a` `sin \alpha = a/h = (6'25)/8 = 0,78125` `cos \alpha = b/h = 5/8 = 0,625` `tan \alpha = a/b = (6'25)/5 = 1'25` - Amb l'ajuda de la calculadora pots dir quan mesura l'angle que forma la hipotenusa i la base del problema anterior? Quant mesuren els altres dos angles d'aquest triangle rectangle? SOLUCIÓ: 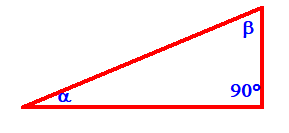
`\beta = 90-51'34=38'66` - Tenim una escala que mesura 4 metres recolzada a la paret formant un angle amb la horitzontal de 68°. Pots calcular a quina alçada està recolzada en la paret? SOLUCIÓ:
alçada = `a=4·sin 68=3'71` metres - Faig volar un estel amb una corda que mesura 45 metres i vola a una altura de 32 metres. Que pots dir quin angle forma la corda de l'estel amb la horitzontal? SOLUCIÓ:
`\alpha = sin^(-1)(32/45)=45'33°` - Si pugem a una muntanya amb un desnivell de 800 metres per una carretera de 10 kilòmetres. Quin és l'angle mig que té la carretera? 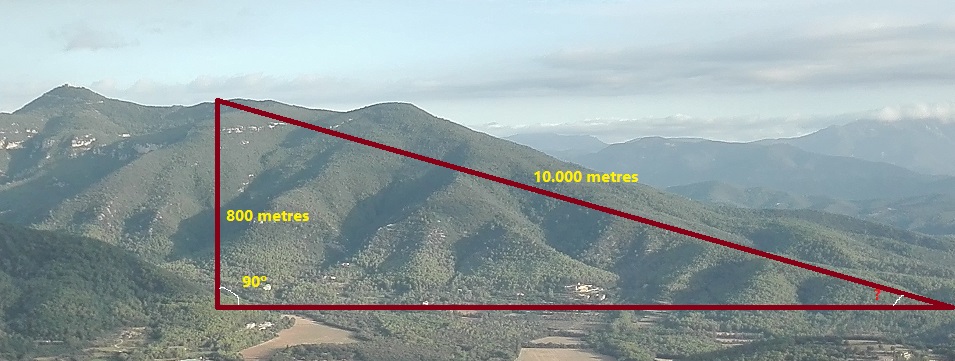 SOLUCIÓ:
`\alpha = sin^(-1)(800/10000)= 4'59°` - Si estic a una distància de 42 metres d'un edifici i des del terra veig la part més alta amb un angle de 38° respecte l'horitzontal. Saps calcular l'altura de l'edifici? SOLUCIÓ:
altura = `a=42·tan 38=32'81` metres - Al principi de la pujada a Rocacorba ens trobem amb aquest cartell: 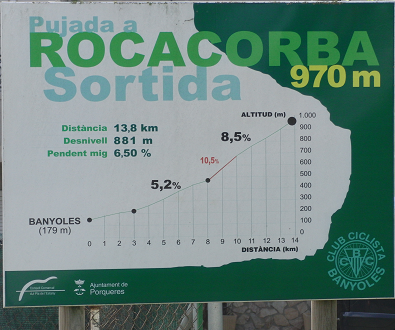 a) Saps explicar què significa el pendent mig? SOLUCIÓ:
b) Està ben calculat el pendent mig? SOLUCIÓ:
c) Quant val l'angle mig de la pujada respecte l'horitzontal? SOLUCIÓ:
`sin^(-1)(881/13800) = 3'66°` d) Hi veus algun error en el cartell? SOLUCIÓ:
- Un avió s'envola respecte l'horitzontal amb un angle de 28°. Si ho fa amb una velocitat de 60 metres per segon, a quina altura respecte a la pista es troba al cap de 12 segons? SOLUCIÓ:
`a/720 = sin 28` altura = `a = 720·sin 28 = 338` metres - A partir d'un triangle rectangle amb els catets iguals, amb l'ajuda del teorema de Pitàgores i una equació. Pots calcular el sinus, cosinus, i tangent de 45°? SOLUCIÓ: 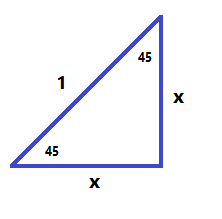
`2x^2=1` `x^2=1/2` `x=sqrt(1/2)=sqrt(2/4)=sqrt(2)/2`
`cos 45 = x/1 = x = sqrt(2)/2` `tan 45 = x/x = 1` - Dibuixa un triangle equilàter. Si el parteixes en dos triangles iguals, es pot calcular les raons trigonomètriques de 30° i de 60°. Ho saps fer? SOLUCIÓ: 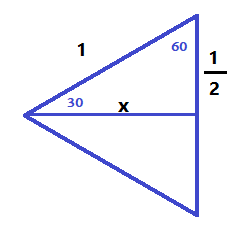
`x^2+1/4=1` `x^2=1-1/4=(4-1)/4=3/4` `x = sqrt(3/4)=sqrt(3)/2`
`cos 30 = x/1 = sqrt(3)/2:1 = sqrt(3)/2` `tan 30 = 1/2:x = 1/2:sqrt(3)/2=1/sqrt(3)=sqrt(3)/3` `sin 60 = x/1 = sqrt(3)/2:1 = sqrt(3)/2` `cos 60 = 1/2:1 = 1/2` `tan 60 = x:1/2 = sqrt(3)/2:1/2=sqrt(3)` - Sabries establir alguna relació entre les raons trigonomètriques d'un angle de manera que a partir del coneixement d'una es pogués conèixer les altres?. El teorema de Pitàgores et pot ajudar a fer-ho. SOLUCIÓ: 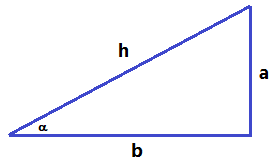
`a^2/h^2+b^2/h^2=h^2/h^2` `a^2/h^2+b^2/h^2=1` `sin \alpha = a/h` `cos \alpha = b/h`
`tan \alpha = a/b = (a/h)/(b/h) = sin \alpha/cos \alpha` - A partir del resultat anterior si tenim un angle que el seu sinus val 0'7, pots dir quant val el seu cosinus i la seva tangent?. SOLUCIÓ: `sin^2\alpha+cos^2\alpha=1` `tan \alpha = sin \alpha/cos \alpha`
`0'49+cos^2\alpha=1` `cos^2\alpha=1-0'49` `cos^2\alpha=0'51` `cos \alpha=sqrt(0'51)=0,71` `tan \alpha=sin \alpha/cos \alpha = (0'7)/(0'71)=0'99` - La resolució de l'equació del següent exercici és un xic més difícil, però no impossible. Si d'un angle sabem que la seva tangent val 2, pots dir quant val el seu cosinus i el seu sinus?. SOLUCIÓ: `sin^2\alpha+cos^2\alpha=1` `tan \alpha = sin \alpha/cos \alpha`
`2 = x/y` De la segona equació `2y=x` Substituim a la primera `(2y)^2+y^2=1` `4y^2+y^2=1` `5y^2=1` `y^2=1/5` `y=sqrt(1/5) = 0'45 = cos \alpha` `x=2·sqrt(1/5) =2·0'45=0'90 = sin \alpha` - Sabent que el cosinus d'un angle val 0'8, calcula les altres raons fent servir les relacions que hi ha entre les raons trigonomètriques. Pots dir de quin angle es tracta? SOLUCIÓ: `sin^2\alpha+cos^2\alpha=1` `tan \alpha = sin \alpha/cos \alpha`
`sin^2\alpha+0'64=1` `sin^2\alpha=1-0'64` `sin^2\alpha=0'36` `sin \alpha=sqrt(0'36)=0,6` `tan \alpha=sin \alpha/cos \alpha = (0'6)/(0'8)=0'75` `cos^(-1)(0'8) = 36'87°` - Sabent que la tangent d'un angle val 0'75, calcula les altres raons fent servir les relacions que hi ha entre les raons trigonomètriques. Pots dir de quin angle es tracta? SOLUCIÓ: `sin^2\alpha+cos^2\alpha=1` `tan \alpha = sin \alpha/cos \alpha`
`0'75 = x/y` De la segona equació `0'75y=x` Substituim a la primera `(0'75y)^2+y^2=1` `0'5625y^2+y^2=1` `1'5625y^2=1` `y^2=1/(1'5625)` `y=sqrt(1/(1'5625)) = 0'8 = cos \alpha` `x=0'75·0,8 =0'6 = sin \alpha` `sin^(-1)(0'6) = 36'87°` - Pots calcular les altres raons trigonomètriques d'un angle si ens diuen que el sinus de l'angle val 1'6. SOLUCIÓ: 
Per la mateixa raó, al cosinus li pasa el mateix. Relacions entre les raons trigonomètriques d'angles complementaris 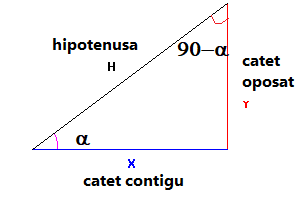 - Si et fixes que en un triangle rectangle els dos angles no rectes mesuren 90° (són complementaris). Sabries establir una relació entre les raons trigonomètriques de dos angles complementaris?. Pots ajudar-te amb un dibuix d'un triangle rectangle. SOLUCIÓ: 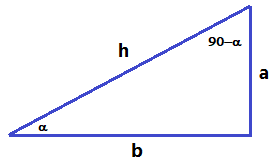
`cos(90-\alpha) = sin(\alpha)` `tan(90-\alpha) = 1/(tan(\alpha))`
`cos(19) = sin(71)` `tan(19) = 1/(tan(71))` Raons trigonomètriques d'un angle qualsevol - Mitjançant el programa Trigonometria (que pots descarregar en la plana anterior) es pot veure com es defineixen les raons trigonomètriques per qualsevol angle, o el teu professor que t'ho expliqui. O sinó aquí. Calcula, sin(32°); cos(58°), sin(90°), cos(105°), sin(173°), tan(123°), cos(180°), tan(180°), tan(90°), sin(195°), cos(195°), tan(195°), sin(270), cos(270), tan(270), sin(306°), cos(342°), tan(341°). - Fes una taula que la primera columna hi hagi sin, cos, tan i a la primera fila (a sobre) 0°, 90°, 180°, 270°, 360°. Escriu en cada casella el seu valor. SOLUCIÓ:
- Fes una taula que la primera columna hi hagi sin, cos, tan i a la primera fila (a sobre) 1r quadrant, 2n quadrant, 3r quadrant, 4t quadrant. Escriu en cada casella el signe de cada raó trigonomètrica. 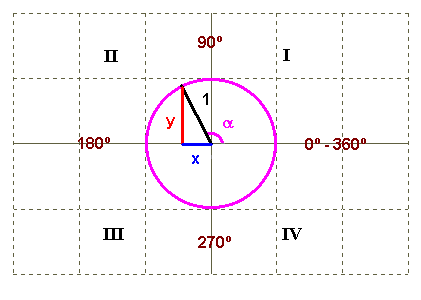 SOLUCIÓ:
- Fes una taula que la primera columna hi hagi sin, cos, tan i a la primera fila (a sobre) 30°, 150°, 210°, 330°. Escriu en cada casella la corresponent raó trigonomètrica. SOLUCIÓ:
- Mirant el que ha passat en el exercici anterior, si dic 40° (1r quadrant), podries dir quins angles dels altres quadrants passa el mateix? (o sigui que tenen les mateixes raons trigonomètriques en valor absolut). SOLUCIÓ:
- Mirant el que ha passat en els exercicis anteriors, si dic 160° (2n quadrant) podries dir quins angles dels altres quadrants passa el mateix? SOLUCIÓ:
- Indica les raons trigonomètriques de -40°, 385°, -185°, 835°, 934°, fent servir l'angle equivalent de la primera volta. SOLUCIÓ:
- Indica les raons trigonomètriques de -40°, 385°, -185°, 835°, 934°, fent servir l'angle equivalent del primer quadrant. Compte amb els signes. SOLUCIÓ:
`cos(-40) = cos 40` `tan(-40) = -tan 40` `sin 385 = sin (385-360) = sin 25` | 1r quadrant `cos 385 = cos 25` `tan 385 = tan 25` `sin (-185) = sin (-185+360) = sin 175 = sin(180-175) = sin 5` | 2n quadrant `cos (-185) = -cos 5` `tan (-185) = -tan 5` `sin 835 = sin (835-720) = sin 115 = sin(180-115) = sin 65` | 2n quadrant `cos 835 = -cos 65` `tan 835 = -tan 65` `sin 934 = sin (934-720) = sin 214 = -sin(214-180) = -sin 34` | 3r quadrant `cos 934 = -cos 34` `tan 934 = tan 34` - Saps dir les raons trigonomètriques dels angles següents fent servir raons trigonomètriques d'angles més petits que 45°. Angles: 63°, 168°, 250°, 835°. SOLUCIÓ:
`sin(63) = cos(27)` `cos(63) = sin(27)` `tan(63) = 1/(tan(27))` `168` (II "quadrant", sin + cos - tan -) `=> 180-168=12` que ja està al primer quadrant i més petit que 45 `sin(168) = sin(12)` `cos(168) = -cos(12)` `tan(168) = -tan(12)` `250` (III "quadrant", sin - cos - tan +) `=> 250-180=70 => 90-70=20` `sin(250) = -sin(70) = -cos(20)` `cos(250) = -cos(70) = -sin(20)` `tan(250) = tan(70) = tan(20)` `835 - 720 = 115` (II "quadrant", sin + cos - tan -) `=> 180-115=65 => 90-65=25` `sin(835) = sin(115) = sin(65) = cos(25)` `cos(835) = cos(115) = -cos(65) = -sin(25)` `tan(835) = tan(115) = -tan(65) = -tan(25)` - Amb el programa funcions dibuixa la funció sinus, f(x) = sig(x). Explica les seves característiques. (Origen eix X = -720; Unitat eix X = 90; Final eix X = 720) Nota: sig(x) és sin(x) en ° sexagessimals. SOLUCIÓ: 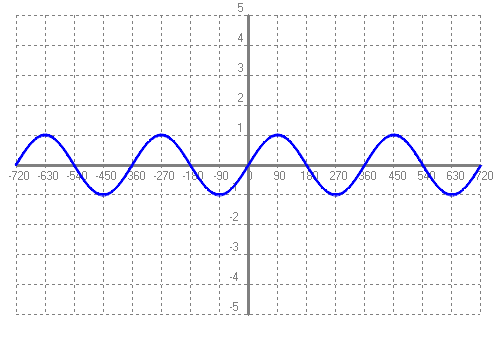
Els valors de les imatges (recorregut) va de `-1` a `1`, `[-1,1]` És una funció periòdica de periode `360º`. - Amb el programa funcions dibuixa la funció cosinus, f(x) = cog(x). Explica les seves característiques. (Origen eix X = -720; Unitat eix X = 90; Final eix X = 720). Compara-la amb la funció sinus del problema anterior, semblances i diferències? SOLUCIÓ: 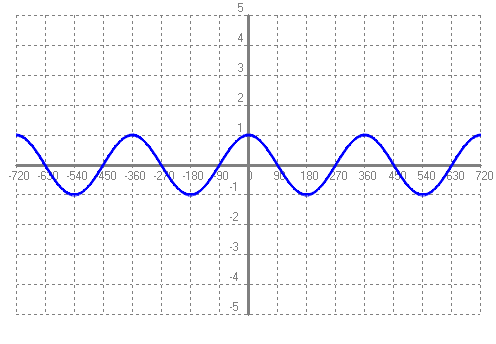
Els valors de les imatges (recorregut) va de `-1` a `1`, `[-1,1]` És una funció periòdica de periode `360º`. Te la mateixa forma que el sinus, però desplaçada `90º` a l'esquerra. Se'n diu desfase. - Amb el programa funcions dibuixa la funció tangent, f(x) = tag(x). Explica les seves característiques. (Origen eix X = -720; Unitat eix X = 90; Final eix X = 720) SOLUCIÓ: 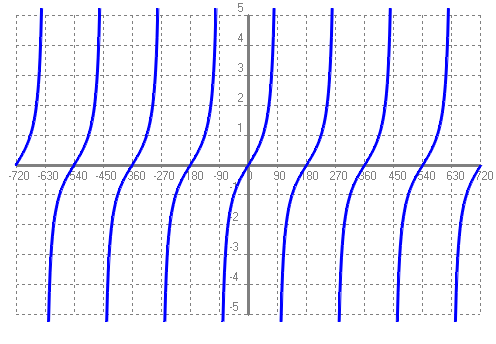
Els valors de les imatges (recorregut) va de `[-\infty,+\infty]` És una funció periòdica de periode `180º`. - Experimenta amb el programa funcions: Què passa si dibuixes la funció sig(2x) i sig(3x) i sig(4x). SOLUCIÓ: 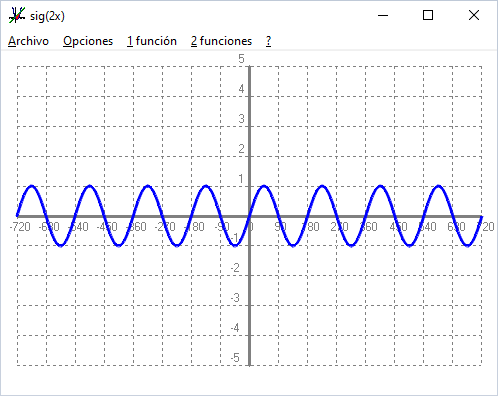 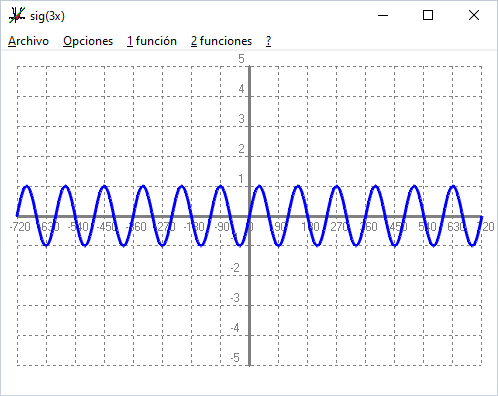 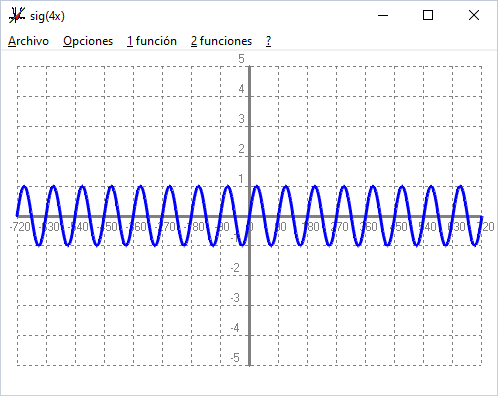
Però el periode en el primer cas és `1/2`, `180º`, en el segon, `1/3`, `120º`, i en el tercer, `1/4`, `90º`. Si ho mirem des d'un altre punt de vista veiem com més ones, la freqüència en el primer cas és el doble, en el segon, el triple, i en el tercer, `4` vegades més gran. - Experimenta amb el programa funcions: Què passa si dibuixes la funció 2sig(x) i 3sig(x) i 4sig(x). SOLUCIÓ: 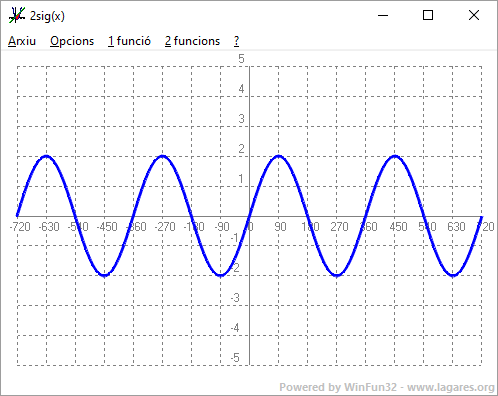 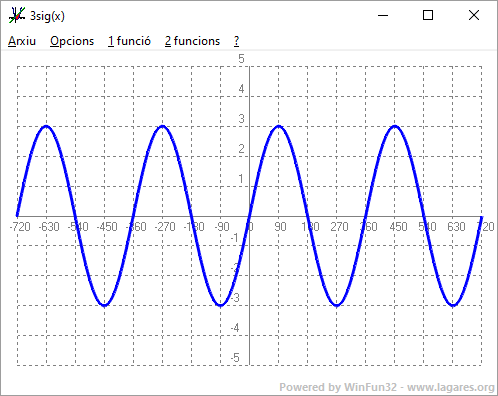 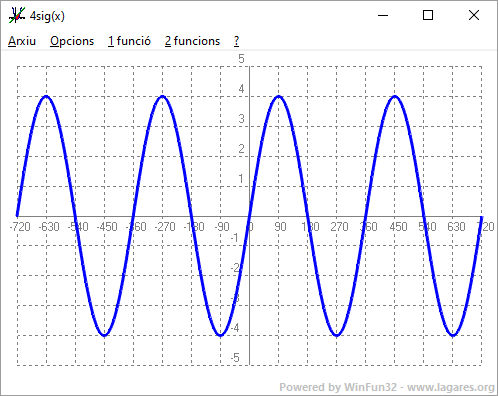
- Experimenta amb el programa funcions: Què passa si dibuixes la funció 2sig(3x) i 3sig(0,5x). SOLUCIÓ: 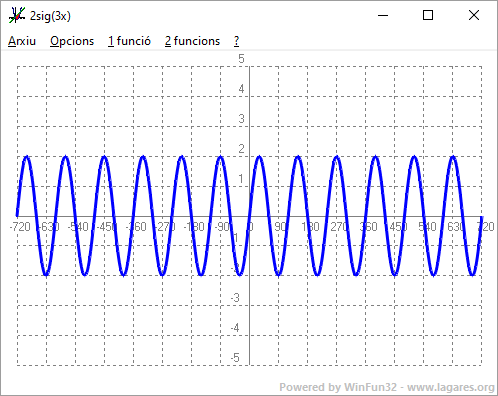 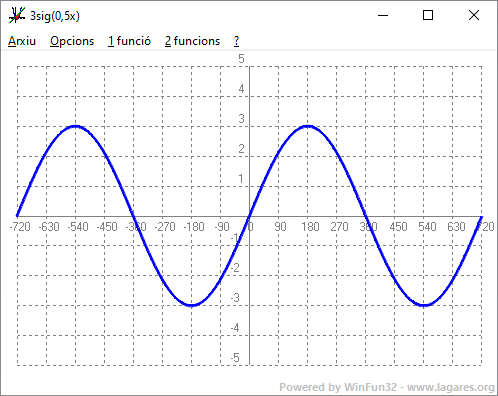
- Experimenta amb el programa funcions: Què passa si dibuixes la funció 2sig(x) + sig(2x) + 0,5sig(3x). SOLUCIÓ: 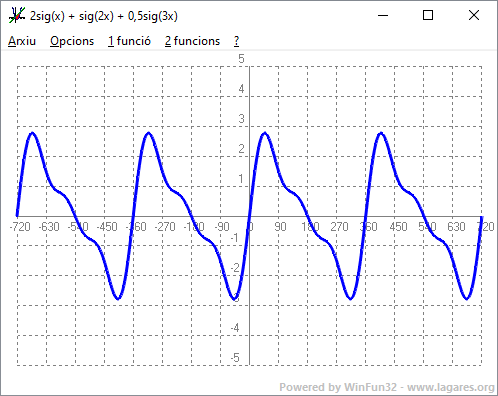
- Observa la següent funció:  Escolta-la: Amb el programa funcions dibuixa: (per veure-ho millor posa eix X Origen = -15 i Final = 15; eix Y Origen -10 i Final = 10. Pots activar la opció Treure eixos i disminuir la gruixudària de les línies). 0,17sin(x)+0,21sin(2x)+0,28sin(3x)+0,73sin(4x)+1,16sin(5x)+0,46sin(6x)+0,31sin(7x)+0,09sin(8x)+0,03sin(9x) SOLUCIÓ: 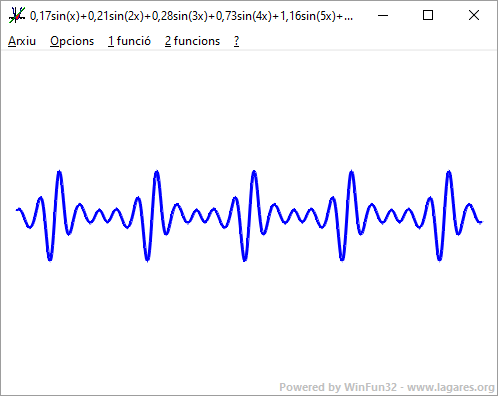
+ Exercicis d'aplicació a la geometria - Calcula el perímetre i l'àrea d'un quadrat inscrit en una circunferència de diàmetre 2 dm. SOLUCIÓ: 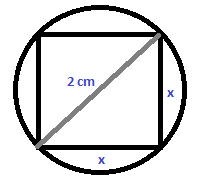
`x^2+x^2=2^2` `2x^2=4 => x^2=2 => x=sqrt(2)` Àrea `= sqrt(2)^2=2` `dm^2` - Calcula l'àrea d'un hexàgon inscrit en una circunferència de diàmetre 6 dm. SOLUCIÓ: 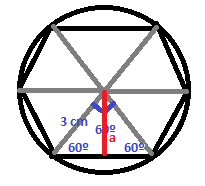 Per trobar el perímetre només ens hem de donar compte que un exàgon està composat per `6` triangles equilàters, ja que els tres angles són de 60º. La qual cosa implica que la base del triangle mesuri igual que el radi, `3` cm. Per calcular l'àrea necessitem l'altura del triangle i sabem que, `a/3=sin 60 => a=3·sin60 =2'6` cm - Resoldre un triangle vol dir conegudes algunes coses, per exemple dos costats i un angle, trobar lo altre, l'altre costat i els altres dos angles. Resol els triangles rectangles següents: 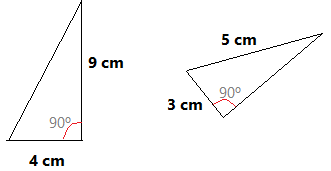 SOLUCIÓ: 1r triangle.
h `=sqrt(4^2+9^2)=sqrt(97) = 9'85` cm. Per trobar l'angle podem fer servir l'invers de la tangent. `alpha = arctan(9/4) = 66`º. Per trobar l'altre angle recordem que és el complementari de l'angle acabat de trobar. `beta = 90-66 = 24`º
`c=sqrt(5^2-3^2)=sqrt(16)=4` cm. Per trobar l'angle podem fer servir l'invers del sinus. `alpha = arcsin(3/5) = 36'87`º Per trobar l'altre angle recordem que és el complementari de l'angle acabat de trobar. `beta = 90-36'87 = 53'13`º - Calcula l'àrea d'aquest triangle. 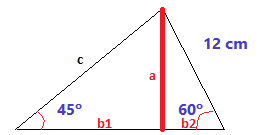 SOLUCIÓ:
`a/12=sin(60) => a=12·sin(60) = 10'39` cm Ara cal trobar la base, per fer-ho la dividim en dos trossos, `b_1` i `b_2`. Per trobar `b_2` podem fer servir el `cos(60)` `b_2/12=cos(60) => b_2=12·cos(60)=6` cm. Per trobar `b_1` podem fer servir la `tan(45)`.
Per la qual cosa la base del triangle val `b=b_1+b_2=10'39+6=16'39` cm. Per trobar el perímetre encara ens falta el costat `c`. Podem fer servir el `sin(45)`. tambého podriem fer amb Pitàgores.
El perímetre és la suma dels tres costats: I l'àrea: - Calcula l'àrea i el perímetre d'un triangle isòsceles que el seu costat desigual mesura 5 cm i l'angle repetit val 24º. SOLUCIÓ: 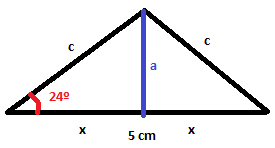 Si dividim la base en dos trossos iguals, `x = 2'5` cm. Per trobar l'altura podem fer servir la `tan(24)`.
Per trobar l'altre costat,`c`, podem fer servir el cosinus. també podríem fer servir Pitàgores.
El perímetre és la suma dels tres costats: I l'àrea: + Exercicis d'aplicació (mètode de la doble tangent) - Tornem a l'aplicació de les raons trigonomètriques per mesurar distàncies inaccessibles, per exemple, mesurar l'alçada de la mare de Déu del Mont. El que es fa és mesurar una distància d en un lloc que es pugui mesurar, i dos angles a i b. Es planteja un sistema de dos equacions amb dos incògnites i la seva solució serà l'altura de la muntanya i altres mesures que ens puguin interessar. 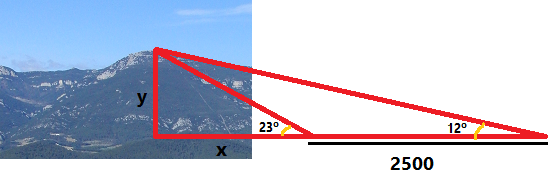 Si la distància = 2500 metres, l'angle a = 12° i l'angle b = 23°. Quant mesura l'altura de la muntanya? SOLUCIÓ:
`y/(x+2500)=tan(12)` `y=tan(23)·x` `y=tan(12)·(x+2500)` `tan(23)·x=tan(12)·(x+2500)` `tan(23)·x=tan(12)·x+tan(25)·2500` `tan(23)·x-tan(12)·x=tan(12)·2500` `(tan(23)-tan(12))·x=tan(12)·2500` `x=(tan(12)·2500)/(tan(23)-tan(12))` - Volem saber l'altura a que es troba la part de dalt de la creu que hi ha en una església. Per fer-ho agafem dos punts a cada banda de l'església separats 80 metres, si l'angle a mesura 56° i l'angle b mesura 38°. Quina és aquesta altura? 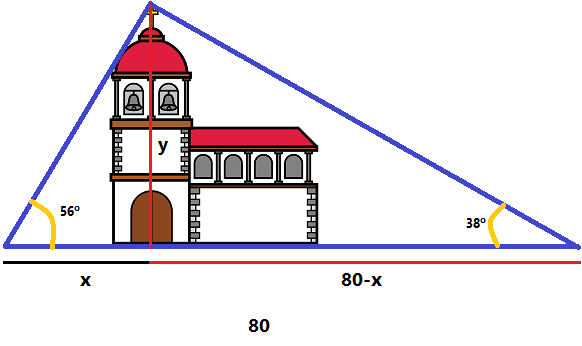 SOLUCIÓ:
`y/(80-x)=tan(38)` `y=tan(56)·x` `y=tan(38)·(80-x)` `tan(56)·x=tan(38)·(80-x)` `tan(56)·x=tan(38)·80-tan(38)·x` `tan(56)·x+tan(38)·x=tan(38)·80` `(tan(56)+tan(38))·x=tan(38)·80` `x=(tan(38)·80)/(tan(56)+tan(38))` - Si un avió entrant a pista per aterrar veu la capçalera de la pista amb un ngle (respecte a l'horitzontal) de 34°, el final de pista amb un angle de 25° i sabent que la longitud de la pista és de 2.500 metres, Es demana l'altura a que es troba l'avió en aquest moment i la distància a la capçalera de la pista. 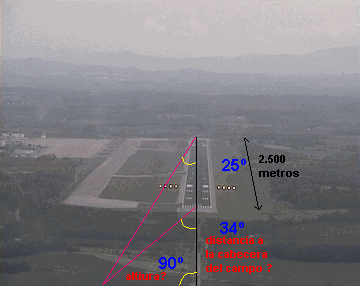 SOLUCIÓ: 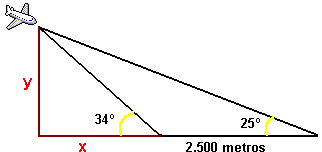
`y/(x+2500)=tan(25)` `y=tan(34)·x` `y=tan(25)·(x+2500)` `tan(34)·x=tan(25)·(x+2500)` `tan(34)·x=tan(25)·x+tan(25)·2500` `tan(34)·x-tan(25)·x=tan(25)·2500` `(tan(34)-tan(25))·x=tan(25)·2500` `x=(tan(25)·2500)/(tan(34)-tan(25))` - Tenim un riu que és difícil atravesar-lo i complicat mesurar la seva amplada en un punt on es vol construir un pont. Escriu l'enunciat d'un problema que ens permeti descriure lo anterior i ens permeti trobar la solució. Un cop hagis escrit l'enunciat, fes un esquema del que diu i resol el problema.  - Tenim un triangle isòsceles que un dels costats iguals, mesura 14 cm i l'angle diferent 25°. Calcula: els angles i el costat que no sabem, el perímetre i l'àrea. 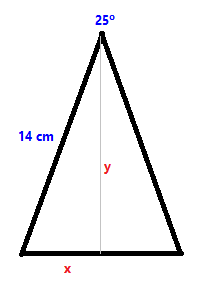
altura `= y/14=sin(77'5) => y=14·sin(77'5) = 13'67` cm mitja base `= x/14=cos(77'5) => x=14·cos(77'5) = 3'03` cm Base `=3'03·2 = 6,06` cm Perímetre `= 14·2+6'06 = 34,06` cm Àrea `= (13'67·6'06)/2 = 41'42` cm2 - Un canó dispara una bala a `750` `m/s`. Si l'angle que forma el tub del canó amb l'horitzontal és de 23º, calcula les velocitats horitzontal i vertical de la bala. Quan estudiïs cinemàtica podràs calcular coses com l'altura on arriba la bala i la distància on tocarà a terra.  SOLUCIÓ: 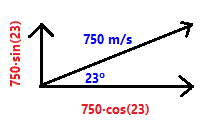
Velocitat vertical `= 750·sin(23)= 293 m/s` - Mira el dibuix. Sabries dir quan val l'angle `a`? I quant mesuren els costats del rectangle `x` i `y`? 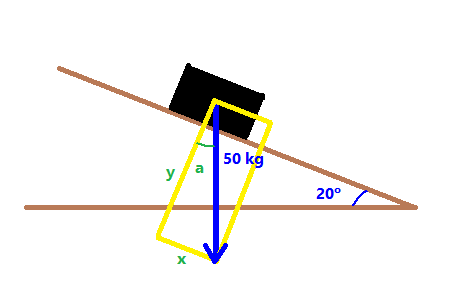 SOLUCIÓ: 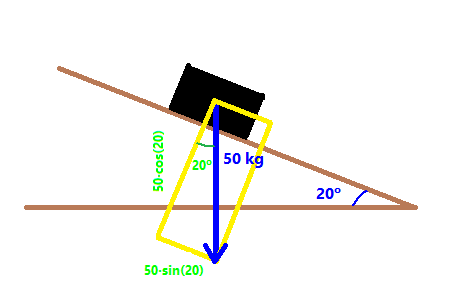 Component paral·lela al pla inclinat `= 50·sin(20)= 17'10` kg Component perpendicular al pla inclinat `= 50·cos(20)= 46'98` kg - Mira el dibuix. Suposem que l'objecte gris baixa pel pla inclinat, sense rozament, calcula l'acceleració en la que està baixant pel pla inclinat, suposant que l'acceleració de la gravetat és `9'8 m/s^2`. 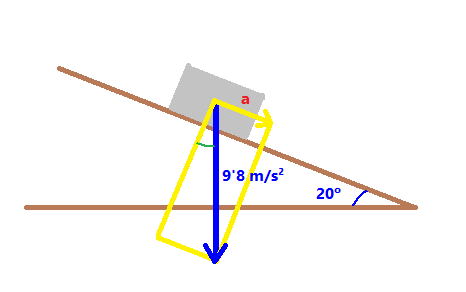 SOLUCIÓ: 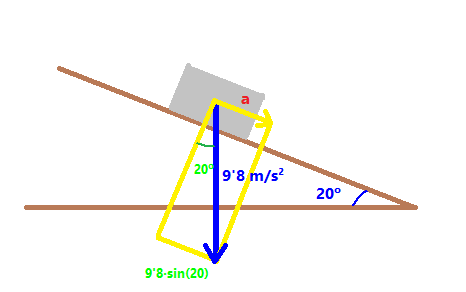 Component paral·lela al pla inclinat, a` = 9'8·sin(20)= 3'35 m/s^2` - Per moure els barcos en el canal de Panamà fan servir dues locomotores. Si l'angle entre les dues cordes és de 60º i la força que fa cada màquina és de 80 kilonewtons, quina és el módul de la força resultant (suposem la direcció de la força resultant és paral·lela al canal).  SOLUCIÓ: 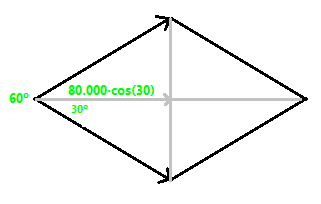 Cada màquina fa una força de `80000·cos(30)`, com hi ha dues màquines, `2·80000·cos(30) = 138564` Newtons - Anem a calcular l'altura del nostre institut.  Les eines que necessitem són: (i una taula)  Cal mesurar la distància fins la taula.   Amb quin angle veiem la part més alta de l'institut?  I cal mesurar l'altura de la taula.  Si l'angle mesurat és 32°, l'altura de la taula 80 cm. L'amplada de l'escala és de 142 cm i la mesura feta amb la cinta mètrica és de 20 metres tens totes les mesures necessàries per conèixer el que cerquem. - a) Quina distància hi ha entre el nostre institut i la punta de la muntanya de Rocacorba?  Per fer-ho només cal saber l'altitud on ens trobem.  L'altitud de la muntanya de Rocacorba:  I l'angle mesurat: (6°)  b) Pots dir la distància fins la base de la muntanya en el punt de l'antena? El google maps dóna: 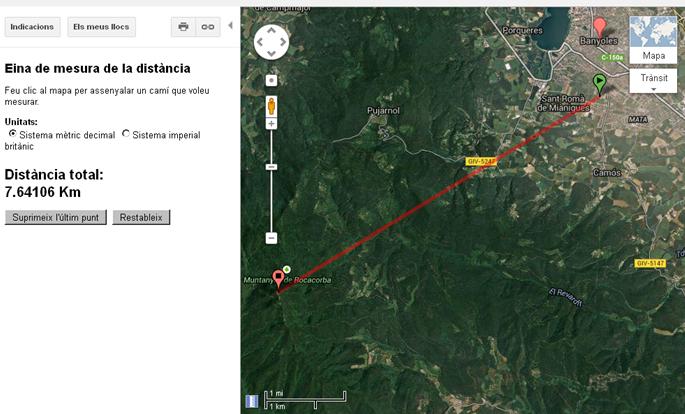 - Funcions trigonomètriques. Programa "Estudi del so en temps real". Baixar programa, OsciloEspectroScopi Àmbits: Llengües, Biologia, Psicologia, Física, Música, Informàtica, Matemàtiques. -En aquesta pràctica veiem la cadena de la parla. Des de que una persona pensa un missatge que vol transmetre fins que la persona receptora el comprèn. -A continuació es mostra el model de receptor que és el sistema Micròfon, tarja de so, ordinador. -Es mosten varis conceptes: Volum (Amplitud), to (freqüència), Timbre. Diferèncis entre la veu de nois i noies, sons sonors i sords, diferència entre els diversos fonemes (per exemple els vocàlics). Pas de la funció d'ona a l'espectre de freqüènces (funcions trigonomètriques). -Aplicacions: Telèfons, escoltar música, Siri de l'Iphone, sintetitzadors musicals, sistemes de baix cost per monitoritzar el cor durant el part que poden reduir la mortaldat neonatal, canviar la propia veu (lúdica)... 
`d(\alpha)=(v_i^2·sin(2\alpha))/g` Aquesta fórmula (D'on surt? Quin és el resultat del problema) és la nostra bola de cristall que ens permetrà saber la distància que assoleix una bala disparada per un canó inclinat un angle `\alpha` respecte l'horitzontal que surt amb una velocitat `v_i`. De moment no parlarem d'on surt aquesta fórmula tot i que conèixer la seva gènesi no només és interessant pel fet de conèixer com s'inventa (es genera) un model matemàtic, sinó perquè aquest en concret va ser el tret de sortida de la forma de fer ciència tal com l'entenem avui en dia. Model matemàtic és:
2-El millor decididor del futur per decidir què passarà. Si volem que la bala caigui en un lloc concret, la fórmula ens diu com hem de posar el canó. 3-Si hi ha coses que desconeixem, com la velocitat inicial de la bala, la fórmula ens ho dirà realitzant un experiment, un disparo. 4-Què passarà si. En funció de l'angle, fins on arriba la bala. Cal afegir, quan es fa servir un model matemàtic també cal conèixer les serves limitacions, que en aquest cas es coneixen:
 Agraïments pels dibuixos d'ARASAAC. |