|
Anterior. Siguiente. Índice Trigonometría Función seno Si calculamos el seno cada 45º (p/4) a partir de –720º (-4p) hasta 720º (4p) obtendremos la siguiente tabla: Comentario Podemos hacerlo con una calculadora, una hoja de cálculo o bien con el programa trigo.exe, en este caso como que el programa sólo nos permite calcular las relaciones trigonométricas de ángulos entre –360º y 360º recordar que para calcular un ángulo superior, por ejemplo 450º, debemos restarle 360º y obtenemos 90º, ángulo de la primera vuelta con las mismas razones trigonométricas. En el caso de querer calcular un ángulo inferior a 360º debemos añadirle esta cantidad hasta que nos quede en el intervalo –360º - 360º. Así, por ejemplo, si queremos calcular el seno de –585º le añadimos 360º y obtenemos –225º.
Ahora representamos estos valores en unos ejes de coordenadas cartesianas.
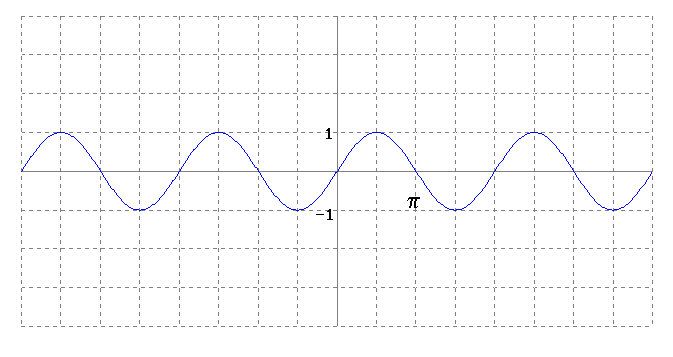
Si lo calculamos para muchos más puntos veríamos lo siguiente:
Esta forma de la gráfica es la forma de la función seno(x) que tal como vimos en la introducción tiene una forma parecida a la función de onda generada por un diapasón al ser golpeado. En realidad esto es un modelo de la evolución en función del tiempo de la elongación (distancia del punto de equilibrio respecto a la posición de reposo de las barras de diapasón). |