Cinemàtica
Sumari:
 1.
Caràcter relatiu del moviment 1.
Caràcter relatiu del moviment
Es diu que una partícula es mou quan ocupa posicions diferents
al llarg del temps. Les diferents posicions que ocupa la partícula a l'espai
es determinen mitjançant un sistema de referència. S'acostuma a agafar
com a sistema de referència un sistema cartesià d'eixos x, y, z.
Si, aquest sistema el considerem fix, el moviment resultant
de la partícula és absolut; si es mou, el moviment és relatiu. En el nostre
Cosmos, tots els moviments són relatius, ja que no existeixen punts fixos
o immòbils. Tot i això, considerem alguns sistemes fixos per convenció
que són anomenats sistemes de referència inercials.
 2.
Vector de posició 2.
Vector de posició
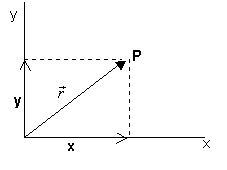
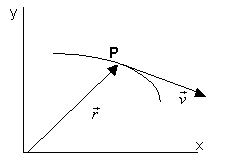
En el nostre sistema de referència, la posició de la partícula
mòbil en cada instant, queda determinada pel vector de posició , l'origen
del qual és el punt O del sistema de referència i el seu extrem, la posició
de la partícula.
Donat que la partícula es mou al llarg del temps, el vector
posició és funció del temps: 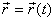 i podem escriure per aquest vector:
i podem escriure per aquest vector: 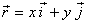 essent x e y les components del vector en una posició donada.
essent x e y les components del vector en una posició donada.
 3.
Vector desplaçament 3.
Vector desplaçament
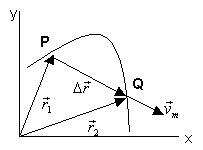
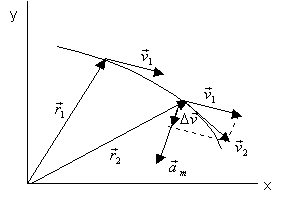
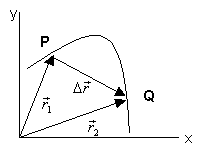 A mesura que passa el
temps, la partícula es mou i el vector de posició varia de direcció i
de mòdul.
A mesura que passa el
temps, la partícula es mou i el vector de posició varia de direcció i
de mòdul.
S'anomena vector desplaçament el vector diferència,
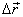 , dels vector posició final i inicial :
, dels vector posició final i inicial : 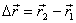
Aquest vector té origen a la posició inicial del mòbil
i extrem en la posició final.
La trajectòria d'un mòbil queda determinada per les successives
posicions que ocupa al llarg del temps.
Exercici 2:
Calculeu el vector desplaçament, del mòbil
de l'exercici 1, entre els instants 1s i 3s
(R: 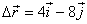 m)
m)
 4.
Vector velocitat mitjana 4.
Vector velocitat mitjana
El vector velocitat mitjana és la relació entre el vector
desplaçament i el temps emprat per realitzar-lo.
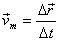
essent 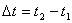
El vector
velocitat mitjana té la mateixa direcció i el mateix
sentit que el vector desplaçament.
Exercici 3:
El
moviment d'una partícula està determinat pel vector posició:
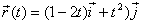 en
unitats de l’SI. Calculeu la velocitat mitjana d'aquesta partícula en l'interval de t=2s
a t=4s; Quan val el mòdul d'aquest vector? (R: 6,32
m/s) en
unitats de l’SI. Calculeu la velocitat mitjana d'aquesta partícula en l'interval de t=2s
a t=4s; Quan val el mòdul d'aquest vector? (R: 6,32
m/s)
 5.
Vector velocitat instantània 5.
Vector velocitat instantània
El vector velocitat instantània és el límit del vector velocitat
mitjana, quan l'interval de temps tendeix a zero i per tant és la derivada
del vector posició respecte del temps.
El vector velocitat instantània té la direcció de la recta
tangent a la trajectòria en el punt considerat, amb el sentit del moviment.
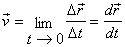
Components cartesianes
del vector velocitat
En un sistema de referència cartesià si anomenen vx,
vy, les components del vector velocitat, es pot definir aquest
vector de la següent manera: 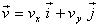 on
on
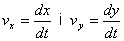
 6.
Vector acceleració 6.
Vector acceleració
L'acceleració és una mesura del canvi de la velocitat al
llarg del temps. En el Sistema Internacional es mesura en m/s2
6.1. Vector acceleració mitjana
 El vector acceleració mitjana és el
quocient entre la variació de la velocitat i el temps emprat en aquesta
variació:
El vector acceleració mitjana és el
quocient entre la variació de la velocitat i el temps emprat en aquesta
variació:
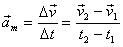
L'acceleració mitjana és un vector la direcció i el sentit
del qual depenen de les velocitats final i inicial en l'interval considerat.
6.2. Vector
acceleració instantània
El vector
acceleració instantània és el límit de l'acceleració mitjana quan Dt tendeix a zero, per tant és la derivada
del vector velocitat instantània respecte del temps:
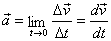
 Aquest vector expressat en components
és:
Aquest vector expressat en components
és: 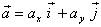 on
on
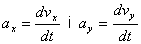
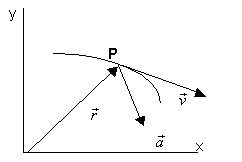
El vector acceleració instantània a cada punt de la trajectòria
té una direcció determinada i és cap a l’interior de la trajectòria.
Exercici 4:
La
posició d'un mòbil és determinada per l'equació següent: 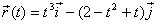 en unitats de l’SI.
en unitats de l’SI.
Determineu:
a) el vector velocitat mitjana entre t=1s i t=2s
(R: 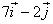 m)
m)
b) el vector
velocitat instantània a t=2s (R:
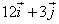 m/s)
m/s)
c) el vector
acceleració mitjana entre t=1s i t=2s (R: 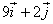 m/s2)
m/s2)
d)
el vector acceleració instantània en t=1s i en t=2s. És un moviment
uniformement accelerat?
(R: 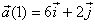 m/s2,
m/s2, 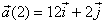 m/s2; no)
m/s2; no)
 7.
Moviment uniformement accelerat (MUA) 7.
Moviment uniformement accelerat (MUA)
En un moviment uniformement accelerat el vector acceleració
constant.
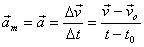
Les magnituds amb subíndex (o) indiquen els valors inicials.
Aïllant, obtenim l'equació del vector velocitat:
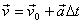
L'equació de la posició és:
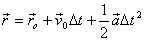
·
Moviment
en dues dimensions sota l'acció exclusiva de la gravetat
Tots els cossos que es mouen dins del camp gravitatori estan
sotmesos a l'acceleració de la gravetat. Suposant que aquesta és constant,
els cossos fan un moviment uniformement accelerat. El valor de l’acceleració
de la gravetat en la superfície terrestre és de 9,8 m/s2.
Quan la velocitat inicial del mòbil no té la direcció vertical
el cos descriu una trajectòria parabòlica i cal estudiar el moviment des
d’un sistema de referència bidimensional.
El vector acceleració és: 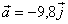 m/s2
m/s2
El moviment queda per tant descrit per les equacions del
moviment uniformement accelerat:
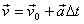
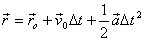
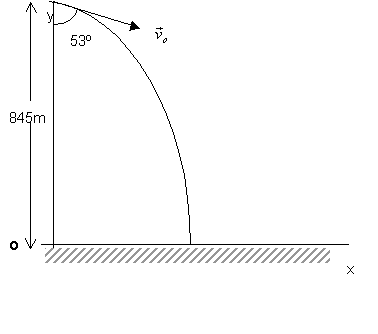
Un avió llança una bomba
a l’entrar en picat fent un angle de 53º amb la vertical, des de 845 m
d’altura. Si el projectil triga 5 s en arribar a terra, calculeu:
a)
la velocitat de l’avió en m/s
b)
la distància horitzontal de l’impacte de
la bomba a la vertical del punt de llançament
c) les components de la velocitat de la
bomba a l'arribar a terra.
Resolució:
a) L’equació del vector posició
és: 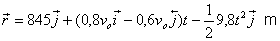
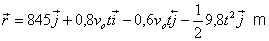
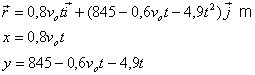
En arribar al terra t=5 s
i y=0 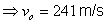
b) la distància horitzontal
de l’impacte és: x=0,8*241*.5 = 963 m
c)
el vector velocitat
és: 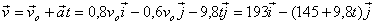
per a t=5 s 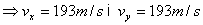
i la velocitat resultant
és: 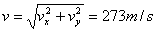
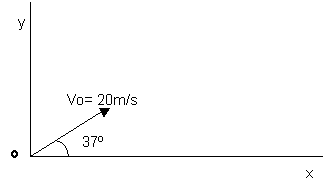 En un instant determinat les rodes posteriors d’un
camió projecten una pedreta cap endarrera. La pedra surt disparada a 72
km/h, amb un angle de 37º sobre l’horitzontal. Calculeu la màxima altura
que assoleix aquesta pedra.
En un instant determinat les rodes posteriors d’un
camió projecten una pedreta cap endarrera. La pedra surt disparada a 72
km/h, amb un angle de 37º sobre l’horitzontal. Calculeu la màxima altura
que assoleix aquesta pedra.
Resolució:

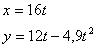
L’equació del vector velocitat
és:
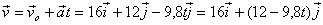
En arribar la pedra al punt
més alt el vector velocitat és horitzontal i per tant la component vertical
és nul·la, on deduïm el temps en arribar a dalt.
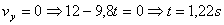
Substituint aquest temps
a la component vertical del vector posició obtenim l’altura màxima
|
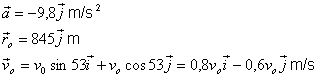
![]()
![]()
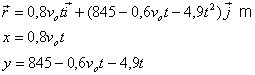
![]()
![]()
![]()
![]()
 En un instant determinat les rodes posteriors d’un
camió projecten una pedreta cap endarrera. La pedra surt disparada a 72
km/h, amb un angle de 37º sobre l’horitzontal. Calculeu la màxima altura
que assoleix aquesta pedra.
En un instant determinat les rodes posteriors d’un
camió projecten una pedreta cap endarrera. La pedra surt disparada a 72
km/h, amb un angle de 37º sobre l’horitzontal. Calculeu la màxima altura
que assoleix aquesta pedra.
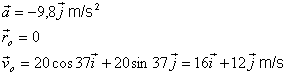 L’equació del vector posició és:
L’equació del vector posició és: ![]()
![]()
![]()
![]()
![]()
![]()