Campo eléctrico

Clicando en diferentes puntos de la pantalla podemos ver el vector campo eléctrico, o sea la fuerza eléctrica que actuaría sobre una carga de 1 C situada en este punto. Si lo hacemos con diferentes configuraciones podemos ayudar al alumno a entender el concepto de campo:

• Una única carga: ver que el campo siempre es radial y que disminuye con la distancia. Observaremos que si la carga es positiva el campo es hacia afuera y si es negativa es hacia adentro.
• Activando la cuadrícula y la opción Ajustar valores: se puede repetir el ejemplo anterior y ver que la disminución del valor del campo corresponde exactamente al inverso del cuadrado de la distancia (si la distancia se duplica, el campo disminuye en la cuarta parte).
• Dipolo: se puede mostrar el campo en algún punto de la pantalla, para ver que efectivamente correspondería a la fuerza que actuaría sobre una carga positiva (de +1 C) y que es el resultado de una suma vectorial. Concretamente puede verse que en los puntos del eje y el campo es horizontal (las componentes verticales se anulan entre ellas).
• Dos cargas de igual signo (modificación de la configuración anterior clicando en la carga): igualmente se puede mostrar el campo eléctrico en algún punto de la pantalla. Es especialmente interesante comentar cómo será el campo en los puntos del eje y. También será interesante que los alumnos realicen sus hipótesis antes de mostrar el resultado.
• Otras configuraciones más complicadas: el profesor puede incrementar el nivel de dificultad del análisis del campo eléctrico en función del nivel de los alumnos.
  

Potencial eléctrico

Clicando en diferentes puntos podemos observar el valor del potencial eléctrico (trabajo que es preciso hacer para llevar una carga de un Coulomb desde el infinito hasta este punto). Podemos entre otros...

• Recordar, y comprobar, que el potencial puede ser positivo o negativo. Será positivo si hemos de empujar la carga para transportarla des del infinito hasta el punto en cuestión.
• Repetir la secuencia de ejemplos anteriores.
• En el caso numérico, comprobar que el potencial disminuye con la distancia (pero no de forma cuadrática).
• Comprobar que campo nulo no significa potencial nulo.
• Comprobar también que si nos acercamos al infinito el potencial tiende a cero.
  

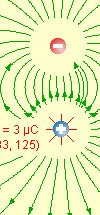
Líneas de fuerza (o de campo)

El applet dibuja bastante exactamente las líneas de fuerza. Por ello, el profesor puede utilizar esta herramienta para explicar que...

• La línea de fuerza nos da una idea no sólo del sentido del campo en cualquier punto del espacio, sino también del módulo teniendo en cuenta que la densidad de líneas está directamente relacionada con el módulo del campo eléctrico.
• Las líneas de fuerza siempre entran hacia las cargas negativas y salen de las cargas positivas.
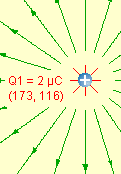
• Con una única carga las líneas son radiales.
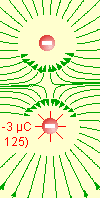
• En el caso de un dipolo las líneas salen de la carga positiva y mueren en la carga negativa.
• Si existen sólo dos cargas de igual signo, las líneas entran (o salen) en cada carga y provienen del infinito (o tienden a...).
  

Líneas equipotenciales

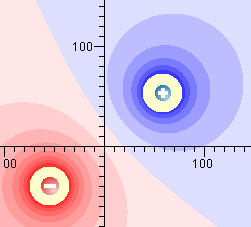
El applet dibuja toda la pantalla de color. Propiamente las líneas equipotencials serían las líneas que determinan el cambio de color.

La escala de colores (en J/C) se calcula en cada caso según la configuración de cargas, por tanto podríamos hablar con propiedad de zonas "entrepotenciales". Entre una zona (color) y la siguiente hay una diferencia de potencial constante, que también es diferente para cada configuración.

Los potenciales pueden ser positivos, color azul, o negativos, color rojo. La intensidad del color, ya sea azul o rojo, es proporcional al módulo del potencial. Estos criterios nos pueden ser de ayuda para imaginar de forma tridimensional el dibujo: las zonas azules salen de la pantalla y las rojas se hunden de modo parecido a las curvas de nivel de un plano de una zona montañosa situada cerca de la costa.

El applet, al finalizar de dibujar las líneas, dibuja la escala de colores utilizada con el correspondiente valor de potencial de cada color.

Para conocer el valor del potencial de una línea podemos clicar en un punto cualquiera de la pantalla para leer el valor del potencial eléctrico.

También podemos utilizar el dibujo para referirnos a otros aspectos como por ejemplo:

• El campo eléctrico no es constante a lo largo de una línea equipotencial.
• Que el campo sea cero no implica que el potencial sea nulo en este punto.
• Las líneas equipotenciales son parecidas a les curvas de nivel de un mapa topográfico. En lugar de representar alturas o profundidades en ralación al nivel del mar representan alturas eléctricas (potenciales eléctricos) respeto una altura cero situada en el infinito. De este modo podemos intentar imaginarnos las líneas equipotencials con relieve: las cargas negativas estarían situadas en pozos de potencial y en cambio las positivas estarían en montañas de potencial. Eso se visualiza perfectamente con la opciónEquipotenciales 3D.

No es preciso decir que es interesante mostrar los mismos ejemplos que hemos trabajado con las líneas de fuerza:

• Una sola carga: Circunferencias concéntricas.
• Un dipolo: Líneas curvas cerradas alrededor de cada carga, de potencial positivo cerca de la carga positiva y viceversa.
• Dos cargas del mismo signo: Líneas curvas cerradas pero el potencial siempre es positivo o negativo según el signo de la carga.
• Un condensador: En el interior del condensador las líneas equipotenciales son prácticamente paralelas a las placas y la diferencia de potencial se mantiene muy constante (líneas separadas regularmente).
• Una circunferencia: Tanto en el interior como en el exterior, las líneas son circunferencias concéntricas, tal y como si todas las cargas las concentrásemos en el centro (carga puntual).
  

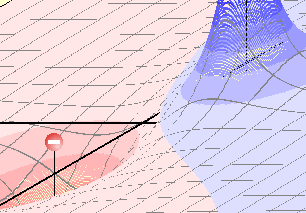
Equipotenciales 3D

Con la vista en tres dimensiones del potencial eléctrico el alumno mejorará el aprendizaje del concepto (siempre abstracto) de esta magnitud.

Por ello es importante que el profesor explique el paralelismo que hay entre el potencial eléctrico y la altura.

Cualquier objeto sabemos, por experiencia, que tiende a disminuir de altura en el campo gravitatorio. Las masas se mueven siempre hacia potenciales bajos. Podemos asociar pues el potencial eléctrico a altura.

Si existiesen masas negativas subirían en lugar de caer: si dejásemos caer un balón de masa negativa ésta aceleraría hacia lo alto (g = +9,8 m/s2). Sería una gran solución al problema del transporte!

Podemos trabajar también la relación entre el campo y el potencial (E = -grad V). Simplificando un poco, el campo es (menos) la variación del potencial, o sea el campo eléctrico es proporcional a la pendiente de la superficie 3D del potencial, siempre tiene la dirección de la máxima pendiente y el sentido hacia abajo. De este modo podemos evaluar la magnitud del campo en diferentes puntos y situaciones:

• Una carga positiva: Cuando más lejos de la carga más suave es la pendiente, por tanto el campo disminuye con la distancia. La pendiente (campo eléctrico) tiende a cero cuando la distancia se hace muy grande.
• Una carga negativa: La pendiente siempre va hacia la carga, por tanto éste es el sentido del campo.
• Dipolo: Entre las dos cargas de signo contrario la pendiente baja desde la carga positiva hasta la negativa, el campo eléctrico tiene por tanto este sentido. Es interesante observar que no hay ningún punto entre las dos cargas donde el campo sea nulo (pendiente cero).
• Dos cargas positivas: La superficie de potencial eléctrico semeja dos montañas (de alturas proporcionales a los valores de les cargas). En tal caso podemos ver que en un punto entre las dos cargas el campo eléctrico es cero, éste posición coincide justo en el "collado" entre las dos montañas, donde la pendiente es horizontal. También es interesante observar que este punto es más próximo a la carga de valor más pequeño.
  

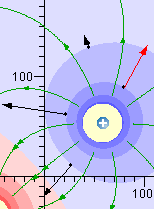
Relación entre las líneas de fuerza y las equipotencials

Es importante tener presente que podemos dibujar simultáneamente las líneas equipotenciales y/o las líneas de fuerza y/o el vector campo eléctrico de diferentes puntos. De este modo podemos comprobar gráficamente la relación que hay entre las líneas equipotenciales y las líneas de fuerza.

Teniendo en cuenta que el campo eléctrico es igual al gradiente del potencial eléctrico pero cambiado de signo, podemos comprobar que:

• Las líneas equipotenciales siempre son perpendiculares a las líneas de fuerza.
• El campo eléctrico siempre va en la dirección de máxima variación (negativa) del potencial.
• El sentido del campo es el de la disminución del potencial.
• La intensidad del campo es proporcional a la variación de potencial con el espacio (el campo eléctrico es más intenso en las zonas donde las líneas equipotenciales están más juntas).