
Ejecuta
el applet
El
profesor en el aula, con el proyector de vídeo, puede utilizar
éste applet para reforzar algunos de los conceptos sobre ondas.
De forma orientativa...
Generales
- Los frentes de ondas circulares (crestas negras y valles grises). Sin las líneas nodales ni las constructivas podemos observar como evolucionan las ondas a lo largo del tiempo. También podemos visualizarlas en la parte inferior del applet.
- Significado de la longitud de onda, modificando su valor podemos observar como varía la respresentación en el applet.
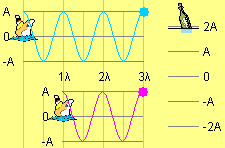
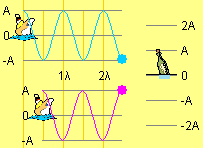
- Interferencia constructiva: situamos la botella encima de una superposición cresta-cresta y observamos en la parte inferior que la botella se encuentra en una doble amplitud. Si situamos la botella encima de un valle-valle podemos comprobar que esta se encuentra en un doble valle.
- Interferencia destructiva (nodo). Como antes situamos la botella en diferentes puntos cresta-valle para ver que la posición de la botella siempre es cero.
- Diferencia de trayecto: en la
parte inferior veremos que si la diferencia corresponde a un numero
entero de longitudes de onda nos encontramos en un punto de interferencia
constructiva. Si, en cambio, nos situamos en un punto donde la diferencia
corresponde a un número impar de semilongitudes de onda entonces
nos encontramos en un nodo (o línea nodal).
Líneas
- Líneas nodales. Antes de visualizarlas podemos intentar dibujarlas manualmente poniendo la botella sucesivamente en diferentes puntos cresta-valle. Acabaremos mostrando las líneas de color verde (activando el cuadro correspondiente). En este momento podemos comentar la existencia de varias líneas en función de las diferencias de caminos a los focos y la longitud de onda (ver la parte inferior del applet).
- Líneas de interferencia constructiva. Podemos repetir el procedimiento anterior pero ahora con las crestas-crestas o los valles-valles. Comentar que en el eje de simetría lógicamente hay una línea de interferencia constructiva.
- Número de líneas nodales. Podemos comprobar que el número de líneas varía según la longitud de onda y la distancia entre los focos. N = d (f1,f2) / lambda
Movimiento
- Movimiento de la botella encima de una interferencia constructiva. Si animamos el applet, en la parte inferior veremos que la botella oscila con una amplitud 2A.
- Con la botella encima de un nodo,
y el applet en funcionamiento, podemos comprobar que su oscilación
es nula.
Procedimientos
También podemos utilizar el applet para trabajar procedimientos y/o comprobar los resultados obtenidos en la resolución numérica de ejercicios. Podemos calcular por ejemplo:
- Dada una posición encima del plano, calcular si nos encontramos encima de un nodo.
- Calcular la posición de un punto cualquiera pero situado encima de una determinada línea nodal (o de interferencia constructiva).
- Encontrar la amplitud de la oscilación en un punto determinado
del plano.