Dos vectors amb la mateixa direcció direm que són
paral·lels, independentment de que tinguin igual
o diferent sentit, o igual o diferent mòdul. Si
agafem dos vectors 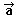 i
i 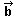 amb la
mateixa direcció, per tant paral·lels, i els
situem amb el mateix origen, veiem que podem passar d'un a
l'altre multiplicant per un escalar, és a dir, amb la
mateixa direcció, per tant paral·lels, i els
situem amb el mateix origen, veiem que podem passar d'un a
l'altre multiplicant per un escalar, és a dir,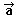 =
k =
k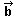 o o 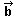 =
k' =
k'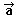 . Recíprocament,
si . Recíprocament,
si 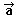 = k = k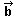 o
o 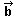 = k' = k'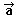 ,
els dos vectors tenen la mateixa direcció i són
paral·lels. Per tant, la condició de paral·lelisme
de vectors és que es verifiqui: ,
els dos vectors tenen la mateixa direcció i són
paral·lels. Per tant, la condició de paral·lelisme
de vectors és que es verifiqui:
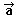 =
k =
k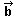 o o 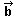 =
k' =
k'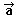
Observem que els escalars k i k' són inversos un de
l'altre.
Si els components de 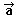 i
i 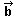 són són
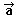 =(a1,a2)
i =(a1,a2)
i 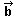 =(b1,b2),
aleshores la condició de paral·lelisme és: =(b1,b2),
aleshores la condició de paral·lelisme és:
|
(a1,a2)=k(b1,b2)
és a dir:
a1=kb1
a2=kb2
aïllant la k
de les dues igualtats anteriors i igualant el resultat, s'obté
la condició de paral·lelisme de dos vectors donats
pels seus components:
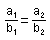
és a dir, els components han de ser proporcionals.
|
|
|
ACTIVITAT INTERACTIVA
Quins dels següents parells
de vectors
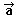 =(a1,a2)
i =(a1,a2)
i 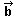 =(b1,b2)
són paral·lels entre ells? =(b1,b2)
són paral·lels entre ells?
Mira si es verifica la
condició de paral·lelisme
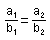
i comprova el resultat a l'applet de la dreta.
a)
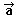 =(3,-2)
i =(3,-2)
i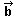 =(3,-3) =(3,-3)
b)
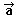 =(4,2)
i =(4,2)
i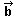 =(6,3) =(6,3)
c)
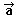 =(-3,4)
i =(-3,4)
i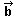 =(9,-12) =(9,-12)
d)
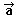 =(-2,-4)
i =(-2,-4)
i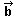 =(3,7) =(3,7)
SOLUCIÓ
|
|
|