|
"La matemática es esa extraña cosa que, incomprensiblemente, hace que el mundo sea comprensible" Què hi ha aquí?
Donada una funció `f(x)` definim Domini com el subconjunt dels nombres Reals (de l'eix `x`) que tenen imatge. El Recorregut és el subconjunt dels nombres reals (eix `y`) que són imatge. Veiem un parell d'exemples. `f(x)=x^2-4x+3`. 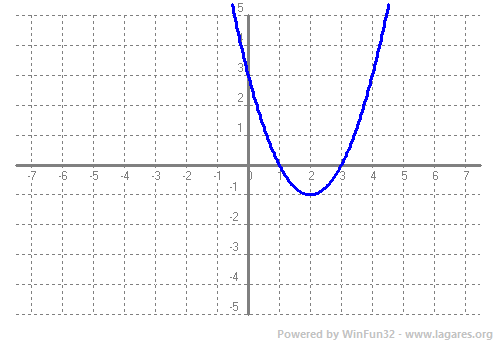 El domini de qualsevol polinomi són tots els Reals, `R`. I el recorregut, tal com podem veure a la gràfica, `[-1,+\infty)`. 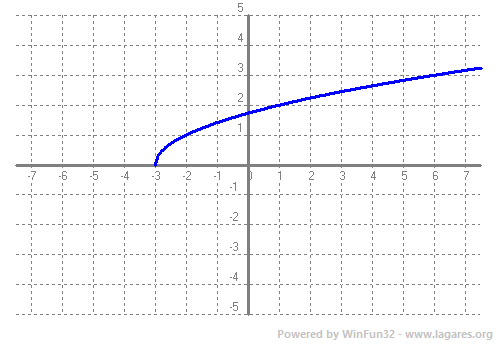 Per calcular el domini d'una arrel quadrada el que hem de fer és demanar que el que hi hagi a dins sigui `>=0` ja que les arrels de nmombres negatius no existeixen en el conjunt de nombres reals. Recordem que estem estudiant funcions Reals de variable Real. Això vol dir que els vaors tant l'eix `x`, com l'eix `y`, són nombres reals. `x+3>=0 => x>=-3`, per la qual cosa el domini de la funció `f(x)=sqrt(x+3)` és, `[-3,+\infty)`. Que de fet, es pot veure directament a la gràfica. El recorregut, mirant-ho a la gràfica, `[0,+\infty)`. En general el recorregut el trobarem en la gràfica, però el domini farem servir les propietats de les funcions. Així si tenim un quocient, cal recordar que no pot ser `0`. `f(x)=1/x`, domini `R-{0}`. 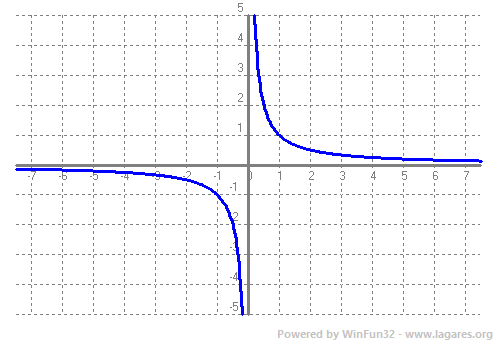 Si tenim una arrel d'index parell, cal recordar que està definida per nombres `x>=0`. 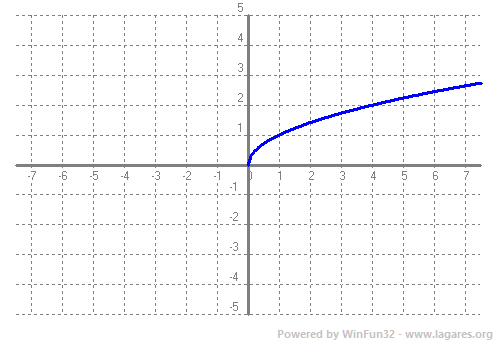 La funció exponencial, `e^x`, està definida per tots els reals. 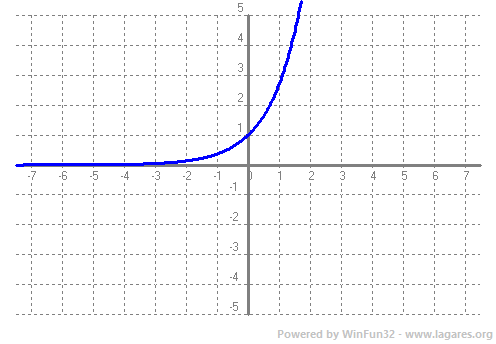 La función `ln(x)` pels nombres positius, `x>0`. 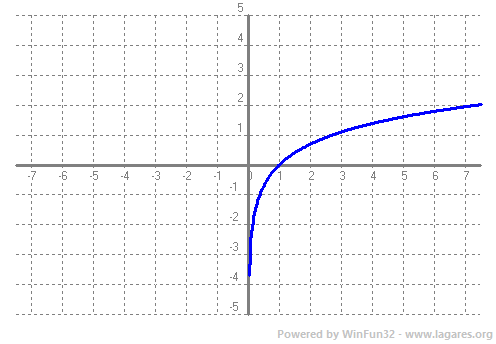 Les funcions `sin(x)` i `cos(x)` estan definides per tots els reals. 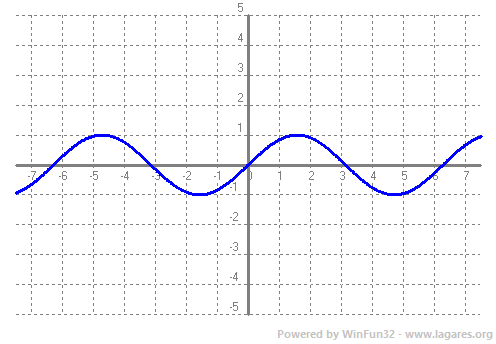 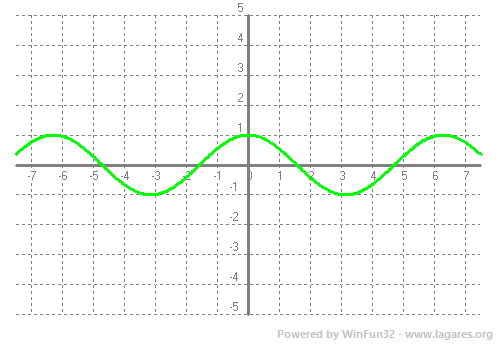 I la funció `tan(x)`, per a tots els reals excepte la familia de 90º i 180º, Domini de `tan(x)= R - {90+180k} k \in Z`... 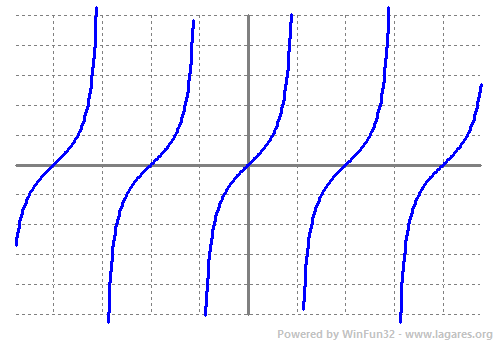
Donades dues funcions, per exemple, `f(x)=x` i `g(x)=sin(x)` podem definir noves funcions a partir de fer operacions amb elles. Així podem definir: La suma, `+`, `(f+g)(x)=x+sin(x)` 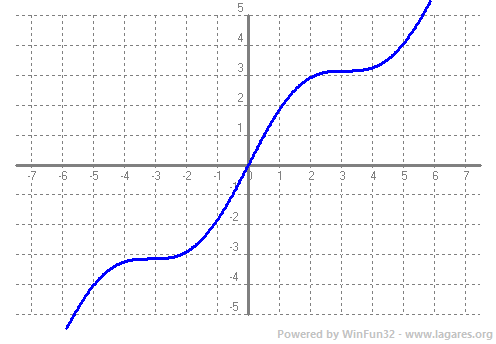 La diferència, `-`, `(f-g)(x)=x-sin(x)` 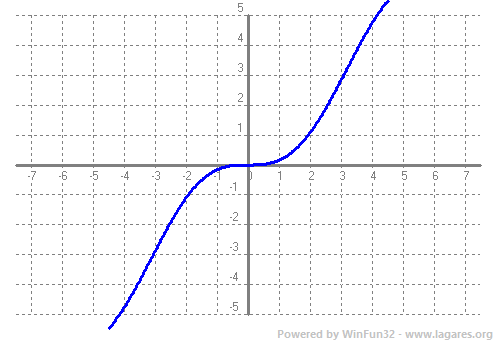 El producte, `·`, `(f·g)(x)=x·sin(x)` 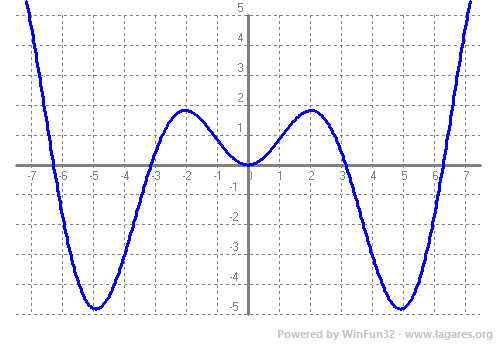 El quocient (o divisió), `/`, `(g/f)(x)=(sin(x))/x` 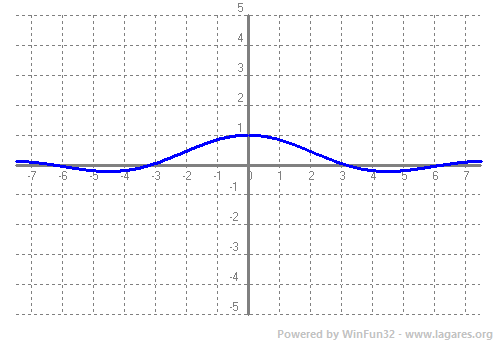 O sigui, a partir de les funcions senzilles que coneixem (funcions elementals), podem construir noves funcions fent operacions amb elles. I quin sentit pot tenir això? Si recordes del tema de trigonometria, podiem explicar les pulsacions (dues notes lleugerament desafinades), en vam parlar en el tema de trigonometria, les podiem explicar com el producte de dues funcions `p(x)=sin(x)·sin(15x)` 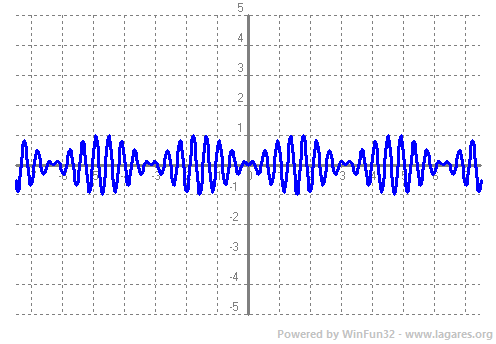 I un altre exemple, podem explicar l'atenuació d'un so com el producte d'una exponencial negativa per un sinus, `a(x)=e^(-x)·sin(x)` 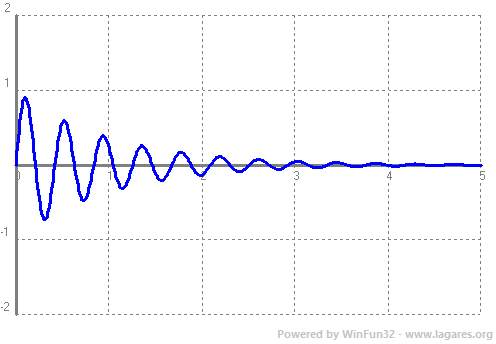 Per sintetitzar aquest so, es fa servir la fórmula següent. No només hi ha producte de funcions, també hi ha composició de funcions simples. És el que expliquem en el següent apartat.  Mireu la funció `F(x)=e^(x^2)`, és la expressió (sense certes constants de normalització) de la famosa densitat de probabilitat de la distribució normal. Ara no té massa importància el que significa, lúnic que heu de saber és que és una funció molt important, la famosa campana de Gauss. 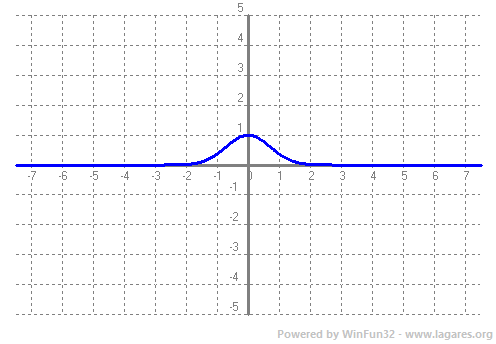 Si us hi fixeu aquesta funció no és ni cap suma, ni cap diferència, ni producte ni quocient de funcions. Aquí el que hi ha és una composició de funcions. Què vol dir això. Per calcular al imatge de un numero, per exemple el `5`, ho hem de fer en dues passes, primer cal calcular `5^2` i el que surt, `25`, a continuació hem de calcular la exponencial, `e^25`. L'important a tenir en compte quan composem dues funcions, és veure quines funcions composem i en quin ordre. Així en aquest cas la primera funció és, `g(x)=x^2` i la segona és, `f(x)=e^x`. La composició la simbolitzem, `(fog)(x)` o bé `f(g(x))`. Que en le nostre cas seria, `f(g(x))=e^(x^2)`. Un altre exemple, la funció `H(x)=ln(sqrt(x))`, aquí composem dues funcions, `g(x)=sqrt(x)` i `f(x)=ln(x)`, de la següent manera, `f(g(x))=ln(sqrt(x))`. Fixeu-vos que si les composessim en l'ordre invers, quedaria una funció molt diferent, `g(f(x))=sqrt(ln(x))`. Suposo que sabeu que si us compreu un terreny, per exemple, quadrat de `20 m` de costat i voleu saber el preu, cal saber la seva superfície. Per fer-ho tots sabeu que la funció, `f(x)=x^2` us permet calcular l'àrea. Però què passaria si ja teniu el terreny comprat i hi voleu fer una valla, per la qual cosa necessiteu saber el seu perímetre. Però en primer lloc un costat. Com podem saber quant mesura el costat, suposem que no tenim una cintà mètrica per fer-ho. Doncs bé, si tenim l'àrea, podem saber el costat senzillament amb, la funció inversa, `f(x)=sqrt(x)`. Si feu l'arrel quadrada de la superfície obtindreu el que mesura el costat. Matemàticament que és la funció inversa? Fixeu-vos en l'exemple anterior. Teniem un costat `20` l'hem elevat al quadrat, `20^2=400`, i hem obtingut la superfície. Si a la superfície li fem l'arrel quadrada, `sqrt(400)=20`, obtenim de no el costat. Ho sigui hem tornat al principi. Si t'hi fixes veuràs que el que hem fet és una composició de funcions. Si `f(x)=sqrt(x)` i `g(x)=x^2` `=>` `f(g(x))=f(x^2)= sqrt(x^2)=x`. El resultat és el mateix d'on hem començat, `f(g(x))=x`. Quan tenim dues funcions que al composar-les, dona la funció, `x`, diem que les dues funcions són una inversa de l'altra. Si ho fas al revés dona el mateix resultat,  Les funcions inverses no són una cosa nova per nosaltres. Podeu recordar de trigonometria que la calculadora ens permet calcular, per exemple, donat un angel, el seu sinus. Però si premem la tecla, shift, prèviament, donat un sinus ens retorna el angle corresponent. Aquest nova función l'anomenàvem `arcsin`. `arcsin(sin(x))=x`. Com es fa per trobar la funió inversa? Hi ha alguns casos que són inmediats. Exemples.
`f(x)=sin(x), f^(-1)=arcsin(x)` `f(x)=cos(x), f^(-1)=arccos(x)` `f(x)=tan(x), f^(-1)=arctan(x)` `f(x)=e^x, f^(-1)=ln(x)` En altres casos, es pot intentar fer servir el següent truc. S'intercanvia la `x` per la `y` i al revés. A continuació s'aïlla la, `y`, i si es pot fer, el resulta és la funció inversa. Per exemple:
`x=(y+3)/(y-1)` `x·(y-1)=(y+3)` `xy-x=y+3` `xy-y=x+3` `(x-1)y=x+3` `y=(x+3)/(x-1)` Per comprovar que està bé, el que cal és composar les dues funcions i veure que dona, `x`. La funció identitat.
Les funcions ens mostrem com evoluciona una cosa que depèn d'un altre. Però, també, tenen una propietat poderosa, si d'un problema sabem extreure'm la funció que el modelitza, en podem treure conclusions poderoses. Per mostrar el que volem dir, ho farem amb un exemple. "Un ejemplo vale més que mil palabras". Exemple - Amb `200` metres de tanca volem delimitar un recinte rectangular aprofitant una paret molt llarga. a) Construeix la funció que dóna l'àrea a partir de la longitud d'un dels dos costats. b) Digues quin és el domini. c) Quines dimensions ha de tenir la tanca perquè l'àrea engabiada sigui máxima? SOLUCIÓ.
Al grà: Fent un dibuix de la situació, ens pot ajudar a plantejar-la. Cal, també, saber decidir qui és la incògnita que no és més que la variable independent la funció, `x`. No ´s obligatori fer servir aquesta lletra.  a) Si en diem `x` al que mesura cadasun dels dos costats verticals, el costat horitzontal mesura, `200-2x`, ja que entre tots tres mesures `200` metres. Recordeu que la tanca només s'ha de fer servir en tres costats ja que l'altra costat no necesitem tanca, ja que hi ha la pared. Per trobar l'àrea només cal calcular l'àrea d'un rectangle. b) Si us fixeu amb la fórmula que ens ha quedat veiem que és una funció de segon grau. A més com l'`a=-2>0 =>` que la gràfica és una paràbola amb les banyes cap avall. O sigui el vèrtex serà un màxim (que ens va molt bé, ja que serà la resposta a la pregunta `c`, que és l'objectiu que busca el problema. Per la qual cosa, per trobar el domini només haurem de trobar els punt. de tall amb l'eix de les `x`. Recordem que l'única que hem de fer és igualar la funció a `0` i resoldre l'equació resultant. O sigui, el domini són els números que hi ha entre `(0,100)`. Posem interval obert ja que un rectangle den que una dimensió vol `0` no té gaire sentit com a rectangle. c) Amb el que hem dit abans trobar les dimensions del rectangle que fan que l'àra sigui màxima sigui bufar i fer ampolles. Trobem el vèrtex de la paràbola, `x_c=(-b)/(2a)=(-200)/(2·(-2))=50`. O sigui, el costat, vertical, ha de mesurar, `50` metres i l'horitzontal, `200-2x=200-2·50=100` metres.  Hi ha una dada que el problema no demana, però és interessant coneixer-la. Quan mesura l'àrea? `A(x)=-2x^2+200x => A(50)=-2·50^2+200·50 = 5000 m^2`. No és rellevant per el problema, però pot ajudara entendre el que ha pssat si representem la funció que realciona l'àrea en funció de la longitud vertical de la tanca (lo de vertical es refereix al dibuix). 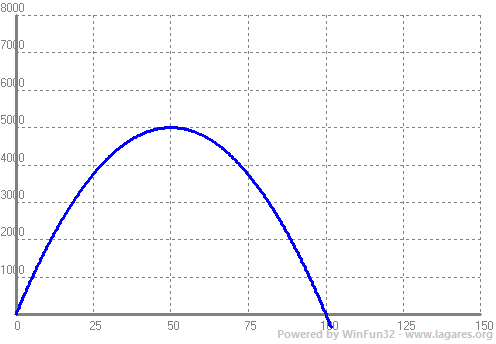 Encara volia fer una altra reflexió sobre el problema. Acabem de dir que és molt interessant saber optimitzar funcions, trobar màixim i/o mínims, i en aquest cas ha sigut fàcil trobar-lo, ja que es tractava d'una funció de segon grau que coneixem el seu comportament. Té un màxim (o mínim) que és el vèrtex. I sabem calcular on és, `x_v=(-b)/(2a)`. De seguida ens ha de venir al cap la pregunta, i si la funció no és de segon grau, com ho fem per optimitza-la si no és de segon grau? La resposta serà trobar els punts on la derivada val `0`, tal com varem explicar al princiì del tema, però per saber com es fa i com funciona això, ho deixarem per més endavant. Aquí la idea és que agafeu ganes d'aprendre-ho, ja que el fet de que nels avion volin i els ponts no caiguin ;-) depenen d'això. 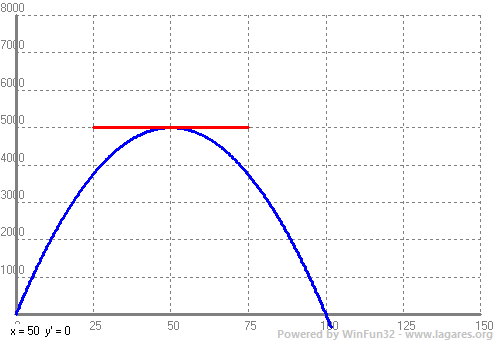 |