|
"La matemática es esa extraña cosa que, incomprensiblemente, hace que el mundo sea comprensible" Una successió és creixent si cada terme és més gran que l'anterior `a_(n+1) > a_n`. Una successió és decreixent si cada terme és més petit que l'anterior `a_(n+1) < a_n`. Les successions que o són creixents o són decreixents, s'anomenen monòtones. Una successió està fitada si hi ha números (no cal que siguin de la successió) que siguin més grans (o iguals) que tots els termes de la successió i altres números que siguin més petits (o iguals) que tots els termes de la successió. Així: `a_n = n^2 = {1, 4, 9, 16,...}` és creixent i clàrament no fitada perquè qualsevol nombre que penseu arribarà un moment que hi haurà un terme de la successió que serà més gran. per exemple si pensem `1000000`, el terme `a_1001 = 1001^2` és més gran que 1000000. `b_n = 1/n = {1, 1/2, 1/3, 1/4, ...}` és decreixent i fitada perquè `2` és més gran que tots els termes de la successió i `-1` és més petit que qualsevol terme de la successió ja que aquesta mai pot ser negativa. `C_n = (-1)^n = {-1, 1, -1, 1, -1, 1, ...}` no és ni creixent, ni decreixent (no és monótona), però sí que està fitada ja que `2` és una fita superior (més gran que tots els termes de la successió) i `-2` és una fita inferior. `D_n = (-2)^n = {-2, 4, -8, 16, -32, 64, -128, ... }` no és ni creixent, ni decreixent. tampoc està fitada ni per sobre (superiorment), ni per sota (inferiorment). Per ajudar a entendre tot plegat partirem d'unes dades molt properes. La taula següent mostra la successió dels nombres de casos de persones que detectades amb la malaltia de coronavirus en funció del dia. 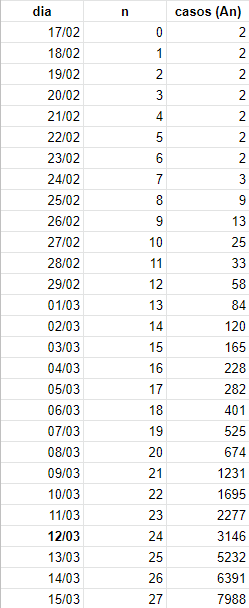 El dia 12 és el dia que es va tancar l'institut. Si representem en uns eixos de coordenades aquest valors obtenim: 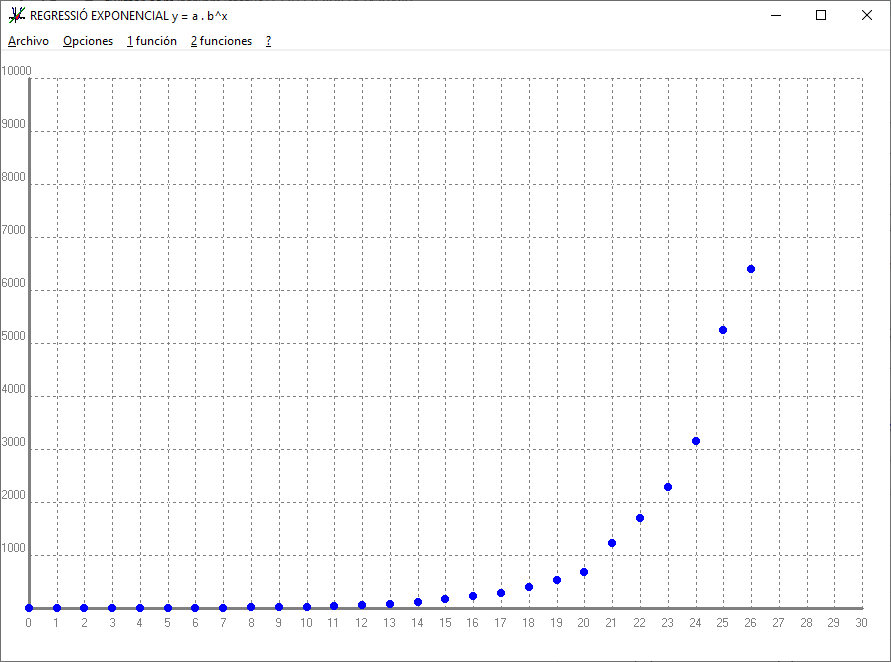 Observem que la successió és clarament creixent. Aquestes successió de dades es poden ajustar, desgraciadament, amb una fórmula anomenada, regressió exponencial, amb el següent terme general: Per veure-ho, mostrarem el dibuix de la gràfica: 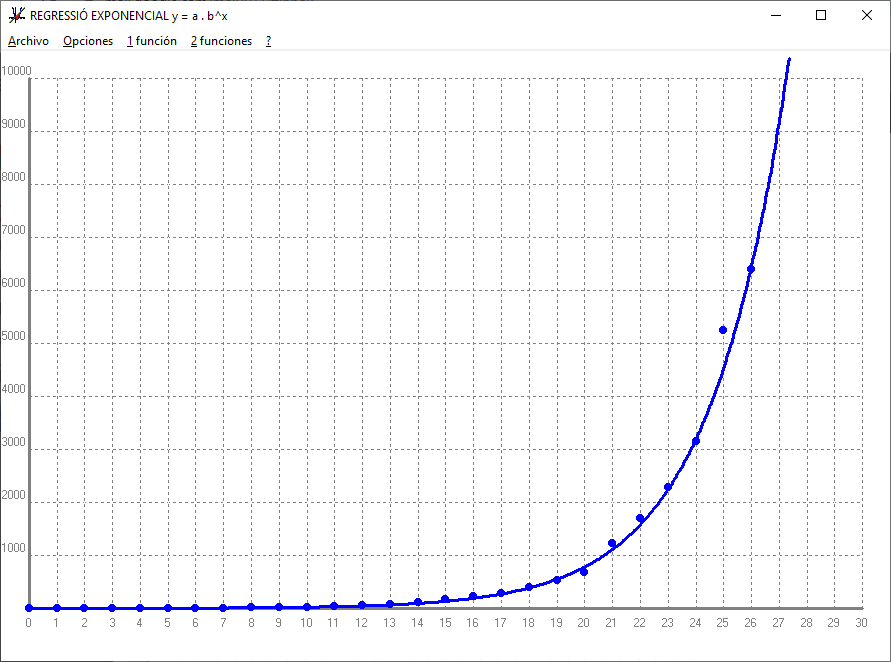 Però resulta que també aquestes dades s'ajusten molt bé amb un terme general d'una equació molt diferent. Aquesta equació rep el nom de funció sigmoidea i és molt important en l'àmbit de machine learning i deep learning (Intel·ligència artificial), però ho deixarem per una altra ocasió. Si representem les dues gràfiques juntes observem el que he dit, que les dues fórmules ajusten prou bé. Blava `a_n` i verda `b_n`. 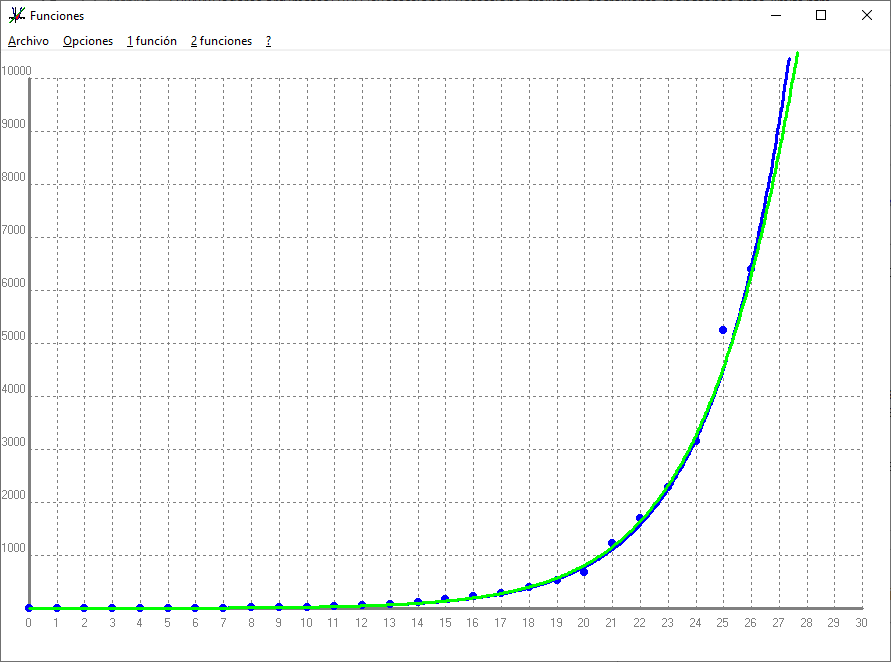 Què passa, però, si mirem més tros de les dues gràfiques? Canviem els valors dels eixos de coordenades: 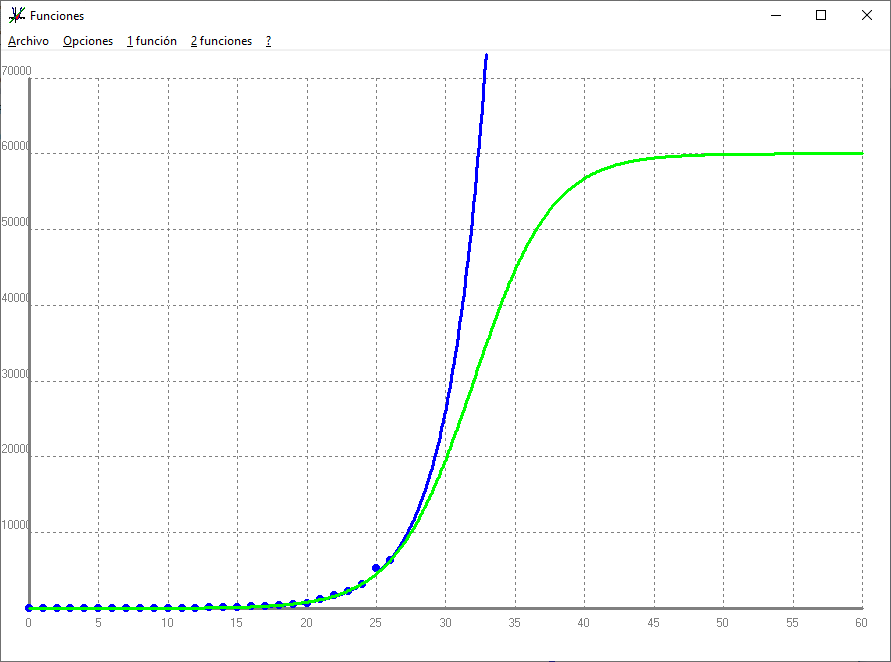 Veiem que el comportament de les dues gràfiques és molt diferent. Quin dels dos comportaments voldríem que seguís a partir d'ara el nombre de persones afectades de coronavirus a Espanya? La primera successió, `a_n = 0,685753 · 1,421701^n` ,veiem que és creixent i cada vegada creix més i no està fitada. La segona, `b_n = 60000/(1+e^((32-n)/(2,8)))`, veiem que que sí està fitada, ja que mai serà més gran que `70000`. La successió `a_n` el seu límit és `+\infty`. La successió `b_n` el seu límit és `60000`. Espero que hagi quedat clar el concepte, i la importància, de saber calcular límits, per la qual cosa a continuació aprendrem a fer-ho. 1-Límits de polinomis: `b_n = 4n^2-100n-1000` Donaran `+\infty` o `-\infty` segons el signe del quoeficient del monomi de major grau o sigui: `lim (-3n^3+4n^2+6n-3) = -\infty` i `lim (4n^2-100n-1000) = \infty` ja que en el primer cas el quoeficient del monomi de major grau `-3n^3` és `-3` i és negatiu i en el segon cas el quoeficient del monomi de major grau `4n^3` és `4` i és positiu. El perquè d'això és senzill justificar-ho perquè si penses en el terme 10000 de la segona successió, el segon milio és molt més petit que el 400000000 primer. Si a sobre busquessis el terme n_1000000 o més gran la tendència cap a `+\infty` és molt més gran. 2-Límits de fraccions algebraiques. Quocients de polinomis:
Que el grau del polinomi de dalt sigui més gran que el grau del polinomi de baix: Que el grau del polinomi de dalt sigui més petit que el grau del polinomi de baix: Que els graus dels dos polinomis siguin iguals: Fent servir un raonament anàleg a lo de dalt podem veure que: `a_n`. Que el grau del polinomi de dalt sigui més gran que el grau del polinomi de baix, el limit pot ser, `+\infty` i `-\infty`. El que determina el signe és el quocient dels signes dels quoeficients dels monomis de major grau. En aquest cas és `-\infty` perquè el signe de `-3/1 = -` `b_n`. Que el grau del polinomi de dalt sigui més petit que el grau del polinomi de baix, el límit és `0` `c_n`. I en el cas de que els graus dels dos polinomis siguin iguals, si calculem termes cada vegada més grans `c_100`, `c_10000000`, observaràs que el límit tendeix al quocient dels quoeficients dels polinomis de major grau, `(3n^4)/(-5n^4)=3/(-5)` 3-Límits de diferències:
Si calculem el límit independentment per cada fracció, podem pensar que és `+\infty -\infty` i que dona `0`, però si mirem aquets dos exemples ja veiem de seguida que `+\infty -\infty` pot donar resultats diferents. lim `n^2-n^3 = +\infty -\infty` i en un apartat anterior (límits de polinomis) hem vist que dona `-\infty` i si ho fem al revés lim `n^3-n^2 = +\infty` Sempre que ens trobem en un cas semblant com, `+\infty -\infty`, que pugui donar resultats diferents direm que el límit (de bones a primeres) és indeterminat. I calcular el límit serà treure la indeterminació, és a dir descobrir realment quin és el límit. Per fer-ho, practicament amb exemples. Calculem el límit de la successió proposada. Per fer-ho cal fer la operació de la resta de fraccions. Això ja en sabem des de primàrica, comú denominador, etc. `a_n=(n^2+2)/n-(n^2-2)/(n+1)=` `((n^2+2)·(n+1))/(n(n+1))-(n.(n^2-2))/(n(n+1)) =` `(n^3+n^2+2n+2)/(n^2+n)-(n^3-2n)/(n^2+n) =` `((n^3+n^2+2n+2)-(n^3-2n))/(n^2+n) =` `(n^3+n^2+2n+2-n^3+2n)/(n^2+n) =` Evidenment hem fet servir el criteri per calcular límits d'un quocient de polinomis. Anem per l'exemple on surtin arrels: Tornem a tenir un `+\infty -\infty`, en aquests casos per calcular el límit multipliquem i dividim pel conjugat. recordeu que el conjugat d'un `-` és una `-` i viceversa. `lim((sqrt(n^2-n)-n) ·(sqrt(n^2-n)+n))/(sqrt(n^2-n)+n) =` Com tenim una diferència per una suma és diferència de quadrats marxem, a dalt les arrels. `lim((n^2-n)-n^2)/(sqrt(n^2-n)+n) =` `lim(n^2-n-n^2)/(sqrt(n^2-n)+n) =` `lim(-n)/(sqrt(n^2-n)+n)` Aquí cal mirar graus. A dalt és clàrament grau `-1`. A baix `sqrt(n^2)` és grau `1`, com el coeficient és `1`, el coeficient del monomi de grau `1` és `sqrt(1)+1 = 2`. De grau 1 també hi ha l'`n` de la dreta, `(sqrt(n^2-n)+n)`. Resumint, els grau del numerador és `1`, el del denominador també, `1`. Quan tenim el mateix grau als dos llocs, cal dividir els coeficients. Un exemple més per ajudar a entendre això: Per calcular aquest límit procedirem com si fos un quocient de polinomis. El monomi de grau més gran del numerador és: `root(3){2n^4}`. Grau `4/3`, recordeu `root(3){2n^4}= (2n)^(4/3)`, i el coeficient serà `root(3){2}` El monomi de grau més gran del denominador és, `root(6){3n^8}`. El grau és, `8/6=4/3`, que és el mateix que el numerador. Per la qual cosa el límit serà el quocient dels coeficients, que en el cas del denominador és, `root(6){3}`. 4-Límits de potències:
L'única que hem de fer és calcular el límit de la base i el límit de l'exponent. En aquest cas, ja que tan a la base com l'exponent són quocients de polinomis, tots amb el mateix grau: Però la cosa no sempre serà tan senzilla, aquí poden sortir `0, 1, \infty` que veurem que per calcular-los haurem de treballar una mica. Com sempre veurem exemples: `lim 3^n` això és `3^(+\infty)` i un nombre més gran que `1` elevat a una cosa cada vegada més gran evidetnment se'n va a `+\infty`. `lim (1/2)^n` això és `(1/2)^(+\infty)` i un nombre més petit que `1`, (`1/2=0'5<1`), elevat a una cosa cada vegada més gran, evidenment se'n va a `0`. Ja que `0'5^2 = 0'25, 0'5^10=0,000977, ...`. Compte en coses com `(-2)^n` que això no té límit ja que `{-2, 4, -8, 16, -32,...}`. Aquesta successió no té límit. En resum, per calcular límits de potències heu de calcular el límit de la base (b), el límit de l'exponent (p). El límit serà calcular `b^p`. Això ens servirà per al majoria dels casos. Però hi ha casos tel tipus `0^0, \infty^0, 1^\infty,` que són indeterminats, vol dir que poden donar diferents solucions. Però això ho deixem per més endavant. 5-Límits `1^\infty`. Número `e`
`1` és la base de tot plegat. És la base del comptar. `0` és un número que es va inventar relativament tard, quantifica l'absència d'alguan cosa. `\pi` és la relació que hi ha entre el perímetre i el diàmetre d'un cercle `(perímetre)/(diàmetre)`. `i` és un nombre que hem descobert aquest any i el definim com `i=sqrt(-1)`. El número `e` és el número que en volem parlar a partir d'ara. A sobre tots aquest números estan relacionats per la fórmula més important de les matemàtiques, amb permís del teorema de Pitàgores, ;-). No volem parlar d'aquesta fórmula, però sí el número `e` i, sobretot de la seva relació, millor dit, el seu origen en les successions. Us en recordeu d'aquesta fórmula? És la fórmula de l'interès compost. Aqui la `i` no és el número imaginari, `i=r/100`, on `r` és el rèdit, el % que ens dona el banc. Així, si posem `10000€` al `5%` anual la Fórmula que ens dona el capital final en funció del temps és: Ar el que m'agradaria que ens fixéssim és què passaria si invertíssim `1€` al`100%` de rèdit anual, al cap d'un any? Evidentment el Capital final serà `2` ja que si ens donen un `100%` al cap d'un any el capital es dobla. Però ara ens farem la pregunta de què passaria si jo al cap de mig any vaig a recollir els meus diners juntament amb els interessos i els torno a invertir amb les mateixes condicions. Evidentment si el tracte era del `100%` anual i els vaig a buscar al cap de mig any, m'han de donar la meitat de deiners, per la qual cosa la `i=1/2` i com deixo al banc durant `2` períodes de mig any (`1` anys = `2` mig any). La fórmula quedarà: Fixeu-vos que no cal que posem l'`1`. I el que també vull que us fixeu és que el treball d'anar al banc `2` cops en lloc de només anar-hi `1` al final ha siguit rentable, ja que hem guanyat més diners, `2'25€` en lloc de `2`. Però nosaltres, que sóm molt intel·ligents, i sobretot treballadors, decidim anar al banc un cop al més, `12` vegades. I què passaria si hi anés cada dia? Ara podriem preguntar-nos, i si hi anem cada segon? cada mil·lèssima de segon? I si féssim el límit quan el nombre de vegades que vaig al banc durant `1` any tendís a `\infinit`?. 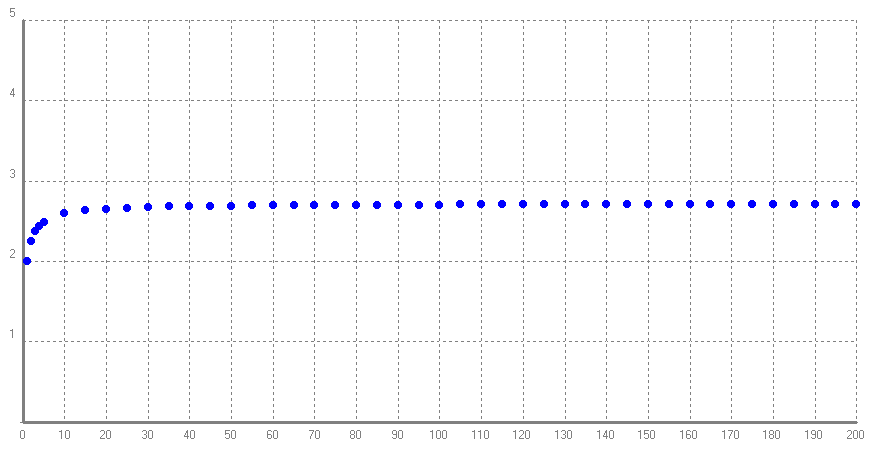 Com veieu a la gràfica, i es pot demostrar, això no puja infefinidament. Aquesta successió té límit i el límit d'aquesta successió, que és un número irracional (sense demotració), n'hi diem, número `e`. Definició de número `e` I amb poques xifres decimals, `e=2,718282`. Bé si voleu demostrar que realment aquesta successió té límit, o sigui, que el número e existeix realment cliqueu. Fixeu-vos que perquè el límit valgui `e` no cal que sigui `n` el que hi ha en el denominador i el l'exponent, metre sigui una cosa igual i que tendeixi a `+\infty` tota aquesta mena de successions tendiran al número `e`. Així per exemple veiem uns quants termes de les successions següents:
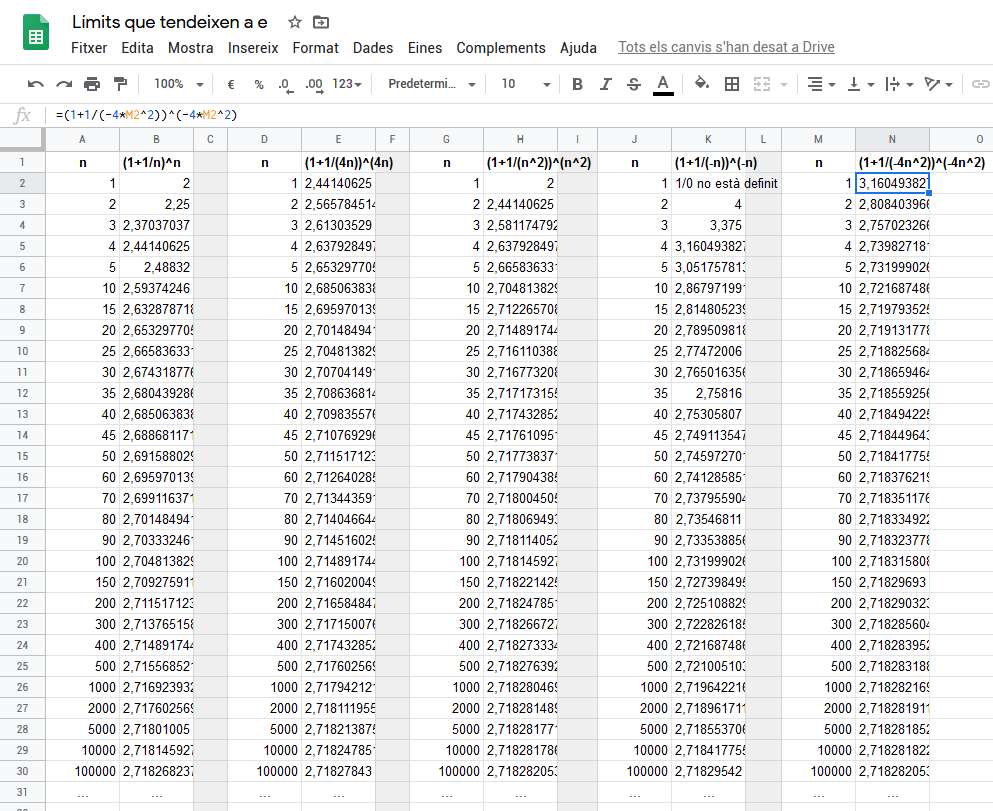 Veiem que totes tendeixen a `e`. Per la qual cosa, podem establir que: Observem vàries coses. Si no haguéssim tot això que acabem d'eplicar aqueste límits serien del tipus: `(1+1/n)^n = (1+1/(+\infty))^(+\infty)=(1+0)^(+\infty)= 1^(+\infty)` `(1+1/-n)^(-n) = (1-1/n)^(-n)(1-1/(+\infty))^(-\infty)=(1+0)^(-\infty)= 1^(-\infty)` Són límits dels que en diem `1^\infty` que tal com hem dit abans són indeteminats (en els dos casos anteriors ja no ho són, ja que els dos límits són `e` tal com acabem de veure). Tot això que acabem de veure ens servirà per treure solucionar aquesta mena d'indeterminació. Com sempre, veurem exemples per veure com funciona la tàctica. Exemple 1 - `lim(1+1/(2n))^n` Casí és un límit com el que acabem d'explicar, `lim(1+1/n)^n`, que seria `e`, però hi ha un `2` que ens fa la guitza. Però si posem un `2` amb l'`n` de l'exponent, però sense fer trampes. Si multipliquem l'`n` de l'exponent per `2`, també ho haurem de dividir per `2`. Si una cosa la multipliquen i dividim pel mateix número, la deixem igual. Si a qualsevol cosa la multiplico per `2/2`, es queda igual.
Doncs ja sabem el truc per calcular límits del tipus `1^\infty` es tracta d'aconseguir que el límit tingui una expresió així, `(1+1/(a_n))^(a_n)`, dintre, de manera que `lim a_n=\pm\infty`. Exemple 2 -`lim((n+1)/(n-2))^n` De bones a primeres això no sembla, ni en pintura, el que acabem de dir sobre el nombre `e`. Però veurem que sí. En primer lloc calculem el límit com hem fet sempre: És un quocient de polinomis elevat a `n`. Els dos polinomis tenen el mateix grau `1`. Per la qual cosa cal dividir els quoeficients, `1/1=1` i això elevat a `n` que se'n va cap a `+\infty`. O sigui: `lim((n+1)/(n-2))^n=1^(+\infty)` Que és un tipus d'indeterminació que haurem de resoldre cercant, per aquí al mig, una expressió del tipus: `(1+1/(a_n))^(a_n)`. Com podem convertir el nostr límit amb una expresió semblant a l'anterior. En primer lloc ens falta un `1` que suma, doncs hi sumem un `1` i hi restem un `1`. Si una cosa li sumes i li restes `1`, es queda igual. i després deixem l' `1` sol i operem elq ue ens queda:
`lim(1+((n+1)-(n-2))/(n-2))^n = lim(1+3/(n-2))^n = ` Que ja s'assembla un xic més al que volem. Tenim un 3 en el numerador que hauria de ser `1`. Per canviar-ho passem el 3 a sota de sota.
Ara ja s'assembla un xic més al que voliem i a sobre `lim (n-2)/3 = +\infty` L'únic que ens falta per tenir-ho perfecte és que en l'exponent també hi hagi,`(n-2)/3`, però això no és problema si a l'exponent, `n` el multipliquem per això i pel seu invers, `(n-2)/3·3/(n-2)` Així, doncs, el nostre límit quedarà:
Si ordenem el producte que hi ha a l'exponent. I recordem fer el pas al revés de què una potència d'una potència és el producte d'exponents `a^(b·c)=(a^b)^c`. `lim(1+1/((n-2)/3))^(n·(n-2)/3·3/(n-2)) = lim(1+1/((n-2)/3))^((n-2)/3·n·3/(n-2)) = lim((1+1/((n-2)/3))^((n-2)/3))^(n·3/(n-2)) =` Perquè lo de dins ja és un límit del tipus, `(1+1/(a_n))^(a_n)`, i l'exponent, `lim(3n)/(n-2)=3`. Ara el que hem de fer és fer exercicis semblants: |