Las múltiples posibilidades de dicho applet permiten al profesor explicar algunos conceptos importantes como por ejemplo:

• MCU: el ángulo girado cada segundo es el mismo, o sea, la velocidad angular es constante. Los intervalos cada 0,1 s nos pueden ser de ayuda.
• MCUA: el ángulo descrito por el objeto cada segundo aumenta (o disminuye) y por tanto la velocidad angular no es constante. Por visualizarlo lo mejor es utilizar los intervalos cada 0,1 s.
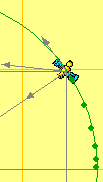
• MVA: El movimiento vibratorio armónico como proyección encima de un eje (x o y) de un movimiento circular uniforme.
• La velocidad y la aceleración angulares pueden no tener el mismo signo: podemos, por ejemplo, visualizar una situación en la que el objeto gira en sentido horario pero acelera en sentido antihorario, o sea primero frena para acabar al final girando en el sentido de la aceleración angular.
• La aceleración centrípeta existe en cualquier movimiento circular (aunque no tenga aceleración angular) y es consecuencia del cambio de dirección de la velocidad. Esta aceleración va variando según la velocidad del objeto en rotación pero su sentido siempre es hacia el centro.
• La aceleración tangencial sólo existe en los movimientos con aceleración angular, o sea en aquéllos en que la velocidad del objeto varía de módulo. Esta aceleración se mantiene constante a lo largo del tiempo y su dirección es tangente a la trayectoria y por tanto paralela a la velocidad. En muchos casos este vector aceleración es difícil de ver porque normalmente ac >> at.
• La aceleración (total) sólo apunta hacia el centro en los MCU. Es interesante observar su descomposición en las componentes tangencial y centrípeta.
• Fuerza centrípeta, tangencial y total. Lo mejor es establecer un paralelismo con las aceleraciones y comprobar que en un MCU sigue habiendo fuerza centrípeta (responsable de la trayectoria circular).
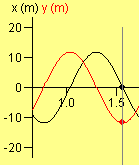
• Las proyecciones de la posición, velocidad, aceleración y fuerza encima de un eje nos permiten estudiar como varían estas magnitudes en un MVA. Es especialmente interesante comentar sus valores en las posiciones extremas. Por ejemplo: cuando la posición es máxima, la velocidad es cero, la aceleración es mínima y la fuerza también.
• La proyección x o y corresponde al mismo tipo de movimiento pero con un desfase de 90º o bien utilizando una función trigonométrica diferente (seno para la proyección vertical y coseno para la horizontal).

Con las configuraciones predeterminadas podemos, de modo gradual, analizar movimientos diferentes: como varía la velocidad, los valores de les aceleraciones, las proyecciones encima de los ejes, las gráficas en función del tiempo...

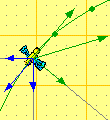
Podemos resolver problemas numéricos y/o ejercicios cualitativos y comprobar su solución con el applet de Movimiento circular. A título de ejemplo:

• Cálculo de la posición angular en un MCU.
• Cálculo de la velocidad angular y de la posición angular en un MRUA.
• Encontrar cuantas vueltas da un objeto que está girando y frena hasta detenerse.
• Calcular la aceleración tangencial, centrípeta y total en un instante de un MCUA.
• Representar cualitativamente los vectores velocidad, aceleración y fuerza en un objeto en rotación.
• Cálculo de la fuerza centrípeta en un MCU y también de la fuerza tangencial y total en un MCUA.
• Representación (cualitativa o cuantitativa) de les gráficas a-t, v-t y x-t (o y-t) en un movimiento circular uniforme.
• Comentar cualitativamente los valores de la fuerza, la aceleración y la velocidad en las posiciones mínima, máxima y nula de un MVA.
• Representación de les gráficas velocidad y aceleración a partir de la gráfica posición - tiempo de un MVA.
  

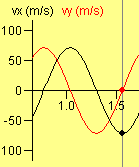
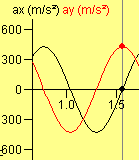
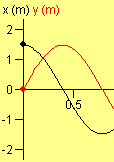
La representación de les gráficas de las proyecciones de la aceleración, la velocidad y la posición en función del tiempo y sus relaciones permite la utilización del applet para mejorar la comprensión del movimiento armónico simple y de los movimientos en general.

Seguramente lo mejor se trabajar primero con sólo una proyección: negra-horizontal o roja-vertical, para comentar entre otros...

• Pendiente v-t = aceleración
• Pendiente x-t = velocidad
• Curvatura x-t = aceleración
• A partir de una de las gráficas podemos representar (cualitativa o cuantitativamente) las otras dos.
• Podemos proponer al alumno elaborar cualitativamente las gráficas a partir de los parámetros de entrada (posición y velocidad angulares iniciales) de un MCU.