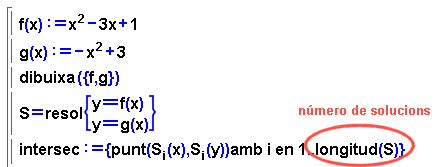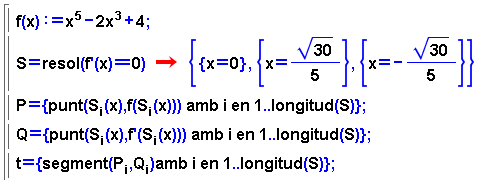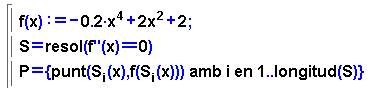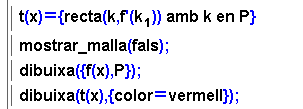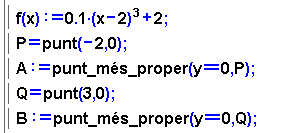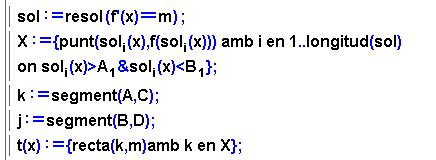|
|
Punts especials en la representació
de funcions |
| |
|
|
|
En aquesta pràctica veureu com calcular i representar
punts d'especial significació de la gràfica d'una funció,
amb una primera consideració sobre la visualització dels
punts d'intersecció de dues funcions.
Tot seguit veureu com es poden presentar les característiques
dels punts singulars o punts d'inflexió, relacionades amb el comportament
de la derivada primera i segona de la funció.
El darrer apartat d'aquesta pràctica, que resumeix
estratègies i recursos vistos en aquesta pràctica i l'anterior,
és una comprovació gràfica i analítica del
teorema del valor mitjà.
|
| |
|
|
|
Representació dels punts d'intersecció
de dues funcions |
| |
|
|
|
Les solucions d'un sistema d'equacions permeten calcular
i visualitzar la intersecció de les gràfiques de dues funcions.
Un cop resolt el sistema i a partir de la llista solució, es defineixen
els punts d'intersecció.
Cal tenir en compte que aquest mètode només serà
útil en el cas que la Wiris pugui trobar totes les solucions
del sistema amb la comanda resol
|
| |
|
 |
|
| |
|
| |
- En la següent finestra activa es defineixen i dibuixen les dues
funcions.
- La comanda resol troba totes les solucions
del sistema en forma de llista.
- El nombre de solucions del sistema s'obté a partir de la longitud
de la llista.
- El conjunt de punts d'intersecció es defineix com una llista
de punts a partir de la llista solució.
- Finalment, es dibuixa el conjunt de punts d'intersecció.
- Canvieu les funcions inicials i observeu els punts de tall.
|
| |
|
|
|
En la finestra d'ampliació teniu una manera
de visualitzar els diferents punts d'intersecció entre dues funcions:
per cada punt d'intersecció s'obre un nou tauler gràfic. |
| |
|
| |
|
|
|
Punts singulars d'una funció |
| |
|
|
|
Per calcular els punts singulars d'una funció, és
a dir, els punts en què el valor numèric de la derivada
és 0, s'ha de resoldre l'equació f'(x) = 0, i després
calcular l'ordenada del punt.
- La comanda resol calcula les solucions de
l'equació; el resultat es dóna en forma d'una taula de
valors: l'anomenem S.
- La comanda longitud dóna el nombre
de solucions de S.
- Cadascuna de les solucions s'obté utilitzant subíndexs.
- Els punts singulars es defineixen com una llista P de punts
a partir de les solucions de l'equació.
- La llista Q són els punts que defineixen els valors
singulars a la funció derivada.
- La llista de segments t serveix per visualitzar millor el gràfic.
|
| |
|
| |
|
| |
|
| |
- La condició perquè un punt singular sigui un mínim
relatiu de la funció, és que la derivada passi de
ser negativa a positiva en aquest punt. A l'inrevés perquè
un punt sigui un màxim relatiu.
- En l'exemple, un dels punts singulars no és ni màxim
ni mínim.
- Si es dibuixen la funció, els punts singulars i la funció
derivada en un mateix gràfic, es comprova la relació entre
les característiques de la funció i el comportament de
la derivada.
|
| |
|
| |
|
| |
|
|
|
- Prepareu una finestra amb les comandes de les dues imatges i comproveu-ne
el resultat. Modifiqueu la funció inicial i executeu la finestra
de la Wiris.
- Feu que es dibuixi la segona derivada en lloc de la primera
per comprovar la relació:
- Si en un punt singular a es verifica que f''(a)>0,
aleshores a és un mínim local
- Si en un punt singular a es verifica que f''(a)<0,
aleshores a és un màxim local.
- Afegiu algun text explicatiu en el tauler gràfic. Vegeu l'exercici
3 d'aquest mòdul.
|
| |
|
|
|
Punts d'inflexió |
| |
|
|
|
De forma similar a com s'ha fet en l'apartat anterior, es
calculen els valors que anul·len la segona derivada i els
punts que aquests valors defineixen a la gràfica de la funció.
|
| |
|
| |
|
| |
|
| |
La condició f''(a) = 0 no garanteix que la funció
presenti un punt d'inflexió per al valor a; cal que
la recta tangent travessi la funció.
Per comprovar gràficament aquest fet, es dibuixa la recta tangent
en els punts en què s'anul·la la segona derivada.
- En aquest cas, s'utilitza la comanda recta(punt,pendent)
que determina la recta per un punt i un pendent donats.
- Les rectes tangents en els punts que anul·len la segona derivada
es defineixen en forma de llista t(x).
|
| |
|
| |
|
| |
|
|
|
- Comproveu que a la gràfica de l'exemple la recta tangent travessa
la funció en els dos punts.
- Busqueu un exemple de funció en què en un punt s'anul·li
la derivada segona i no sigui un punt d'inflexió.
- Representeu els punts d'inflexió d'una funció juntament
amb la segona derivada per comprovar que en aquests punts la segona
derivada presenta un canvi de signe.
- Completeu l'exercici 3 d'aquest mòdul.
|
| |
|
|
|
Teorema del valor mitjà o dels increments
finits |
| |
|
|
|
En aquest apartat es comprovarà el següent teorema:
si f és una funció contínua a l'interval [a,
b] i derivable a (a, b), aleshores hi ha un nombre x
de l'interval (a, b) tal que
f'(x) = (f(b)-f(a)) / (b-a).
La interpretació gràfica del teorema és que en algun
punt de l'interval (a, b) la recta tangent a la funció
f(x) és paral·lela a la recta secant determinada
pels punts imatge dels extrems de l'interval, és a dir, pels punts
(a,f(a)) i (b,f(b)).
A continuació, es descriuen els passos que s'han de seguir per
preparar la finestra de la Wiris corresponent a aquesta activitat, que
podeu obrir amb la icona de l'esquerra.
- Introduir una funció f(x) i dos punts A i B
que determinen l'interval i que es mouen per l'eix d'abscisses.
S'utilitzen la comanda punt_més_proper
i dos punts auxiliars, P i Q, que queden amagats.
|
| |
|
| |
|
| |
|
| |
- Els punts C i D són les imatges a la funció
f(x) dels punts A i B, determinen la recta secant
r de pendent m.
|
| |
|
| |
|
| |
|
| |
- Resoldre l'equació f'(x) = m, el conjunt solució
és una taula que s'anomena sol.
- Les solucions de l'equació determinen una llista de punts X
a la funció. S'imposa que aquests punts estiguin dins l'interval
(A, B)
- Per cada punt de la llista, es defineix la recta tangent a
la funció, s'obté una llista de rectes tangents t(x).
- Les llistes k i j determinen segments auxiliars per
facilitar la comprensió del gràfic.
|
| |
|
| |
|
| |
|
| |
- Finalment, les comandes d'escriptura i dibuix.
|
| |
|
| |
|
| |
|
|
|
- Prepareu una finestra de la Wiris a partir de les imatges anteriors.
- Comproveu que en moure els punts A i B per l'eix d'abscisses
es mostra el punt o els punts que verifiquen la tesi del teorema.
- Executeu la finestra per a altres funcions.
- Introduïu els canvis en la presentació del tauler gràfic
que us semblin adequats.
|
| |
|
| |
|
 |
| |
|
| |
|