L'objectiu d'aquesta pràctica és, com el de totes les d'aquest mòdul, donar idees.

• Donar la idea que la Wiris pot abastar des d'un punt de vista didàctic tots els continguts de les matemàtiques de les etapes d'educació secundària, centrant-nos en aquesta pràctica en el món de la probabilitat.
• Donar-vos idees per al projecte i desenvolupament del treball de fi de curs, no tant pel que fa al contingut curricular, sinó des del punt de vista dels recursos a l'abast per muntar les activitats. En aquest aspecte, torna a ser fonamental l'ús de les llistes.

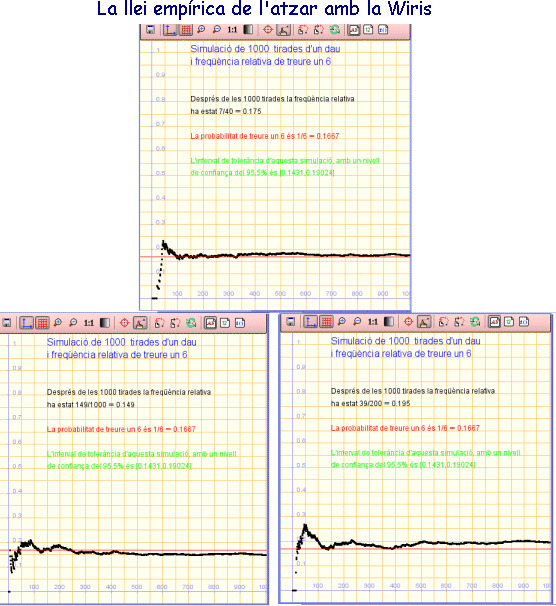
Per a la introducció didàctica del concepte de probabilitat és fonamental poder fer simulacions.

A partir de les simulacions, constatarem el fet que si es fan moltes repeticions d'una experiència aleatòria, la freqüència relativa del nombre d'èxits d'un esdeveniment tendeix a estabilitzar-se entorn a un valor fix: la probabilitat de l'esdeveniment. Aquesta és la llei empírica de l'atzar i, com a empírica que és, només la podrem comprovar amb l'experimentació.

Veurem tot seguit que la Wiris ens pot ajudar també en aquesta tasca.

És clar que per fer simulacions ens cal una taula de nombres aleatoris... o la possibilitat de generar-los amb l'ordinador. Aquest és el cas.

Amb la calculadora Wiris tenim diverses possibilitats de generació de nombres aleatoris seguint una distribució uniforme. La funció aleatori és un exemple de funció que, segons els arguments, retorna una resposta o una altra.

• En aquesta pràctica, fem servir aleatori(n) on n és un nombre natural. Aquesta funció ens retorna un nombre aleatori del recorregut 0..n-1.
• També es pot fer aleatori(m..n)on m i n són nombres enters i la resposta serà un nombre aleatori del recorregut m..n. Podeu observar que 1 + aleatori(n) (opció que s'ha seguit en la pràctica) és equivalent a aleatori(1..n).
• En altres ocasions pot interessar obtenir un nombre aleatori corresponent a una variable contínua. Això també és possible amb la comanda aleatori. Podeu consultar l'índex alfabètic de l'ajuda de la Wiris per veure'n els detalls.

Les primeres línies del codi de l'activitat didàctica que ara podreu analitzar servirien, per elles soles (tot i que després no tenen incidència directa en la llei empírica de l'atzar ni les emprem directament en la pràctica), per constatar quina és la influència de l'atzar en els resultats d'una experiència aleatòria.

• En la primera línia es generen 1000 nombres aleatoris del conjunt {1, 2, 3, 4, 5, 6}. Hem simulat, doncs, 1000 tirades d'un "dau perfecte". Adoneu-vos que elnombre de tirades en cada simulació el podrem variar donar canviar el valor de la variable n.
• En la segona línia la comanda compta_element ens permet elaborar la taula de freqüències dels resultats que s'han observat.
• Com que el resultat de compta_element (un divisor) s'ha assignat a una variable, en la tercera línia veiem com es pot fer per obtenir el recompte del nombre de sisos que han sortit.

Com sempre podeu accedir a la pràctica totalment elaborada. Però ara de moment pot se rinteressant que escriviu les tres línies que s'han comentat i repetiu diverses vegades el càlcul; així veureu les diferències que s'observen d'una vegada a l'altra i la influència de l'atzar en les simulacions.

Per fer visual la llei empírica de l'atzar, haurem de repetir un procediment com el que acabem de comentar, però no per al total de tirades sinó per cada nombre de tirades, i haurem d'observar què passa (i ho farem mitjançant la generació d'un gràfic) quan aquest nombre de tirades va augmentant.

Com en altres ocasions, ara us proposem primer de tot que feu l'activitat i després ja n'analitzarem el codi. Cliqueu a la icona de pantalla activa que teniu a l'esquerra (on s'obre automàticament el tauler gràfic) i repetiu l'experimentació algunes vegades per veure novament les diferències d'una simulació a una altra. Veureu que si treballeu en línia heu d'esperar uns segons perquè s'acabi el càlcul; però per si voleu treballar amb la WirisDesktop us podeu baixar l'activitat en un fitxer comprimit amb l'altra icona de l'esquerra.

• Recordeu que per repetir l'activitat no cal que tanqueu el tauler on s'ha mostrat el gràfic (però segurament és més clar fer-ho); heu de posar el cursor en una de les línies que tenen el codi de l'activitat i fer clic a la icona d'execució (o també Control + Retorn). (Eventualment, si treballeu en línia, també podeu actualitzat la pàgina HTML)

Vegem el codi que ha permès fer l'activitat anterior.

Ja hem comentat que les primeres línies generen n tirades d'un dau i compten quants sisos han sortit. Però no ens interessa veure-ho en el total de les 200 tirades, sinó per cada nombre de tirades de l'1 al n.

Això es podria fer amb la comanda compta_element aplicada per cada nombre de tirades, mitjançant una sentència per.. en però d'aquesta manera el càlcul és molt repetitiu i laboriós i fins i tot la Wiris Desktop diu "que no pot acabar el càlcul per falta de temps" per poc gran que sigui n. Com a alternativa proposem unes sentències de programació per anar fent el compte element a element a partir de la llista LL de tirades.

Construïm dues llistes, una, nsis, que dóna el nombre de sisos que han sortit fins aquell moment (i tirades) i l'altra, Frel que en el lloc i hi té la freqüència relativa dels sisos que han sortit en les i primeres tirades.

• En el primer lloc de cada llista hi posem un 1 si la primera tirada és un 6 o un 0 en cas contrari.
• En cada lloc de la llista nsis hi posem el valor anterior més 1 si ha sortit un sis o bé hi deixem el mateix valor anterior si no ha sortit un 6.
• La llista Frel la construïm a partir de la definició de freqüència relativa. Podeu llegir un comentari sobre la conveniència o no de fer escriure aquestes llistes.

El següent pas serà fer el dibuix; es comença per definir el tauler i es construeix una llista de punts per fer el gràfic. Segur que interpreteu adequadament aquestes línies de comandes:

• Vegeu que no es canvia la mida de la finestra: serà de 450 x 450, com és habitual.
• S'estableix que l'eix de les x abasti una graduació d'unes quantes unitats més de la n. Semblantment amb l'eix de les y: els valors observats varien de 0 a 1, però es dóna una mica de marge.
• Es defineix el centre del tauler perquè el gràfic quedi situat com ja heu vist en l'exercitació de l'activitat.
• Es construeix la llista graf de punts que volem dibuixar. Fixeu-vos que, com que Frel és una llista, Frel_i és l'element de lloc i en aquesta llista. No seria vàlida la notació Frel(i) com si treballéssim amb una funció.
• Tot seguit, es dibuixa la gràfica i també es dibuixa la recta que mostra l'estabilització de la Frel entorn del valor de la probabilitat...

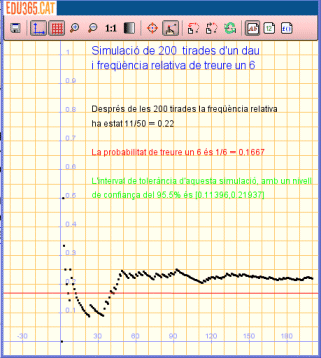
...O potser no la mostra en alguna simulació? És clar que no, tot depèn de l'atzar!

Aquesta és "la gràcia" de fer aquest tipus d'activitats amb alumnes, que entenguin per una banda la llei empírica de l'atzar però per una altra coneguin la variabilitat dels resultats estadístics.

Aquesta variabilitat és més gran com més menut és el nombre de repticions que es fa en la simulació, com podeu comprovar si canvieu en la primera línia de codi 1000 per 200, per exemple: 200 tirades són "molt poques" per constatar la llei empírica de l'atzar.

Per si es vol aprofitar aquesta idea gràfica per introduir el concepte d'interval de tolerància/de confiança, s'han incorporat unes informacions a la pantalla gràfica. Proveu de repetir l'experimentació, observeu la variabilitat i veureu que sovint (poc més o menys una de cada 20 vegades) tot i que la tria aleatòria s'ha fet correctament, el resultat queda fora d'aquest interval. Aquesta idea l'haurien de donar amb molta més insistència els elaboradors d'enquestes!

Si engegueu l'activitat següent de la manera habitual, podreu fer algunes reflexions de caràcter didàctic sobre la distribució normal a partir d'una gràfica inicial, que és justament la de la funció de densitat de probabilitat de la distribució normal estàndard.

• Tal com s'indica a la imatge, si moveu els punts negres que determinen un segment a la part inferior del tauler gràfic, podreu variar la mitjana (indicada per l'eix de simetria, recta de color verd) i la desviació estàndard de la distribució, i la gràfica s'actualitzarà.
• Si moveu els dos punts vermells que teniu sobre l'eix de les x, canviareu l'interval de què es calcula la probabilitat. Ja sabeu que aquesta probabilitat és l'àrea de la zona acolorida de color vermell.

Experimenteu-hi!

Us recordem que podeu ampliar manualment la part visible de la finestra. Pot ser interessant que en aquest cas ho feu amb l'eix horitzontal per a algunes de les activitats que us aconsellem:

• Comparació de gràfiques amb la mateixa mitjana i diferents desviacions estàndards.
• Comparació de gràfiques amb la mateixa desviació estàndard i diferents mitjanes.
• Amb la gràfica de la normal estàndard: visualització de la probabilitat dels intervals [-1, 1], [-2, 2] i [-3, 3] que s'acostumen a considerar característics de la distribució normal.
• Idea de l'estandardització: vegeu que la probabilitat de l'interval [0,5; 1,5] amb la distribució normal estàndard és la mateixa que la probabilitat de l'interval [1,5; 3,5] en la distribució normal que té mitjana 0,5 i desviació estàndard 2. Els valors 1,5 i 3,5 són, en aquest cas, els que disten de la mitjana, respectivament 0,5 i 1,5 desviacions estàndards. Per això es corresponen amb els valors 0,5 i 1,5 de la normal estàndard.

A continuació, es comenten alguns aspectes del codi amb què s'ha preparat l'activitat. El podreu consultar fàcilment si engegueu i tanqueu el tauler gràfic.

• La funció que defineix la densitat de probabilitat de la distribució normal és:
  
  
• Les primeres línies del codi es destinen a definir la interactuació que es pot fer per definir els valors de la mitjana i la desviació estàndard, juntament amb la recta que serà l'eix de simetria de la corba. Tot i que es podria fer amb desplaçadors en aquesta ocasió hem optat per fer-ho amb punt_més_proper perquè així es veu amb les distàncies reals, sobre el gràfic.
  
  
• Hem posat expressament una línia per comentar "que no fa el que sembla". Segur que quan heu estat fent experimentacions i heu variat els paràmetres definidors de la distribució normal, heu pensat en la possibilitat que el centre del tauler s'actualitzés. Això no és possible, perquè el tauler només es defineix la primera vegada que es processa la comanda tauler. Així, doncs, com que
  
  es llegeix (per primera vegada) en un moment en què m = 0 i s = 1 és equivalent a
  
  El tauler es veu tota l'estona amb aquest centre, encara que manualment canviem l'amplada de la finestra. Recordeu, doncs: el tauler es defineix d'una vegada per totes i no es pot actualitzar.
  
  
• La construcció de la llista dels segments que acoloreixen l'àrea que ens dóna la probabilitat de l'interval [xm, xn] es fa així:
  
  • Si es volgués que l'àrea quedés completament acolorida, es podria substituir el 0,05 per un nombre més petit, per exmeple, 0,01, però llavors costaria froça actualitzar el dibuix. Proveu-ho i considereu si us sembla un valor afegit.
  • S'afegeix el segment que tanca per la part dreta, perquè si no es fes així, potser el salt de 0,05 faria que no es passés exactament per xn i llavors l'efecte visual no seria correcte.
    
    

• Potser us heu adonat que quan s'executa la finestra de la Wiris que inclou aquesta activitat, surt un missatge d'avís (indicat per un requadre verd). Per què?

  Quan una pantalla de la Wiris s'ha gravat sense la barra d'eines (com és el cas), tampoc mostra la finestra d'errors. Però amb el botó dret del ratolí, podeu recuperar-les en posició flotant. Si ho feu, llegireu de què us vol avisar el programa:

  

  Efectivament, els valors de la probabilitat d'un interval segons la distribució normal de probabilitat s'han de fer per integració numèrica!
  
  És, justament, la integral  la que ens dóna aquesta probabilitat.

• Ben segur que entendreu tot allò que no es comenta. Si no fos així, ja sabeu que podeu preguntar-ho!