|
MOVIMENTS DIRECTES
El moviment de les figures es deriva del moviment dels punts i de les relacions d’igualtat. En aquesta pràctica s’analitzen els moviments directes.
|
||||||||
 |
Activitats
Dues figures planes són directament iguals quan una d’elles
pot desplaçar-se sense sortir del pla fins superposar-se a l’altra.
Aquest concepte ja s’ha vist a la pràctica
4 del mòdul 2. Els punts, angles o segments que se superposen
s’anomenen elements homòlegs de les dues figures. La transformació
del pla que assigna una figura a l’altra és un moviment directe.
2. La translació Obriu la figura TRANS1. Desplaceu el triangle verd fins superposar-lo al triangle groc. Torneu-los a separar i traceu els segments que uneixen els vèrtexs homòlegs. 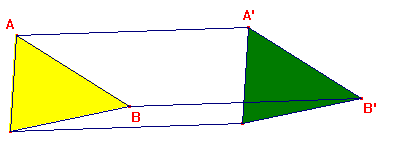
Per tant, en una translació els segments homòlegs són iguals i paral·lels, i els angles homòlegs són iguals. Res més senzill que traslladar un objecte amb el Cabri: és la funció del punter Comproveu que trasllada triangles, polígons, circumferències, segments i arcs. Ara bé, aquest translació no permet comparar l'objecte inicial i l'objecte transformat, ni construir aquest a partir del primer deixant-lo present a la figura. Aquesta funció està atribuïda a l'eina Translació del grup Transformacions. El funcionament d'aquesta eina deriva de la propietat fonamental:
El Cabri requereix la presència d'aquest parell de punts mitjançant un vector. Podeu crear un vector amb l'eina Vector del grup Rectes. Un cop el tingueu, podeu traslladar de tot. Per practicar, obriu la figura TRANS2.FIG i traslladeu d'acord amb el vector donat tots els objectes presents a la figura. Cal que feu clic primer a l'objecte i després al vector. La construcció euclidiana (amb regle i compàs) d'una translació
no requereix cap vector, i sí una bona quantitat de rectes paral·leles.
Feu-la com a Exercici 1
2. El gir Obriu la figura GIR1. Desplaceu el triangle verd fins superposar-lo al triangle gris. Teniu per fer-ho dues eines del grup Punter: Després torneu-los a separar. El pas d'un triangle a l'altre és un moviment directe anomenat gir. Anomeneu A, B i C als vèrtexs d'un triangle i A', B' i C' als
seus homòlegs de l'altre. Traceu les mediatrius de AA', BB' i CC'
i veureu que són concurrents en un punt O que s'anomena el centre
de gir.
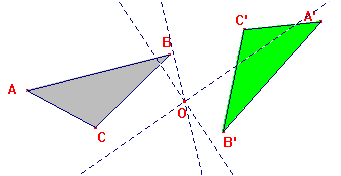 Posteriorment traceu els angles amb vèrtex O i tals que els seus costats passen per dos punts homòlegs. Mesureu-los. El valor comú de tots aquests angles és l’angle del gir. Observareu la propietat que defineix els girs:
Per efectuar un gir amb Cabri disposeu de l'eina Rotació del grup Transformacions. El funcionament d'aquesta eina deriva de la propietat fonamental:
El Cabri requereix la presència de l'angle de gir mitjançant el valor numèric de la seva mesura. Podeu crear un valor numèric amb l'eina Edició numèrica del grup Aspecte. Activeu-la i escriviu en el quadre el valor que vulgueu i que serà l'angle de gir en graus.
Un cop tingueu el centre i aquest valor numèric, podeu girar de tot. Per practicar, obriu la figura GIR2.FIG i gireu d'acord amb l'angle donat al voltant del centre O tots els objectes presents a la figura. Cal que feu clic primer a l'objecte, després a l'angle i finalment al centre. La construcció euclidiana (amb regle i compàs) d'un gir
no requereix cap valor numèric, i sí un angle físicament
present. Feu-la com a Exercici 2
3. Els moviments directes En l’exercici 2 haureu comprovat que per girar una figura poligonal
només cal girar dos punts. A partir d’aquí, tots els altres
vèrtexs s’obtenen traslladant els angles de la figura original,
sense que l’angle de gir torni a intervenir. És per això
que
Per tant, donats dos segments iguals no paral·lels hi ha un gir
que transforma l’un en l’altre; si els dos segments són iguals i
paral·lels, hi ha una translació que transforma l’un en l’altre.
Per això
4. La composició de moviments La realització successiva de dos moviments del mateix objecte és la seva composició. Com que la composició de dos moviments directes és un altre moviment directe només pot ser una translació o un gir. És bastant obvi que la composició de dues translacions és una translació, però si ho voleu feu-vos una figura que ho demostri. Obriu la figura COMPGIR1, que mostra la composició de dos girs del mateix centre. El primer porta ABC a A'B'C' i el segon porta A'B'C' a A"B"C". 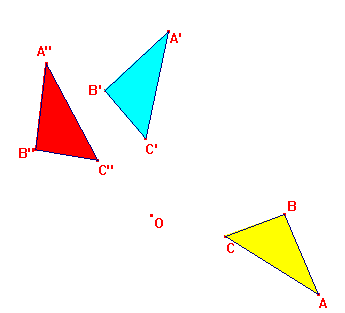 Penseu quina transformació passa d'ABC a A''B''C'' i veureu que és un gir. Té el mateix centre que els altres dos? Quant val el seu angle de gir? Responeu aquestes preguntes pel vostre compte. Quant a la composició de dos girs de diferent centre, estudieu-la de forma semblant a l’Exercici 3 Finalment, la composició d’un gir i d’una translació serà
objecte de l’ Exercici 4
Resum
|